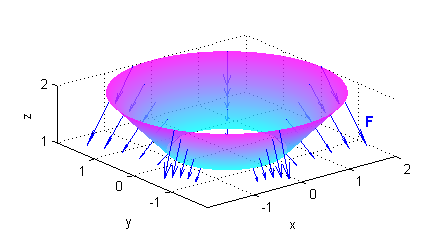
Utilizamos la fórmula $$\mbox{Flujo}=\int\!\! \int_R (-M f'_x-Nf'_y+P)\, dA$$ donde \(M\), \(N\) y \(P\) son las componentes del campo evaluadas sobre la superficie y \(R\) es la proyección en el plano XY. En este caso $$-M f'_x-Nf'_y+P=-\frac{x^2}{\sqrt{x^2+y^2}}-\frac{y^2}{\sqrt{x^2+y^2}}-(x^2+y^2)=-\sqrt{x^2+y^2}-(x^2+y^2)$$ Así, $$\mbox{Flujo}=-\int\!\! \int_R \left(\sqrt{x^2+y^2}+(x^2+y^2) \right)\, dA$$ que en polares es $$\mbox{Flujo}=-\int_0^{2\pi} \int_1^2 r(r+r^2 )\, dr\, d\theta$$ Sin necesidad de calcular esa integral, observamos que el resultado va a ser un número negativo. Sin embargo es evidente que el campo vectorial apunta hacia abajo en toda la superficie, por lo que el flujo debería haber resultado positivo. ¿Dónde está el error? Analízalo y pulsa en 'Continuar'.
Continuar

En la fórmula utilizada para el flujo se está tomando la normal a la superficie que apunta hacia arriba: $${\bf N}= -f'_x\, {\bf i}-f'_y\,{\bf j}+{\bf k}$$ luego el flujo calculado es hacia arriba, y por tanto opuesto al pedido en el enunciado. El flujo correcto es $$\mbox{Flujo}=\int_0^{2\pi} \int_1^2 r(r+r^2 )\, dr\, d\theta= 2\pi\left[\frac{1}{3}r^3+\frac{1}{4}r^4\right]_1^2=\frac{73}{6}\pi$$