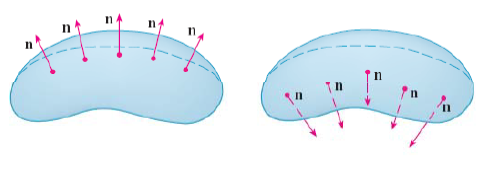
Supondremos que la superficie S tiene un plano tangente en cada punto de S (excepto en cualquiera de los puntos frontera). Como sabemos existen dos vectores normales unitarios en cada punto.

Si en cada punto de S es posible definir un vector unitario normal $\bf{n}$ que variase de manera continua sobre S entonces diremos que S es una superficie orientada yl la elección de n proporcionaría una orientación de S. Existen dos orientaciones para cualquier superficie.

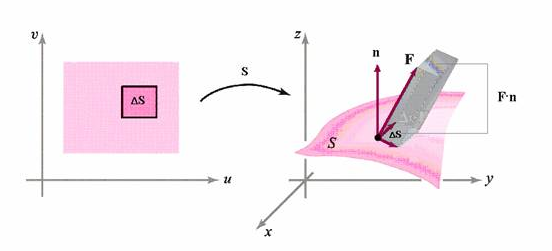
Los dos elementos que intervienen en la integral de un campo vectorial sobre una superficie son:
$\;\;\;\;\; \bullet$ La superficie orientada $S$, en las mismas condiciones de continuidad y derivabilidad impuestas para definir la integral de un campo escalar sobre ella; llamaremos ${\bf n}$ a la normal unitaria.
$\;\;\;\;\; \bullet$ El campo vectorial ${\bf F}(x,y,z)$ definido en una región del plano que contenga a $S$ de forma que tomado sobre los puntos de $S$ el resultado sea continuo: la función compuesta por el campo sobre la superficie es una función vectorial de tres componentes, cada una es una función real de dos variables, que debe ser continua.
La integral del campo F sobre la superficie $S$ es la integral del campo escalar ${\bf F}\cdot{\bf n}$: \begin{equation}\label{t5e3}\int \int_S {\bf F}\cdot{\bf n} \, dS\end{equation}
Expresión para explícitas
Si el campo es ${\bf F}=(M,N,P)$ y la superficie viene dada por $z=f(x,y)$ en $R$, la integral de ${\bf F}$ sobre $S$ se puede expresar como $$\int \int_S {\bf F}\cdot{\bf n} \, dS=\int \int_S (-Mf'_x-Nf'_y+P)\, dA$$ si ${\bf n}$ apunta hacia arriba y como $$\int \int_S {\bf F}\cdot{\bf n} \, dS=\int \int_S (Mf'_x+Nf'_y-P)\, dA$$ si ${\bf n}$ apunta hacia abajo.
