Ejercicios preliminares e instantáneos. Integral de superficie

Ejercicio 1

Halla el vector normal ${\bf N}(x,y)=(-f'_x(x,y),-f'_y(x,y),1)$, esto es el vector normal de tercera componente positiva, para las superficies y coordenadas $(x,y)=(x_0,y_0)$ indicadas. En cada caso, representa una porción de superficie que incluya al punto $(x_0,y_0,f(x_0,y_0))$ y dibuja el vector ${\bf N}(x_0,y_0)$ sobre él.
  1. $z=f(x,y)=2-3y$, $(x_0,y_0)=(0,0)$;
  2. $z=f(x,y)=\sqrt{4-x^2}$, $(x_0,y_0)=(1,0)$;
  3. $z=f(x,y)=1+x^2+y^2$, $(x_0,y_0)=(0,1)$;
  4. $z=f(x,y)=\sqrt{4-x^2-y^2}$, $(x_0,y_0)=(0,-1)$;
  5. $z=f(x,y)=2-\sqrt{x^2+y^2}$, $(x_0,y_0)=(3,0)$;
  6. $z=f(x,y)=y^2$, $(x_0,y_0)=(2,2)$.
Solución caso a.
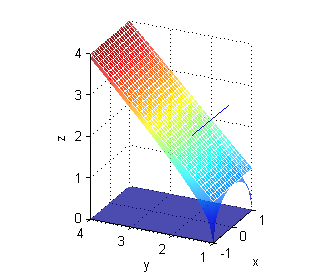
$z=f(x,y)=2-3y$ es un plano, el vector normal es ${\bf N}=(0,3,1)$ en todos los puntos: Gráfica
Podemos hacer este dibujo a mano. Para hacerlo en el ordenador podemos poner: 
	 [X,Y]=meshgrid(-1:1);
	 surf(X,Y,2-3*Y)
	 shading interp
	 hold on
	 quiver3(0,0,2,0,3,1)
	 hold off
	 alpha(.7)
	 axis equal
	 xlabel('x');ylabel('y');zlabel('z')
b. $z=f(x,y)=\sqrt{4-x^2}$, $(x_0,y_0)=(1,0)$
Solución caso b.
$z=f(x,y)=\sqrt{4-x^2}$ es un cilindro parabólico; el vector normal en cada punto es ${\bf N}=(\frac{x}{\sqrt{4-x^2}},0,1)$; en el punto $(1,0,\sqrt{3})$ es ${\bf N}=(\frac{1}{\sqrt{3}},0,1)$:
Gráfica
Podemos hacer este dibujo a mano. Para hacerlo en el ordenador podemos poner: 
	[X,Y]=meshgrid(0:.1:2,-1:1);
	surf(X,Y,sqrt(4-X.^2))
	shading interp
	hold on
	quiver3(1,0,sqrt(3),1/sqrt(3),0,1)
	hold off
	alpha(.7)
	axis equal
	xlabel('x');ylabel('y');zlabel('z')
c. $z=f(x,y)=1+x^2+y^2$, $(x_0,y_0)=(0,1)$
Solución caso c.
$z=f(x,y)=1+x^2+y^2$ es un paraboloide; el vector normal en cada punto es ${\bf N}=(-2x,-2y,1)$; en el punto $(0,1,2)$ es ${\bf N}=(0,-2,1)$:
Gráfica
Podemos hacer este dibujo a mano. Para hacerlo en el ordenador podemos poner: 
	[X,Y]=meshgrid(-1:.1:1,0:.1:2);
	surf(X,Y,1+X.^2+Y.^2)
	shading interp
	hold on
	quiver3(0,1,2,0,-2,1)
	hold off
	alpha(.7)
	axis equal
	xlabel('x');ylabel('y');zlabel('z')
d. $z=f(x,y)=\sqrt{4-x^2-y^2}$, $(x_0,y_0)=(0,-1)$
Solución caso d.
$z=f(x,y)=\sqrt{4-x^2-y^2}$ es una semiesfera (aquí dibujamos sólo una porción); el vector normal en cada punto es ${\bf N}=(\frac{x}{\sqrt{4-x^2-y^2}},\frac{y}{\sqrt{4-x^2-y^2}},1)$; en el punto $(0,-1,\sqrt{3})$ es ${\bf N}=(0,\frac{-1}{\sqrt{3}},1)$:
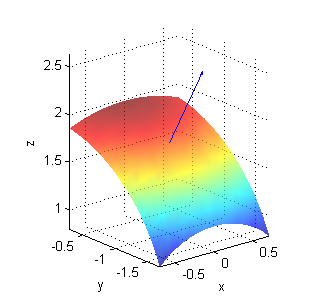
Gráfica
Podemos hacer este dibujo a mano. Para hacerlo en el ordenador podemos poner: 
		  	[X,Y]=meshgrid(-.7:.1:.7,-1.7:.1:0-.3);
		  	surf(X,Y,sqrt(4-(X.^2+Y.^2)))
		  	shading interp
		  	hold on
		  	quiver3(0,-1,sqrt(3),0,-1/sqrt(3),1)
		  	hold off
		  	alpha(.7)
		  	axis equal
		  	xlabel('x');ylabel('y');zlabel('z')
e. $z=f(x,y)=2-\sqrt{x^2+y^2}$, $(x_0,y_0)=(3,0)$
Solución caso e.
$z=f(x,y)=2-\sqrt{x^2+y^2}$ es un semicono; el vector normal en cada punto es ${\bf N}=(\frac{x}{\sqrt{x^2+y^2}},\frac{y}{\sqrt{x^2+y^2}},1)$; en el punto $(3,0,-1)$ es ${\bf N}=(1,0,1)$
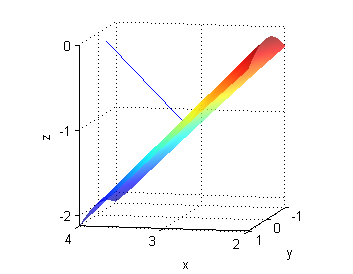
Gráfica
Podemos hacer este dibujo a mano. Para hacerlo en el ordenador podemos poner: 
		   	[X,Y]=meshgrid(2:.1:4,-1:.1:1);
		   	surf(X,Y,2-sqrt(X.^2+Y.^2))
		   	shading interp
		   	hold on
		   	quiver3(3,0,-1,1,0,1)
		   	hold off
		   	alpha(.7)
		   	axis equal
		   	xlabel('x');ylabel('y');zlabel('z')
f. $z=f(x,y)=y^2$, $(x_0,y_0)=(2,2)$
Solución caso f.
$z=f(x,y)=y^2$ es un cilindro parabólico; el vector normal en cada punto es ${\bf N}=(0,-2y,1)$; en el punto $(2,2,4)$ es ${\bf N}=(0,-4,1)$:
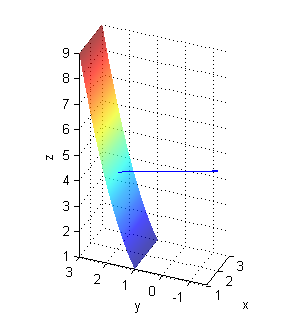
Gráfica
Podemos hacer este dibujo a mano. Para hacerlo en el ordenador podemos poner: 
		   	[X,Y]=meshgrid(1:3,1:.1:3);
		   	surf(X,Y,Y.^2)
		   	shading interp
		   	hold on
		   	quiver3(2,2,4,0,-4,1)
		   	hold off
		   	alpha(.7)
		   	axis equal
		   	xlabel('x');ylabel('y');zlabel('z')

Ejercicio 2

El área de la porción de plano tangente a $z=f(x,y)$ en el punto $P_0(x_0,y_0,f(x_0,y_0))$ que se proyecta en el rectángulo $R$ es igual a $|{\bf N}|\mbox{área}(R)$, donde ${\bf N}$ es el vector normal a la superficie en el punto $P_0$. Encuentra ese área para
  1. $z=f(x,y)=-x^2$, $R=[-1,1]\times[0,2]$, $(x_0,y_0)=(0,1)$;
  2. $z=f(x,y)=\sqrt{y^2-x^2}$, $R=[-1,1]\times[1,4]$, $(x_0,y_0)=(0,2)$.
Ejemplo
Solución
Si los datos fueran $z=f(x,y)=x^2+y^2$, $R=[0,1]\times[0,2]$ y $(x_0,y_0)=(0,0)$, el vector normal sería ${\bf N}=(0,0,1)$ y $\mbox{área}(R)=2$, con lo cual el área de la porción de plano tangente a $z=f(x,y)=x^2+y^2$ en el punto $P_0(0,0,0)$ resultaría $|{\bf N}|\mbox{área}(R)=2$
  1. el vector normal en cada punto es ${\bf N}=(2x,0,1)$, luego en el punto $(0,1,0)$ es ${\bf N}=(0,0,1)$ y $|{\bf N}|=1$; puesto que $\mbox{área}(R)=4$, el área de la porción de plano tangente es también 4
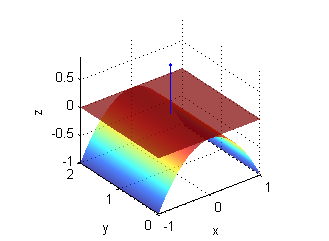
    Gráfica
  2. el vector normal en cada punto es ${\bf N}=(\frac{x}{\sqrt{y^2-x^2}},\frac{-y}{\sqrt{y^2-x^2}},1)$, luego en el punto $(0,2,2)$ es ${\bf N}=(0,-1,1)$ y $|{\bf N}|=\sqrt{2}$ ; puesto que $\mbox{área}(R)=6$, el área de la porción de plano tangente es $6\sqrt{2}$
    Gráfica

Ejercicio 3

Para cada una de las siguientes superficies cerradas, analiza en qué puntos el vector normal con tercera componente positiva apunta hacia dentro de la superficie:
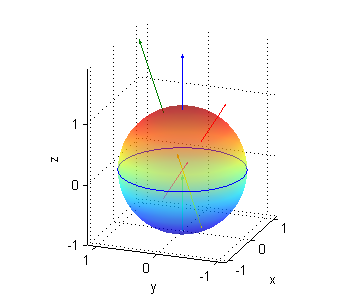
  1. esfera $x^2+y^2+z^2=1$
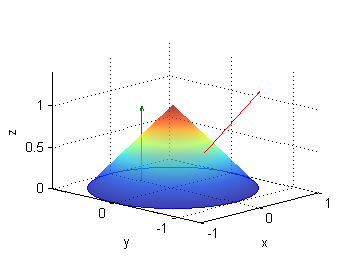
  2. superficie unión del disco de radio 1 y centro $(0,0,0)$ en el plano $z=0$ con la porción de $z=1-\sqrt{x^2+y^2}$ en $z>0$;
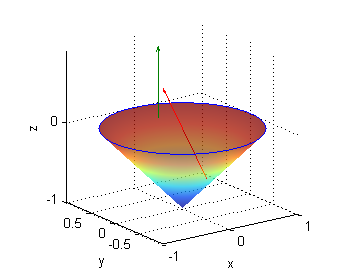
  3. superficie unión del disco de radio 1 y centro $(0,0,0)$ en el plano $z=0$ con la porción de $z=\sqrt{x^2+y^2}-1$ en $z>0$.
Pista
Solución
En cada punto de una superficie suave de dos caras u orientable existen dos sentidos posibles para la dirección normal; si la superficie responde a una ecuación del tipo $z=f(x,y)$ o es unión de varias de éstas, fijar un sentido para la normal equivale a fijar el signo de la tercera componente.
  1. en los puntos de la semiesfera inferior, $z=-\sqrt{1-x^2-y^2}$
    Gráfica
  2. en los puntos del disco, no en los del cono
    Gráfica
  3. en los puntos del cono, no en los del disco
    Gráfica

Ejercicio 4

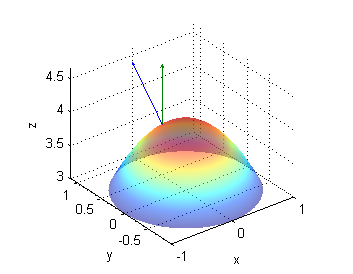
Calcula el ángulo $\gamma$, comprendido entre 0 y $\frac{\pi}{2}$, formado por los vectores ${\bf n}=\frac{{\bf N}}{|{\bf N}|}$ y ${\bf k}$, para la superficie $z=4-x^2-y^2$ en los puntos
  1. $A(0,0,4)$
  2. $B(\frac{1}{2\sqrt{3}},0,\frac{47}{12})$
  3. $C(0,\frac{1}{2},\frac{15}{4})$
Pista
Solución
Recuerda que el ángulo $\gamma$ formado entre dos vectores ${\bf u}$ y ${\bf v}$ puede calcularse haciendo su producto escalar, ya que $${\bf u}\cdot{\bf v}=|{\bf u}||{\bf v}|\cos(\gamma)$$
El vector unitario en cada punto es ${\bf n}=\frac{(2x,2y,1)}{\sqrt{4(x^2+y^2)+1}}$ luego $$\gamma =\mbox{arccos}({\bf n}\cdot{\bf k})=\frac{1}{\sqrt{4(x^2+y^2)+1}}$$
  1. ángulo entre el vector ${\bf n}$ y ${\bf k}$ en $A$: $\gamma=\mbox{arccos}(1)=0$
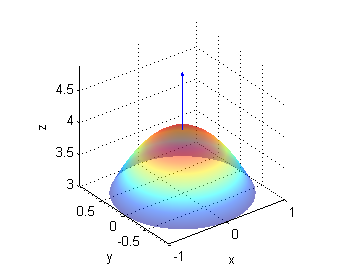
    Gráfica
  2. ángulo entre el vector ${\bf n}$ y ${\bf k}$ en $B$: $\gamma=\mbox{arccos}(\frac{\sqrt{3}}{2})=\frac{\pi}{6}$
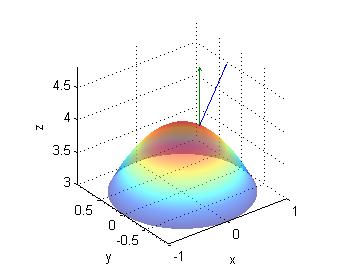
    Gráfica
  3. ángulo entre el vector ${\bf n}$ y ${\bf k}$ en $C$: $\gamma=\mbox{arccos}(\frac{1}{\sqrt{2}})=\frac{\pi}{4}$
    Gráfica

Ejercicio 5

Escribe la expresión de la composición $g(x,y,f(x,y))$ para $g(x,y,z)=x^2+y^2+z^2$ siendo $z=f(x,y)$ cada una de las siguientes:
  1. $z=f(x,y)=2-3y$;
  2. $z=f(x,y)=\sqrt{4-x^2}$;
  3. $z=f(x,y)=1+x^2+y^2$;
  4. $z=f(x,y)=\sqrt{4-x^2-y^2}$;
  5. $z=f(x,y)=2-\sqrt{x^2+y^2}$;
  6. $z=f(x,y)=y^2$.
Comentario
Solución
$z=f(x,y)$ podría ser la ecuación de una superficie y $g(x,y,z)$ el valor de un campo escalar, como la temperatura o la densidad de masa superficial, en cada punto de esa superficie.
  1. $u(x,y)=x^2+y^2+(2-3y)^2$
  2. $u(x,y)=4+y^2$
  3. $u(x,y)=x^2+y^2+(1+x^2+y^2)^2$
  4. $u(x,y)=4$
  5. $u(x,y)=2(x^2+y^2-2\sqrt{x^2+y^2}+2)$
  6. $u(x,y)=x^2+y^2(1+y^2)$

Ejercicio 6

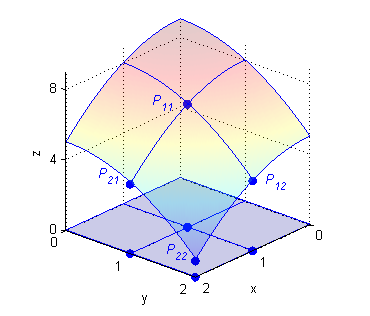
Dibuja la porción $S$ de $z=9-x^2-y^2$ que se proyecta sobre $R=[0,2]\times [0,2]$. Dibuja en $R$ los cuatro subrectángulos $$R_{11}=[0,1]\times [0,1] \ ,\ \ R_{12}=[0,1]\times [1,2] \ ,\ \ R_{21}=[1,2]\times [0,1] \ ,\ \ R_{22}=[1,2]\times [1,2]$$ Dibuja en $S$ los cuatro parches correspondientes a estos subrectángulos. En cada uno de los $R_{ij}$ marca el punto correspondiente a las coordenadas $x$ e $y$ máximas. Llamaremos $P_{ij}$ a los puntos en la superficie $S$ que se corresponden con esos puntos que has marcado en $R$. Encuentra y dibuja los cuatro puntos $P_{ij}$.
Pista
Solución
El punto de $R_{11}=[0,1]\times [0,1]$ de coordenadas $x$ e $y$ máximas es $(1,1)$; por tanto el punto correspondiente a $R_{11}$ es $P_{11}=(1,1,7)$.
Los puntos son $P_{11}=(1,1,7)$, $P_{12}=(1,2,4)$, $P_{21}=(2,1,4)$ y $P_{22}=(2,2,1)$:
Gráfica

Ejercicio 7

En el ejercicio anterior dividimos el rectángulo $R=[0,2]\times [0,2]$ en los cuatro subrectángulos $$R_{11}=[0,1]\times [0,1] \ ,\ \ R_{12}=[0,1]\times [1,2] \ ,\ \ R_{21}=[1,2]\times [0,1] \ ,\ \ R_{22}=[1,2]\times [1,2]$$ y dibujamos sobre $S$ (que es la parte de $z=9-x^2-y^2$ que se proyecta sobre $R$) los correspondientes cuatro parches. En cada uno de estos parches tomamos el punto $P_{ij}$ correspondiente a las coordenadas $x$ e $y$ máximas.

Halla el vector normal en los puntos $P_{ij}$, evalúa los cuatro productos $|{\bf N}|\mbox{área}(R_{ij})$ y súmalos. Esa suma es una aproximación (poco precisa, pues sólo tomamos cuatro subrectángulos de $R$) del área de $S$.

Solución
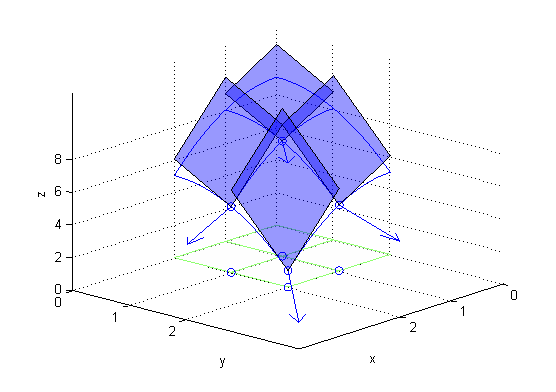
Para todos los puntos, $|{\bf N}|=\sqrt{1+4(x^2+y^2)}$, luego los módulos de las normales en los puntos $P_{ij}$ son $$|{\bf N}(P_{11})|=3 \ \ ,\ \ |{\bf N}(P_{12})|=\sqrt{21}\ \ ,\ \ |{\bf N}(P_{21})|=\sqrt{21}\ \ ,\ \ |{\bf N}(P_{22})|=\sqrt{33}$$ Puesto que el área de cada rectángulo $R_{ij}$ es 1, la suma pedida es $$3+2\sqrt{21}+\sqrt{33}\approx 17.09$$ Gráfica
El área que se obtiene realizando la integral con Matlab resulta 13.0046: $$\mbox{área}=\int_0^2\!\! \int_0^2\sqrt{4(x^2+y^2)+1}\, dx\, dy\approx 13.0046$$

Ejercicio 8

En los ejercicios anteriores dividimos el rectángulo $R=[0,2]\times [0,2]$ en los cuatro subrectángulos $$R_{11}=[0,1]\times [0,1] \ ,\ \ R_{12}=[0,1]\times [1,2] \ ,\ \ R_{21}=[1,2]\times [0,1] \ ,\ \ R_{22}=[1,2]\times [1,2]$$ y dibujamos sobre $S$ (que es la parte de $z=9-x^2-y^2$ que se proyecta sobre $R$) los correspondientes cuatro parches. En cada uno de estos parches tomamos el punto $P_{ij}$ correspondiente a las coordenadas $x$ e $y$ máximas. Se halló el vector normal en los puntos $P_{ij}$, y se evaluaron los cuatro productos $|{\bf N}|\mbox{área}(R_{ij})$

Supón ahora que $g(x,y,z)=x^2+z^2$ diera en cada punto el valor de la densidad de masa superficial. Calcula una aproximación de la masa de $S$ sumando los cuatro valores $$g(P_{ij})|{\bf N}|\mbox{área}(R_{ij})$$

Solución
Los valores de $g$ que hemos de tomar son $$g(P_{11})=50\ \ ,\ \ g(P_{12})=17\ \ ,\ \ g(P_{21})=20\ \ ,\ \ g(P_{22})=5$$ luego la suma pedida es $$50\cdot 3+37\sqrt{21}+5\sqrt{33}\approx 348.278$$ La masa que se obtiene realizando la integral con Matlab resulta 494.361: $$\mbox{masa}=\int_0^2\!\! \int_0^2 (x^2+(9-x^2-y^2)^2)\sqrt{4(x^2+y^2)+1}\, dx\, dy\approx 494.361$$

Ejercicio 9

Si $x$, $y$ y $z=f(x,y)$ son longitudes medidas en cm. y $g(x,y,z)$ es la densidad de masa superficial de una lámina $S$ en gr$/\mbox{cm}^2$, indica en qué se mide
  1. $f'_x(x,y)$
  2. $\sqrt{f'_x(x,y)^2+f'_y(x,y)^2+1}$
  3. $dS=\sqrt{f'_x(x,y)^2+f'_y(x,y)^2+1}\, dx \, dy$
  4. $g(x,y,f(x,y))\, dS$
  5. $M=\int\!\!\int_S g(x,y,f(x,y))\, dS$
  6. $\frac{M}{\mbox{área(S)}}$
Pista
Solución
Recuerda que la derivada es el límite de un cociente incremental. Por ejemplo, si $x=g(t)$ es longitud y $t$ es tiempo, la derivada de $x=g(t)$ respecto de $t$ es el límite del cociente entre un incremento de $x$ (por tanto una longitud) y un incremento de $t$ (por tanto un tiempo); así, esa derivada será una velocidad.
  1. $f'_x(x,y)$ es adimensional
  2. $\sqrt{f'_x(x,y)^2+f'_y(x,y)^2+1}$ es adimensional
  3. $dS=\sqrt{f'_x(x,y)^2+f'_y(x,y)^2+1}\, dx \, dy$ se mide en $\mbox{cm}^2$ pues es un área
  4. $g(x,y,f(x,y))\, dS$ se mide en gramos, pues es una masa
  5. $M=\int\!\!\int_S g(x,y,f(x,y))\, dS$ se mide en gramos, pues es una masa
  6. $\frac{M}{\mbox{área(S)}}$ se mide en gr$/\mbox{cm}^2$, pues es una densidad de masa superficial

Ejercicio 10

Encuentra ${\bf F}\cdot{\bf N}(x,y,f(x,y))$ para $z=f(x,y)=x+y^2$ siendo
  1. ${\bf F}(x,y,z)=(xz,z-x,y^2)$
  2. ${\bf F}(x,y,z)=zx^2\,{\bf i}-y^2\,{\bf j}+z\,{\bf k}$
Pista
Solución
Recuerda que un vector normal en cada punto de la superficie $z=f(x,y)$ es ${\bf N}=(-f'_x,-f'_y,1)$
el vector normal en cada punto es ${\bf N}=(-1,-2y,1)$
  1. ${\bf F}\cdot{\bf N}(x,y,z)=-xz-2y(z-x)+y^2$ luego $${\bf F}\cdot{\bf N}(x,y,f(x,y))=-x(x+y^2)-2y^3+y^2$$
  2. ${\bf F}\cdot{\bf N}(x,y,z)=-zx^2+2y^3+z$ luego $${\bf F}\cdot{\bf N}(x,y,f(x,y))=(x+y^2)(1-x^2)+2y^3$$

Ejercicio 11

Si $x$, $y$ y $z=f(x,y)$ son longitudes medidas en m. y ${\bf V}$ es un campo de velocidades (en $\mbox{m}/\mbox{sg}$) en el que está inmerso una lámina $S$, indica en qué se mide
  1. ${\bf V}\cdot{\bf N}$
  2. ${\bf V}\cdot{\bf N}\, dA$
  3. $I=\int\!\!\int_S {\bf V}\cdot{\bf N}\, dA$
  4. $\frac{I}{\mbox{área(S)}}$
Pista
Solución
Ten en cuenta que cada componente del vector normal es adimensional, pues es la derivada de una longitud respecto de una longitud.
  1. ${\bf V}\cdot{\bf N}$ se mide en m/sg
  2. ${\bf V}\cdot{\bf N}\, dA$ se mide en m$^3$/sg, observa que es un flujo
  3. $I=\int\!\!\int_S {\bf V}\cdot{\bf N}\, dA$ se mide en m$^3$/sg, observa que es un flujo
  4. $\frac{I}{\mbox{área(S)}}$ se mide en m/sg, pues es la velocidad media

Ejercicio 12

Analiza si las siguientes superficies son cerradas
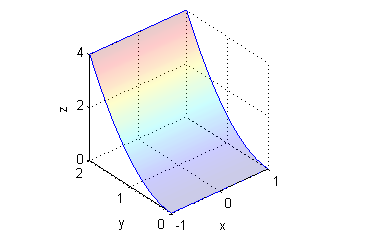
  1. $z=y^2$ para $(x,y)\in R_{xy}=[-1,1]\times[0,2]$;
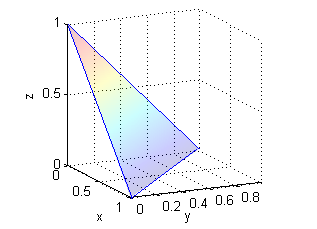
  2. parte de $x+y+z=1$ en el primer octante;
  3. $x^2+y^2+(z-1)^2=4$;
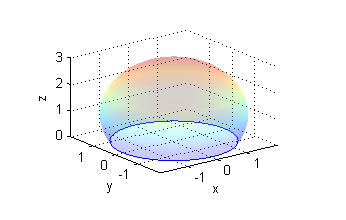
  4. parte de $x^2+y^2+(z-1)^2=4$ en $z>0$.
Solución
  1. es una porción de cilindro parabólico, no es cerrada:
    Gráfica
  2. es una porción de plano, no es cerrada
    Gráfica
  3. es una esfera completa, por tanto es cerrada
  4. es una porción de esfera, por tanto no es cerrada:
    Gráfica

Ejercicio 13

Para las superficies no cerradas del ejercicio anterior, que son
  1. $z=y^2$ para $(x,y)\in R_{xy}=[-1,1]\times[0,2]$;
  2. parte de $x+y+z=1$ en el primer octante;
  3. parte de $x^2+y^2+(z-1)^2=4$ en $z>0$.
  1. escribe la expresión de la curva borde (puede ser que sea la unión de varias curvas);
  2. encuentra una o varias superficies con las que ''cerrar'' la superficie, es decir que su unión resulte una superficie cerrada.
Solución apartado a.
  1. la curva borde está formada por cuatro curvas: $$\partial C=\cup_{i=1}^4 C_i$$ siendo
    • $C_1$ el segmento $-1\leq x\leq 1$ en $y=0$ y $z=0$
    • $C_2$ el arco de parábola $z=y^2$ en el plano $x=1$ para $0\leq y\leq 2$
    • $C_3$ el segmento $-1\leq x\leq 1$ en $y=2$ y $z=4$ y
    • $C_4$ el arco de parábola $z=y^2$ en el plano $x=-1$ para $0\leq y\leq 2$
    Gráfica
  2. para ''cerrar'' esta superficie habría que unirle cuatro porciones de planos: las caras verticales en los planos $x=-1$, $x=1$ e $y=2$ y la cara plana en $z=0$

b. Para la parte de $x+y+z=1$ en el primer octante
Solución apartado b.
  1. la curva borde está formada por tres curvas: $$\partial C=\cup_{i=1}^3 C_i$$ siendo
    • $C_1$ el segmento $x+y=1$ en $z=0$ para $x$ e $y$ positivos
    • $C_2$ el segmento $y+z=1$ en $x=0$ para $y$ e $z$ positivos y
    • $C_3$ el segmento $x+z=1$ en $y=0$ para $x$ e $z$ positivos
    Gráfica
  2. para ''cerrar'' esta superficie habría que unirle tres porciones de planos: las tres caras triangulares correspondientes a los planos coordenados

c. Para la parte de $x^2+y^2+(z-1)^2=4$ en $z>0$
Solución apartado c
  1. la curva borde es la circunferencia $x^2+y^2=3$ en el plano $z=0$
    Gráfica
  2. para ''cerrar'' esta superficie habría que unirle el disco $x^2+y^2\leq 3$ en el plano $z=0$

Ejercicio 14

Halla ${\bf rot F}\cdot{\bf N}(x,y,f(x,y))$ para ${\bf F}(x,y,z)=(x+y^2,y-z^2,z+2x)$ y ${\bf N}$ la normal que tiene un 1 en su tercera componente, para cada una de las siguientes superficies
  1. una porción del plano $2x-3y+z=1$;
  2. la parte de $x^2+y^2+z^2=1$ en el primer octante;
  3. una porción de $z=x^2+y^2$.
Pista
Solución apartado a.
Recuerda que si ${\bf F}=M{\bf i}+N \, {\bf j} +P \, {\bf k}$, entonces $${\bf rot F}=\left|\begin{array}{lll} {\bf i} & {\bf j} & {\bf k}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ M & N & P \end{array}\right|$$ y que si una superficie viene dada por $z=f(x,y)$, el vector normal que tiene un 1 en la tercera componente es $${\bf N}=(-f'_x,-f'_y,1)$$
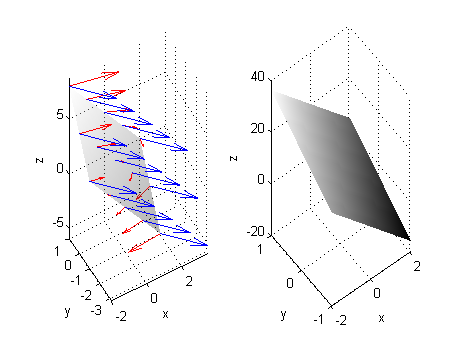
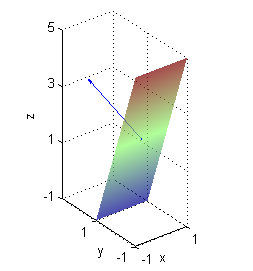
El rotacional es ${\bf rot F}(x,y,z)=2(z,-1,-y)$ y el vector normal es ${\bf N}=(2,-3,1)$, luego ${\bf rot F}\cdot{\bf N}(x,y,z)= 2(2z+3-y)$ por lo que $${\bf rot F}\cdot{\bf N}(x,y,f(x,y))=2(5-4x+5y)$$ Gráfica
A la izquierda puedes ver una porción de la superficie $z=f(x,y)$ con una muestra de vectores normales en azul y una muestra del campo rotacional en rojo. La figura de la derecha es una porción de la superficie $z={\bf rot F}\cdot{\bf N}$. Se he dibujado con el siguiente código: 
  		[X,Y]=meshgrid(-2:.1:2,-1:.1:1);
		    Z=1-2*X+3*Y;
		    AU=ones(size(X));
		    subplot(1,2,1)
		    surf(X,Y,Z,'EdgeColor','none')
		    colormap gray
		    shading interp
		    subplot(1,2,2)
		    surf(X,Y,2*(5-4*X+5*Y))
		    shading interp
		    xlabel('x');ylabel('y');zlabel('z')
		    subplot(1,2,1)
		    hold on
		    [X,Y]=meshgrid(-2:1:2,-1:1:1);
		    AU=ones(size(X)); Z=1-2*X+3*Y;
		    quiver3(X,Y,Z,2*AU,-3*AU,AU);
		    quiver3(X,Y,Z,2*Z,-2*ones(size(X)),-2*Y,'r');%rotacional
		    view([-30,58])
		    alpha(.3)
		axis equal
		xlabel('x');ylabel('y');zlabel('z')
		hold off
b. superficie: parte de $x^2+y^2+z^2=1$ en el primer octante
Solución apartado b.
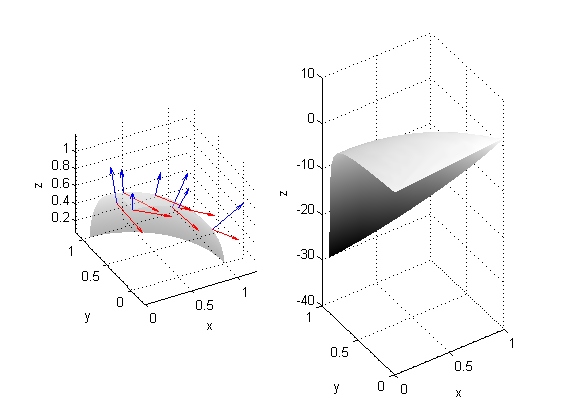
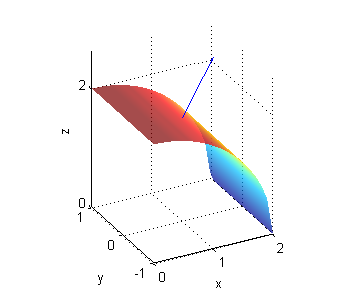
El rotacional es ${\bf rot F}(x,y,z)=2(z,-1,-y)$ y el vector normal es ${\bf N}=(\frac{x}{\sqrt{1-x^2-y^2}},\frac{y}{\sqrt{1-x^2-y^2}},1)$, luego ${\bf rot F}\cdot{\bf N}(x,y,z)= 2(\frac{xz-y}{\sqrt{1-x^2-y^2}}-y)$ por lo que $${\bf rot F}\cdot{\bf N}(x,y,f(x,y))=2(\frac{-y}{\sqrt{1-x^2-y^2}}+x-y)$$ Gráfica
A la izquierda puedes ver una porción de la superficie $z=f(x,y)$ con una muestra de vectores normales en azul y una muestra del campo rotacional en rojo. La figura de la derecha es una porción de la superficie $z={\bf rot F}\cdot{\bf N}$
c. superficie: una porción de $z=x^2+y^2$
Solución
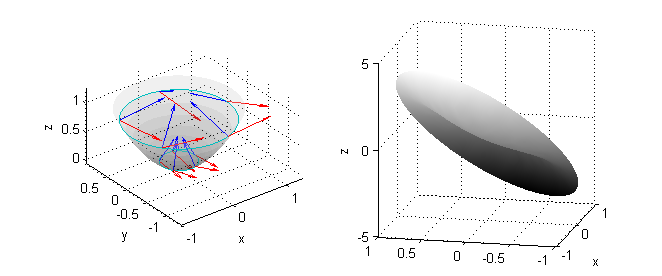
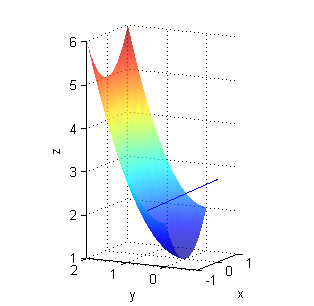
El rotacional es ${\bf rot F}(x,y,z)=2(z,-1,-y)$ y el vector normal es ${\bf N}=(-2x,-2y,1)$, luego ${\bf rot F}\cdot{\bf N}(x,y,z)= 2(-2xz+y)$ por lo que $${\bf rot F}\cdot{\bf N}(x,y,f(x,y))=2(-2x(x^2+y^2)+y)$$ Gráfica
A la izquierda puedes ver una porción de la superficie $z=f(x,y)$ con una muestra de vectores normales en azul y una muestra del campo rotacional en rojo. La figura de la derecha es una porción de la superficie $z={\bf rot F}\cdot{\bf N}$

Ejercicio 15

Sea $C$ la circunferencia $x^2+y^2=1$ en el plano $z=1$. Comprueba que las siguientes superficies cumplen que $\partial S=C$. Represéntalas y orienta $S$ y $C$ con orientaciones conformes (recuerda que orientar una superficie es elegir un sentido para el vector normal):
  1. $S$: disco de centro $(0,0,1)$ y radio 1 en el plano $z=1$;
  2. $S$: porción de $z=2-\sqrt{x^2+y^2}$ para $z\geq 1$;
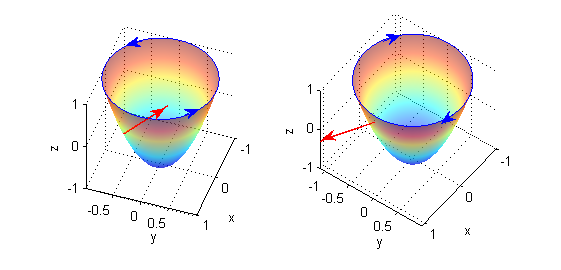
  3. $S$: porción de $z=2(x^2+y^2)-1$ para $z\leq 1$;
  4. $S$: porción de $x^2+y^2+2z^2=3$ para $z\geq 1$.
Pista
Solución
Para que las orientaciones de la superficie y la curva sean conformes debe cumplirse la regla del sacacorchos o bien la regla de que un caminante que siga el sentido de la curva con la cabeza apuntando como indique la normal debe dejar la superficie a mano izquierda.
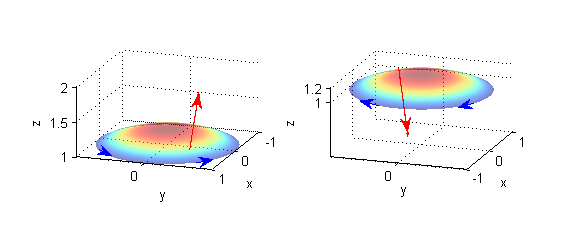
  1. $S$: disco de centro $(0,0,1)$ y radio 1 en el plano $z=1$:
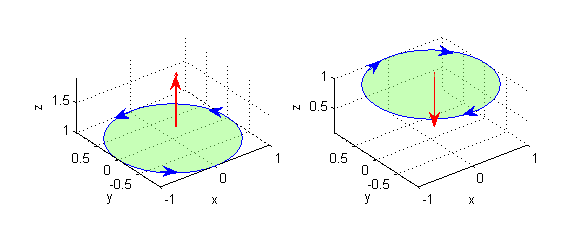
    Gráfica
  2. $S$: porción de $z=2-\sqrt{x^2+y^2}$ para $z\geq 1$:
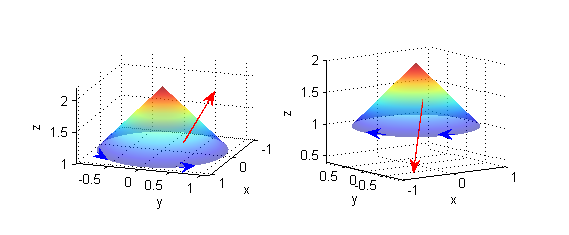
    Gráfica
  3. $S$: porción de $z=2(x^2+y^2)-1$ para $z\leq 1$:
    Gráfica
  4. $S$: porción de $x^2+y^2+2z^2=3$ para $z\geq 1$:
    Gráfica