TEOREMA

Hipótesis: los elementos que intervienen en este teorema son

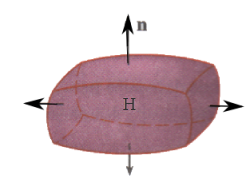
$\;\;\;\;\;\; \bullet$ la superficie suave por partes $S$ que es cerrada, orientada según la normal unitaria exterior, ${\bf n}$;
$\;\;\;\;\;\; \bullet$ la región $H$ del espacio limitada por la superficie $S$; se escribe $\partial H=S$;
$\;\;\;\;\;\; \bullet$ un campo vectorial ${\bf F}(x,y,z)$ de clase $C^1$ sobre $H$ y $\partial H$;

Tesis: bajo estas hipótesis se verifica que $$\int \int_{\partial H}{\bf F}\cdot{\bf n}\, dS=\int \int \int_H \mbox{div}\,{\bf F}\, dV$$