Si la superficie $S$ está sumergida en un fluido que tiene un campo de velocidades continuo ${\bf F}$ y si $\Delta S$ es el área de una pequeña parte de $S$, sobre la cual ${\bf F}$ se puede suponer constante, podemos escribir $$\Delta V \approx {\bf F}\cdot {\bf n}\, \Delta S$$ donde $\Delta V$ es el volumen de fluido que cruza ese pedazo de área en dirección y sentido de un vector normal unitario ${\bf n}$.

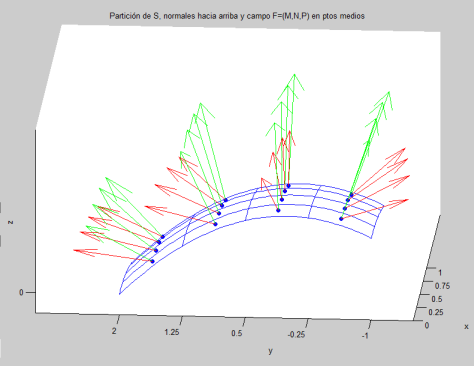
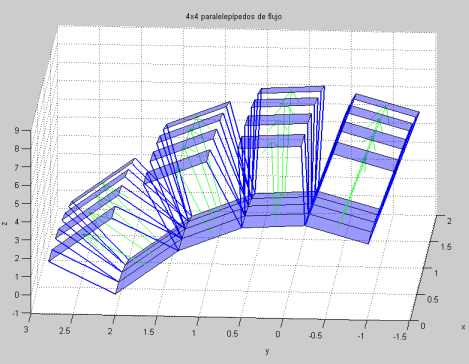
Reuniendo todos esos pequeños volúmenes obtendremos que el flujo total de ${\bf F}$ a través de $S$ es la integral $$\mbox{Flujo}=\int \int_S {\bf F}\cdot{\bf n} \, dS$$

Esta misma expresión es válida para cualquier otro tipo de flujo, como puede ser el eléctrico, el de calor, etc.