Índice de tema

 

Enunciado

Este ejercicio trata sobre el cálculo de las sumas de Riemann en el supuesto de que no se conozca la expresión de la función de dos variables cuyas sumas deben evaluarse, sino únicamente una muestra de valores sobre una malla de puntos de un rectángulo. En el ejercicio anterior se supuso que los puntos estaban igualmente espaciados en amabos ejes; en este ejercicio se trabaja con el supuesto de que esto no sea así.
  • CASO 1: Los puntos de la malla están igualmente espaciados en cada eje: ver ejercicio anterior.
  • CASO 2: Los puntos de la malla no están igualmente espaciados en uno o en los dos ejes; por ejemplo, el conjunto de puntos de la malla tiene de abscisas $[0,\, .2,\, .43,\, .6,\, .84,\, 1]$ y de ordenadas $[1,\, 1.25,\, 1.5,\, 1.84,\, 2.2,\, 2.4,\, 2.78,\, 3.1]$. Igual que en el caso anterior, lo que conocemos de la función son los puntos sobre la malla formada por estas abscisas y estas ordenadas:
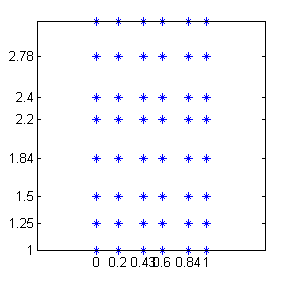
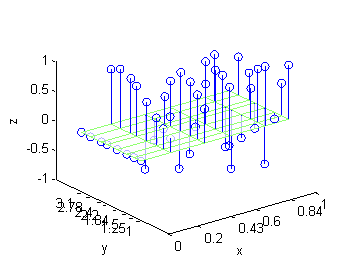
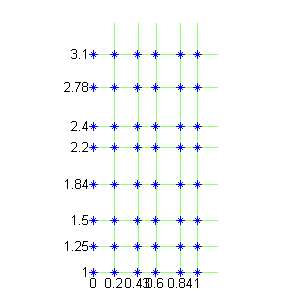
    GráficaGráfica
    • Escribe dos funciones, llamadas sumasRdatos2 y sumasRdatos2b, que tengan como variable de entrada el vector de abscisas, el vector de ordenadas de los puntos de la malla y la matriz de datos y cuya salida sea la suma de Riemann correspondiente a los dos supuestos siguientes:
      • como en el apartado anterior, los puntos de la malla son los vértices inferiores izquierdos de una partición de subrectángulos; el rectángulo total lo obtendremos considerendo que los puntos más a la derecha y los puntos más altos corresponden a subrectangulos de dimensiones medias:
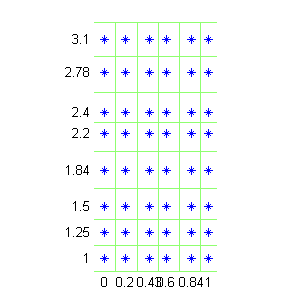
        Gráfica
      • los puntos de la malla no están en los lados ni en los vértices de los subrectángulos de la partición, sino que son interiores a esos subrectángulos:
        Gráfica
    • Prueba las funciones sumasRdatos2 y sumasRdatos2b con los puntos indicados antes y la matriz de datos que se generaría evaluando la función $f(x,y)=\mbox{sen}(xy^2+x^2)$ sobre esta red de puntos, tanto en la primera opción como en la segunda.
    • Analiza cómo están de cerca esos valores entre sí y al valor obtenido utilizando el paquete simbólico.

Resolución del primer apartado del CASO 2

Primer supuesto

En este primer supuesto los puntos de la malla son los extremos izquierdos de los subrectángulos de la partición. Por tanto procedemos como en el caso 1. La diferencia con el caso 1 es que ahora las distancias en horizontal y vertical entre los puntos hay que calcularlas todas, no basta medir el incremento entre las dos primeras como hicimos antes. Para generar un vector con los incrementos en el eje x, que se llamará dx, escribimos 
n=length(x);
dx=abs(x(2:n)-x(1:n-1)); % en cada componente k se guarda la distancia horizontal entre x(k+1) y x(k)
dx(n)=mean(dx); % dimensión horizontal del último subrectángulo
Escribe tú las correspondientes al eje vertical y pulsa en 'Ver'.
Ver
Pondremos 
m=length(y);
dy=abs(y(2:m)-y(1:m-1)); % en cada componente k se guarda la distancia vertical entre y(k+1) e y(k)
dy(m)=mean(dy);  % dimensión vertical del último subrectángulo
Ahora podemos generar una malla con esas dimensiones, 
[DX DY]=meshgrid(dx,dy); %malla de dimensiones
y calcular la correspondiente suma de Riemann: 
V=DX.*DY.*D; % producto de las dimensiones por el valor de la función
s=sum(V(:)) % suma de Riemann
Estas órdenes las escribiremos formando una función, añadiendo las líneas de comentario explicativas de lo que hace la función: 
function s=sumasRdatos2(x,y,D)
%%% ...líneas de comentario explicativas
n=length(x);
dx=abs(x(2:n)-x(1:n-1));    % en cada componente k se guarda la distancia horizontal entre x(k+1) y x(k)
dx(n)=mean(dx);             % dimensión horizontal del último subrectángulo
m=length(y);
dy=abs(y(2:m)-y(1:m-1));    % en cada componente k se guarda la distancia vertical entre y(k+1) e y(k)
dy(m)=mean(dy);  			% dimensión vertical del último subrectángulo
[DX DY]=meshgrid(dx,dy); 	% malla de dimensiones
V=DX.*DY.*D; 				% producto de las dimensiones por el valor de la función
s=sum(V(:)) 				% suma de Riemann
end

Continuación de la Resolución del primer apartado del CASO 2

Segundo supuesto

Consideramos ahora que los puntos de la malla no estén en las aristas ni los vértices de los subrectángulos de la partición, sino que sean puntos interiores a estos subrectángulos. La parte de la función sumasRdatos2 donde se calculan los vectores dx y dy no cambiaría; sí es diferente la matriz de dimensiones; hemos de generarla de forma que la arista de cada subrectángulo equidiste en horizontal y vertical de los de los puntos correspondientes a los subrectángulos que lo rodean. Si en el vector dimx guardamos las dimensiones en horizontal de los subrectángulos de la partición, podemos poner 
n=length(x);
dimx(2:n-1)=(dx(1:n-2)+dx(2:n-1))/2; % longitud de cada subrectángulo intermedio
dimx(1)=dx(1); % longitud del primer subrectángulo
dimx(n)=dx(n-1); % longitud del último subrectángulo
Escribe tú las correspondientes al eje vertical y pulsa en 'Ver'.
Ver
Pondremos 
m=length(y);
dimy(2:m-1)=(dy(1:m-2)+dy(2:m-1))/2; % altura de cada subrectángulo intermedio
dimy(1)=dy(1); % altura del primer subrectángulo
dimy(m)=dy(m-1); % altura del último subrectángulo
Ahora generaremos una malla con esas dimensiones y el resto de la función queda igual que en la otra opción. Así que tendríamos 
function sb=sumasRdatos2b(x,y,D)
%%% ...líneas de comentario explicativas
n=length(x);
dx=abs(x(2:n)-x(1:n-1));    % en cada componente k se guarda la distancia horizontal entre x(k+1) y x(k)
m=length(y);
dy=abs(y(2:m)-y(1:m-1));    % en cada componente k se guarda la distancia vertical entre y(k+1) e y(k)
dimx(2:n-1)=(dx(1:n-2)+dx(2:n-1))/2; % longitud de cada subrectángulo intermedio
dimx(1)=dx(1); % longitud del primer subrectángulo
dimx(n)=dx(n-1); % longitud del último subrectángulo
dimy(2:m-1)=(dy(1:m-2)+dy(2:m-1))/2; % altura de cada subrectángulo intermedio
dimy(1)=dy(1); % altura del primer subrectángulo
dimy(m)=dy(m-1); % altura del último subrectángulo
[DX DY]=meshgrid(dimx,dimy); 	% malla de dimensiones
V=DX.*DY.*D; 				% producto de las dimensiones por el valor de la función
sb=sum(V(:)) 				% suma de Riemann
end

Resolución del segundo apartado del CASO 2

Para probar sumasRdatos2(x,y,D) y sumasRdatos2b(x,y,D) pondremos 
x=[0, .2 , .43 , .6,  .84 , 1];
y=[1,  1.25,  1.5,  1.84,  2.2,  2.4,  2.78,  3.1];
[X,Y]=meshgrid(x,y);
D=sin(X.*Y.^2+X.^2);
s=sumasRdatos2(x,y,D);
sb=sumasRdatos2b(x,y,D);
de cuya ejecución obtendremos 
s= 0.7194
y 
sb=0.6989

Resolución del tercer apartado del CASO 2

Debemos ahora utilizar el paquete simbólico para hallar los valores de la integral de $f(x,y)=\mbox{sen}(xy^2+x^2)$ sobre los rectángulos correspondientes a cada supuesto. Para el primer supuesto, el rectángulo es $R=[0,1.2]\times[1,3.4]$ y para el segundo es $R=[-.1,1.08]\times[.875,3.26]$, así que hallaremos las integrales escribiendo 
syms xs ys
int1=double(int(int(sin(xs*ys^2+xs^2),xs,0,1.2),ys,1,3.4))
int2=double(int(int(sin(xs*ys^2+xs^2),xs,-.1,1.08),ys,.875,3.26))
Nos devolverá 
int1=0.6606
e 
int2=0.7076