Enunciado
Una placa tiene la forma y dimensiones que ves en la figura.
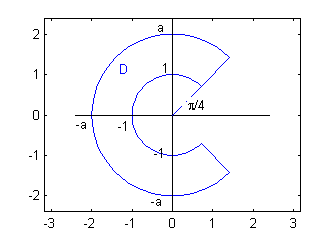
Colocada en los ejes como está en la figura, el valor de la densidad superficial en cada punto $(x,y)$ es la suma de las distancias de $(x,y)$ a los ejes OX y OY.
- Encuentra el valor del radio mayor, $a$, para que la masa de la placa sea $M=14$.
- En el supuesto del apartado anterior, halla los puntos de la placa cuya densidad sea media.
- Dibuja con el ordenador la placa coloreada según la densidad y los puntos donde se alcanza el valor medio de la densidad.
- Analiza si hay otros valores de los radios menor y mayor de la placa para que la masa sea $M=14$ y el valor promedio sea el mismo que obtuviste en el segundo apartado. Deberás utilizar el ordenador para averiguarlo.
Resolución del primer apartado
Paso 1
Saber qué integral debe hacerse. El cálculo de la masa de una placa es una de las interpretaciones de la integral doble más sencillas. Si $d(x,y)$ es la función de densidad de la placa $D$, su masa es: $$\mbox{Masa}(D)=\int\!\!\int_D d(x,y) \, dA$$ Además la función densidad es en este caso $\ldots$
$$d(x,y)=\sqrt{x^2+y^2}$$
$$d(x,y)=x+y$$
$$d(x,y)=|x|+|y|$$
No es correcto; esa sería la distancia al origen
No es correcto; eso no son distancias
En efecto, esa es la expresión de la densidad. Observamos que tanto la placa como la función de densidad que debemos integrar sobre ella son simétricas respecto del eje horizontal, es decir, la masa de la media placa correspondiente a $y$ positivo es la misma que la masa de la media placa inferior, luego
$$\mbox{Masa}(D)=2\mbox{Masa}(D_s)=2\int\!\!\int_{D_s} d(x,y) \, dA$$
siendo $D_s$ la media placa superior.
Paso 2
Preparar el dominio de integración para poder calcular la integral doble. Dado que este dominio es una sección de corona circular, parece indicado el uso de coordenadas polares $(r,\theta)$. Escribe el conjunto $D_s$ mediante esas coordenadas y pulsa en 'Ver'
Ver
$$D_s=\{(r,\theta)\ / \frac{\pi}{4}\leq \theta \leq \pi,\ 1\leq r\leq a\}$$
Paso 3
Plantemos las iteradas y las calculamos. $$\mbox{Masa}(D)=2\int\!\!\int_{D_s} d(x,y) \, dA=2\int_{\pi/4}^{\pi}\int_1^a r^2(|\cos \theta|+|\mbox{sen}\, \theta|) \, dr\, d\theta$$ Una vez que hallemos la integral en $r$, resulta $$\mbox{Masa}(D)=\frac{2}{3}(a^3-1)\int_{\pi/4}^{\pi} (|\cos \theta|+|\mbox{sen}\, \theta|) \, d\theta$$ Ahora debemos calcular la integral en $\theta$. Hazla y elige la opción correcta:
$$\int_{\pi/4}^{\pi} (|\cos \theta|+|\mbox{sen}\, \theta|) \, d\theta=1$$
Ninguna de las opciones propuestas es correcta.
$$\int_{\pi/4}^{\pi} (|\cos \theta|+|\mbox{sen}\, \theta|) \, d\theta=1-\frac{\sqrt{2}}{2}$$
$$\int_{\pi/4}^{\pi} (|\cos \theta|+|\mbox{sen}\, \theta|) \, d\theta=3$$
No es correcto; ¿has tenido en cuenta los valores absolutos?
Hay una correcta.
No es correcto; ¿has tenido en cuenta los signos del coseno y del seno?
En efecto,
- teniendo en cuenta que el coseno es positivo hasta $\frac{\pi}{2}$ y negativo entre $\frac{\pi}{2}$ y $\pi$, $$\int_{\pi/4}^{\pi} |\cos \theta| \, d\theta=\int_{\pi/4}^{\pi/2} \cos \theta \, d\theta-\int_{\pi/2}^{\pi} \cos \theta \, d\theta=$$ $$=\mbox{sen}\,\theta]_{\pi/4}^{\pi/2}-\mbox{sen}\,\theta]_{\pi/2}^{\pi}= 1-\frac{\sqrt{2}}{2}+1=2-\frac{\sqrt{2}}{2}$$
- por otra parte, el seno es positivo entre $\frac{\pi}{4}$ y $\pi$, luego $$\int_{\pi/4}^{\pi} |\mbox{sen}\, \theta| \, d\theta=\int_{\pi/4}^{\pi} \mbox{sen}\, \theta \, d\theta=-\cos \theta ]_{\pi/4}^{\pi}=1+\frac{\sqrt{2}}{2}$$
Paso 4
Finalmente obtenemos el valor de $a$ igualando la masa a 14: $$\mbox{Masa}(D)=2(a^3-1)=14 \ \ \Rightarrow \ \ a=2$$Resolución del segundo apartado
Paso 1
Hallar el valor medio de la densidad. Por lo que sabemos de las interpretaciones de la integral doble, su fórmula es: $$\mbox{densidad media}=d_m=\frac{\mbox{Masa(D)}}{\mbox{Área(D)}}$$ Puesto que la masa ya está calculada, sólo falta hallar el área de $D$. Hazlo para el caso en que el radio mayor sea $a$ y después ya sustituyes $a=2$. Pulsa en 'Ver' cuando lo tengas.
Ver
Puesto que la placa $D$ es simétrica respecto del eje horizontal,
$$\mbox{Área}(D)=\int\!\!\int_D dA=2\int_{\pi/4}^\pi \int_1^a r\,dr\,d\theta=\frac{3\pi}{4}(a^2-1)$$
Para el valor del radio $a=2$, el área es
$$\mbox{Área}(D)=\frac{9\pi}{4}$$
El valor medio resulta
$$d_m=14\frac{4}{9\pi}=\frac{56}{9\pi}$$
Paso 2
Localizar los puntos de la placa donde se alcanza ese valor. Inténtalo y pulsa en 'Ver'.
Ver
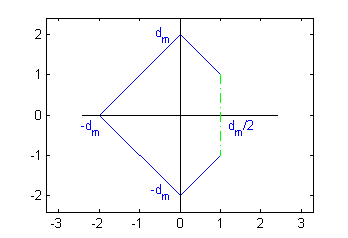
Puesto que la función densidad en cada punto $(x,y)$ es $d(x,y)=|x|+|y|$, la densidad vale $d_m$ en los puntos que cumplan
$$|x|+|y|=d_m$$
Estos son los puntos de la placa que además estén en los lados del cuadrado que tiene sus vértices en los ejes, equidistando $d_m$ del origen de coordenadas; son los puntos en azul de la siguiente figura:

Resolución del tercer apartado
Paso 1
Dibujar la placa coloreada según la función densidad. Para ello, dibujaremos la superficie $z=d(x,y)$ y la veremos desde arriba.- Generamos los vectores de coordenadas $r$ y $\theta$ necesarios para dibujar la superficie:
r=1:.1:2; t=pi/4:pi/32:7*pi/4;
- Generamos una malla y dibujamos la superficie:
[R,T]=meshgrid(r,t); Z=abs(R)+abs(T); surf(R,T,Z)
x=r.*cos(t); y=r.*sin(t); [X,Y]=meshgrid(x,y); Z=abs(X)+abs(Y); surf(X,Y,Z)
[R,T]=meshgrid(r,t); X=R.*cos(T); Y=R.*sin(T); Z=abs(X)+abs(Y); surf(X,Y,Z)
Eso no tiene sentido; eso no dibuja la placa y además la densidad no viene dada por esa función.
Te daría error, pues los vectores r y t no tienen la misma dimensión. Lo que has de hacer es una malla en las variables r y t, para luego pasarla a cartesianas.
Esta opción es correcta.
- Quedará más realista si ponemos la misma escala en los ejes
axis equal
- Nos falta verla desde arriba y darle un aspecto más continuo quitándole el enrejado:
shading interp % quita el enrejado view([0,90]) % la enseña desde 'arriba'
Todo seguido resulta
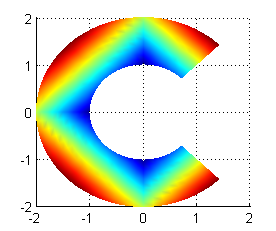
r=1:.1:2; t=pi/4:pi/32:7*pi/4; [R,T]=meshgrid(r,t); X=R.*cos(T); Y=R.*sin(T); Z=abs(X)+abs(Y); surf(X,Y,Z) shading interp view([0,90])y nos dibuja

Paso 2
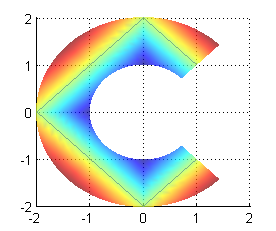
Debemos añadir a la figura los puntos que tienen densidad media $d_m=\frac{56}{9\pi}$. Para ello utilizaremos el comando plot para que dibuje los segmentos rectos que obtuvimos en el apartado anterior. Es necesario saber que las coordenadas de los cinco puntos que deben unirse son, $$(\frac{d_m}{2},\frac{d_m}{2}) \ , \ (0,d_m) \ , \ (-d_m,0) \ , \ (0,-d_m) \ , \ (-\frac{d_m}{2},-\frac{d_m}{2})$$ Escribe el comando plot con estos puntos y pulsa en 'Ver'
Ver
dm=56/(9*pi); % para facilitar la escritura plot([dm/2 0 -dm 0 dm/2],[dm/2 dm 0 -dm -dm/2]) % el primer vector son las abscisas y el segundo las ordenadasSi queremos verlo superpuesto a la placa, añadiremos a las líneas que la dibujaban lo siguiente:
alpha(.8) hold on dm=56/(9*pi); % para facilitar la escritura plot([dm/2 0 -dm 0 dm/2],[dm/2 dm 0 -dm -dm/2]) % el primer vector son las abscisas y el segundo las ordenadas hold offy en la figura tendremos:
Resolución del cuarto apartado
Suponemos ahora que el radio mayor, $a$ vuelve a estar indeterminado y que lo mismo ocurre con el radio menor, que llamaremos $b$. Hemos de averiguar cuánto pueden valer para que la masa y la densidad media sean $$M=14 \hspace{.5cm} \mbox{y} \hspace{.5cm} d_m=\frac{56}{9\pi}$$ y por tanto el área resulte $$\mbox{Área}(D)=\frac{9\pi}{4}$$ Siguiendo los pasos del primer apartado, la masa en función de $a$ y $b$ resulta $$\mbox{Masa}(D)=2(a^3-b^3)$$ y siguiendo el cálculo del área que se hizo en el segundo apartado, tenemos $$\mbox{Área}(D)=\frac{3\pi}{4}(a^2-b^2)$$ luego $$a^3-b^3=7 \hspace{.5cm} \mbox{y} \hspace{.5cm} a^2-b^2=3$$ Intenta escribir a partir de estas dos ecuaciones, una para la incógnita $b$. Pulsa en 'Ver' cuando lo tengas.
Ver
Hay varias alternativas para conseguir esto. Una sencilla es multiplicar por $a$ la segunda y restarla de la primera. Otra opción es escribir
$$a=\frac{a^3}{a^2}=\frac{b^3+7}{b^2+3} \hspace{.5cm} \Rightarrow \hspace{.5cm} a^2=\left(\frac{b^3+7}{b^2+3}\right)^2=b^2+3\hspace{.5cm} \Rightarrow \hspace{.5cm} (b^3+7)^2=(b^2+3)^3$$
Desarrollando esas potencias y operando,
$$b^6+14b^3+49=b^6+9b^4+27b^2+27\hspace{.5cm} \Rightarrow \hspace{.5cm} 9b^4-14b^3+27b^2-22=0$$
Piensa cómo pedirle al ordenador las raíces de ese polinomio y pulsa en 'Continuar'.
Una opción es definir el polinomio mediante sus coeficientes, poniendo
p=[9 -14 27 0 -22];para después pedirle sus raíces con
roots(p)Si ejecutas estas dos órdenes, sabrás que las raíces son
0.6402 + 1.7212i 0.6402 - 1.7212i 1.0000 -0.7248es decir, la única real positiva es $b=1$, que como sabemos ocasiona que $a=2$. Se concluye por tanto que esta es la única opción para los radios manteniendo la masa y la media de la densidad dadas.