Enunciado
Dada la función $f(x,y)=xy$ y la región plana
$$D=\{(x,y)/\, 0\leq y\leq 1,\, 0\leq x\leq 2y^2\}$$
- Encuentra el valor de la integral de $f(x,y)$ sobre $D$ utilizando el orden de integración en el que viene dado $D$. Comprueba el resultado en el ordenador.
- Dibuja la región $D$ primero a mano y luego con el ordenador.
- Halla el valor de esa misma integral, pero con el otro orden de integración.
- Calcula el valor promedio de $f(x,y)$ en $D$.
Resolución del primer apartado
Paso 1
Saber qué integral debe hacerse. Teniendo en cuenta la construcción de las integrales iteradas, debemos escribir:
$$I=\int_0^1{\int_0^{2y^2}{xy}\, dy}\, dx$$
$$I=\int_0^{2y^2}{\int_0^1{\, xy}\, dy}\, dx$$
$$I=\int_0^1{\int_0^{2y^2}{xy} \, dx}\, dy$$
¡No! El orden de los diferenciales no es correcto.
¡No! ¡Nunca la intregral más exterior puede tener extremos en las variables de integración!
Es correcto. Esa es la integral escrita como dos iteradas.
Paso 2
Hacer la integral más interior: $$\int_0^{2y^2}{xy}\, dx$$ dejando la variable $y$ como parámetro. Así $$\int_0^{2y^2}{xy}\, dx=\left.\frac{1}{2}x^2y\right]_0^{2y^2}=\frac{1}{2}4y^4y=\underbrace{2y^5}_{\text{Sólo función de }y}$$Paso 3
La segunda integral será entonces: $$I=\int_0^1{2y^5}dy$$ resolviendo $$I=\left.2\, \frac{1}{6} \, y^6\right]_0^1=\underbrace{\frac{1}{3}}_{\text{Constante}}$$Paso 4
Para comprobar en el ordenador si este resultado es correcto, podemos hacersyms x y int(int(x*y,x,0,2*y^2),y,0,1)
Resolución del segundo apartado
Paso 1
La dibujamos a mano. De las siguientes regiones planas
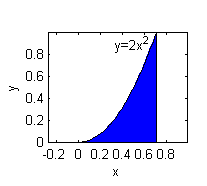
La de la izquierda (azul)
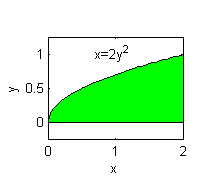
La del medio (verde)
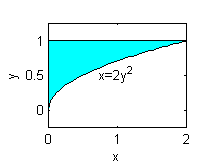
La de la derecha (azul turquesa)
¡No! la curva que limita la región no es la adecuada.
No. La región de la figura sería $$\{(x,y)/\, 0\leq y\leq 1,\, 2y^2\leq x\leq 1\}$$
En efecto, esa es la correcta.
Paso 2
La dibujamos en el ordenador. Para dibujar este tipo de regiones, podemos recurrir al comando fill, que rellena el contorno determinado por los puntos cuyas abscisas y ordenadas estén en su primer y segundo argumento, respectivamente. El tercer argumento, obligatorio, es el color de relleno:
y=linspace(0,1,50); % tomamos 50 valores entre 0 y 1
fill([0 2*y.^2],[1 y],'c'); % el primer pto del contorno es (0,1) y después los de la curva x=2y^2
axis equal
xlabel('x');ylabel('y')
Resolución del tercer apartado
Paso 1
Escribimos la región $D$ para integrar sobre ella en el otro orden de integración. Debemos poner
$$D=\{(x,y)/\, 0\leq x\leq 2,\, 0\leq y\leq \sqrt{x/2}\}$$
Ninguna de las dos opciones es correcta.
$$D=\{(x,y)/\, 0\leq x\leq 2,\, \sqrt{x/2}\leq y\leq 1\}$$
No, la región así descrita sería
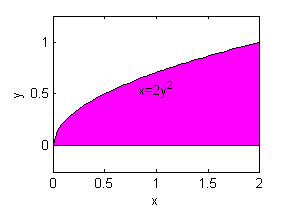

Míralo bien, sí hay una correcta.
Esta opción es correcta.
Paso 2
Plantea la integral con este orden de integración y halla su valor calculando las integrales iteradas. Pulsa en 'Ver' cuando lo tengas.
Ver
La integral es
$$I=\int_0^2\int_{\sqrt{x/2}}^1 xy\, dy\, dx$$
Calculamos las iteradas:
$$I=\int_0^2\int_{\sqrt{x/2}}^1 xy\, dy\, dx=\int_0^2 \left. x\frac{y^2}{2}\right]_{\sqrt{x/2}}^1\, dx=
\int_0^2 \frac{x}{2}(1-\frac{x}{2})\, dx=$$ $$=\frac{1}{4}\int_0^2(2x-x^2)\, dx=\frac{1}{4}(x^2-\frac{1}{3}x^3)]_0^2=\frac{1}{3}$$
Resolución del cuarto apartado
El valor promedio de una función $f(x,y)$ sobre una región $D$ es $$f_m=\frac{\int\!\!\int_D f(x,y)\, dA}{\mbox{área}(D)}=\frac{\int\!\!\int_D f(x,y)\, dA}{\int\!\!\int_D dA}$$ Calcula el valor promedio para la función y la región de este ejercicio. Pulsa en 'Ver' cuando lo tengas.
Ver
El área de la región es
$$\mbox{área}(D)=\int\!\!\int_D dA=\int_0^1 \int_0^{2y^2} dx\, dy=2\int_0^1 y^2\, dy=\frac{2}{3}$$
con lo que el valor promedio resulta
$$f_m=\frac{1/3}{2/3}=\frac{1}{2}$$
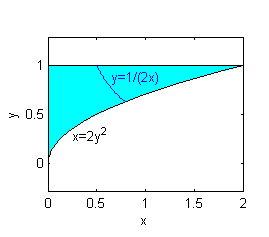
Una cuestión que suele ser de interés es saber cuáles son los puntos de la región en que se alcanza el valor promedio, es decir los que cumplan $f(x,y)=f_m$; en este caso, esta ecuación es $xy=\frac{1}{2}$, lo que significa que los puntos de la región $D$ donde se alcanza ese valor medio son los de la hipérbola $y=1/(2x)$: