Enunciado
Halla el valor de cada integral sin calcular las iteradas:
- $$I=\int_0^2\int_{-\sqrt{2x-x^2}}^{\sqrt{2x-x^2}}dy\, dx$$
- $$J=\int_{-1}^{3}\int_{-1}^{1} x\, dx\, dy$$
- $$K=\int_{-3}^3\int_0^{\sqrt{9-x^2}} \sqrt{9-x^2-y^2} dy\, dx$$
Dibuja en cada caso la región de integración, a mano y en el ordenador.
Resolución del primer apartado
Paso 1
Observamos la función del integrando: concluimos que \(I\) se puede interpretar geométricamente como ... (elige opción) Si no se te ocurre nada, puedes consultar las interpretaciones de la integral doble.
una longitud
un volumen
un área
¡No!
sí, pero volumen dimensionalmente, como número nos sirve para el área
En efecto, esa integral conduce al área de la región de integración.
Paso 2
Analizamos la región de integración. Es ...
$$D=\{(x,y) / \, 0\leq y\leq 2 ,\, -\sqrt{2x-x^2} \leq x \leq \sqrt{2x-x^2}\}$$
Ninguna de las propuestas
$$D=\{(x,y) / \, 0\leq x\leq 2 ,\, -\sqrt{2x-x^2} \leq y \leq \sqrt{2x-x^2}\}$$
¡No! no tiene ningún sentido
Hay una válida
En efecto, esa es la región. Ahora debemos identificarla como un conjunto de puntos conocido, del cual sepamos el área. Piénsalo y pulsa en 'Continuar' cuando lo tengas.
Paso 3
Debemos reconocer qué puntos son los que cumplen que $y^2=2x-x^2$; si completamos cuadrados, escribimos esta ecuación como $(x-1)^2+y^2=1$, que es la ecuación de la circunferencia de centro $(1,0)$ y radio 1. Por tanto, \(D\) es el círculo de centro \((1,0)\) y radio 1. Por tanto, $$I=\pi$$
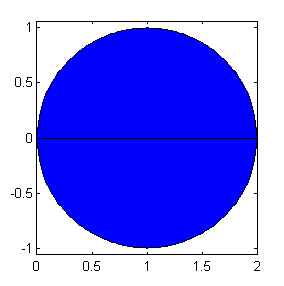
x=0:.02:2; fill([x x],[-sqrt(2*x-x.^2),sqrt(2*x-x.^2)],'b')
Resolución del segundo apartado
$$J=\int_{-1}^{3}\int_{-1}^{1} x\, dx\, dy$$Paso 1
En este caso se integra la función $$f(x,y)=x$$ Analizamos cómo es esta función:
Es par en x
No tiene ningún tipo de simetría
Es impar en x
No, mírala bien
No, mírala bien
En efecto, se trata obviamente de una función con simetría impar en la primera variable
Paso 2
Teniendo en cuenta cómo es el rectángulo de integración, esa simetría se puede aprovechar porque ... (piénsalo y pulsa en 'Ver')
Ver
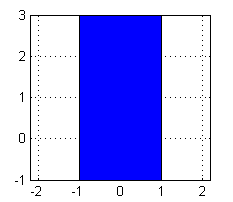
porque el rectángulo de integración, $$R=[-1,1]\times[-1,3]$$
es simétrico en esa misma variable.
Para dibujar este rectángulo, podemos utilizar de nuevo el comando fill ahora dando únicamente los vértices del rectángulo:
fill([-1 1 1 -1],[-1 -1 3 3],'b') axis equal grid on
Sobre el subrectángulo \([-1,0]\times [-1,3]\) la función toma valores opuestos a los que toma sobre
\([0,1]\times [-1,3]\), como gráficamente podemos ver en la siguiente figura
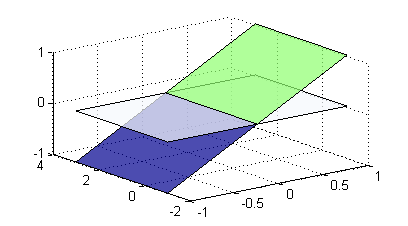
[X,Y]=meshgrid(-1:1,[-1,3]); surf(X,Y,X)Por tanto $$J=0$$
Resolución del tercer apartado
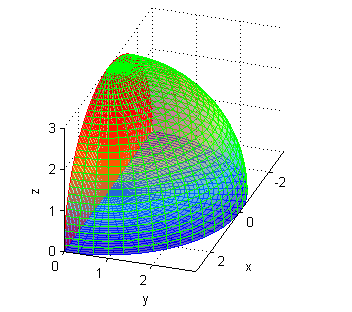
$$K=\int_{-3}^3\int_0^{\sqrt{9-x^2}} \sqrt{9-x^2-y^2} dy\, dx$$Paso 1
¿Qué interpretación geométrica podemos darle a esta integral?
una longitud
un área
un volumen
¡No!
No, no se está integrando la función igual a 1
En efecto, esa integral es el volumen del sólido encerrado entre el plano \(z=0\) y la gráfica de la función \(z=\sqrt{9-x^2-y^2}\) para \(x,y\) variando en ... (escríbelo y pulsa en 'Continuar')
Paso 2
La región de integración es $$D=\{(x,y) / \, -3\leq x\leq 3 ,\, 0\leq y\leq \sqrt{9-x^2}\}$$ Podemos dibujarla en el ordenador escribiendofill(x,sqrt(9-x.^2),'b') axis equal grid on
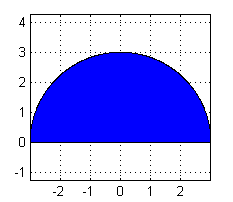
Una esfera de radio 3
Una semiesfera de radio 9
Un cuarto de esfera de radio 9
Ninguna de las propuestas
¡No! Míralo otra vez
¡No! Míralo otra vez
¡No! Míralo otra vez
En efecto, no es ninguna de las propuestas, pues se trata de un cuarto de esfera de radio 3.