Una función $f(x,y)$ es integrable en un conjunto $D \subset R{^2}$ si lo es en un rectángulo que contenga a $D$.

La definición, la interpretación geométrica, las condiciones de existencia y las propiedades de la integral doble sobre rectángulos recogidas en el apartado anterior, son aplicables a la integral doble sobre dominios regulares sin más que sustituir $R$ por $D$.

Existen dos tipos de dominios regulares en $R{^2}$:  x-simple, y-simple.

Definición (Dominio y-simple). Un conjunto $D$ del plano es y-simple si se puede escribir como, $$D = \{ (x,y)/\;a \le x \le b,{\kern 1pt} \,\,\,{\phi _1}(x) \le y \le {\phi _2}(x)\} $$

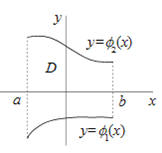
Definición (Dominio x-simple). Un conjunto $D$ del plano es x-simple si se puede escribir como, $$D = \{ (x,y)/\;c \le y \le d,{\kern 1pt} \,\,\,{\psi _1}(y) \le x \le {\psi _2}(y)\} $$                      

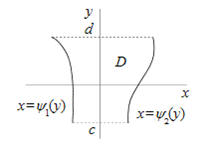
Definición (Integrales iteradas sobre dominios regulares).

$\bullet $ Si conjunto $D$ del plano es y-simple y la función $f$ es integrable en $D$ $$\int \int_D \,f(x,y){\kern 1pt} dA = \int_{\,a}^{\,b} \int_{\,{\phi _1}(x)}^{\,{\phi _2}(x)} f(x,y){\kern 1pt} dy{\kern 1pt} dx$$

$\bullet $ Si conjunto $D$ del plano es x-simple y la función $f$ es integrable en $D$ $$\int \int_D \,f(x,y){\kern 1pt} dA = \int_{\,c}^{\,d} \int_{\,{\psi _1}(y)}^{\,{\psi _2}(y)} f(x,y){\kern 1pt} dx{\kern 1pt} dy$$