Ejercicios preliminares e instantáneos. Integral múltiple (segunda parte)
Ejercicio 1
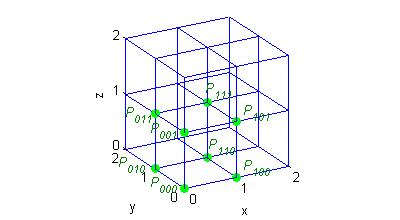
Dibuja la caja $[0,2]\times[0,2]\times[0,2]$ dividida en ocho subcajas iguales. Escribe los ocho puntos correspondientes a las coordenadas $x$, $y$, $z$, mínimas en cada subcaja. Escribe después su fórmula, en función de tres índices.
Pista
Solución
Por ejemplo, $P_{111}(1,1,1)$ es el punto elegido para la caja de vértices $(1,1,1)$, $(1,2,1)$, $(2,1,1)$, $(2,2,1)$, $(1,1,2)$, $(1,2,2)$, $(2,1,2)$, $(2,2,2)$.
Los puntos son $(0,0,0)$, $(0,1,0)$, $(0,0,1)$, $(0,1,1)$, $(1,0,0)$, $(1,1,0)$, $(1,0,1)$ y $(1,1,1)$. Responden a la fórmula $$P_{ijk}=(i,j,k)\ ,\ \ i=0,1\ ,\ \ j=0,1\ ,\ \ k=0,1$$

Ejercicio 2
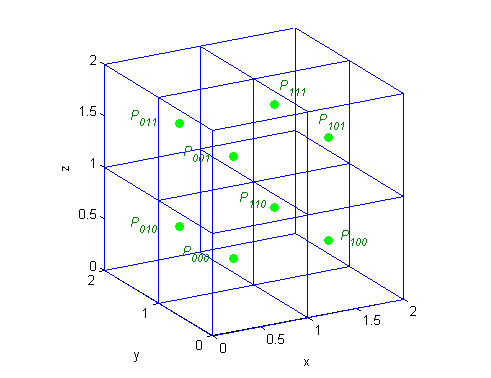
Para la caja $[0,2]\times[0,2]\times[0,2]$ dividida en ocho subcajas iguales, escribe las coordenadas del punto medio de cada una de las ocho subcajas. Escribe después su fórmula, en función de tres índices.
Solución
Los puntos son $\left(\frac{1}{2},\frac{1}{2},\frac{1}{2}\right)$, $\left(\frac{1}{2},\frac{3}{2},\frac{1}{2}\right)$, $\left(\frac{1}{2},\frac{1}{2},\frac{3}{2}\right)$,
$\left(\frac{1}{2},\frac{3}{2},\frac{3}{2}\right)$, $\left(\frac{3}{2},\frac{1}{2},\frac{1}{2}\right)$, $\left(\frac{3}{2},\frac{3}{2},\frac{1}{2}\right)$, $\left(\frac{3}{2},\frac{1}{2},\frac{3}{2}\right)$ y $\left(\frac{3}{2},\frac{3}{2},\frac{3}{2}\right)$. Responden a la fórmula
$$P_{ijk}=\left(\frac{1}{2}+i,\frac{1}{2}+j,\frac{1}{2}+k\right)\ ,\ \ i=0,1\ ,\ \ j=0,1\ ,\ \ k=0,1$$

Ejercicio 3
Para la caja $[0,2]\times[0,2]\times[0,2]$ dividida en ocho subcajas iguales, tomando los puntos medios en las subcajas, escribe la suma de Riemann de la función $f(x,y,z)=x+y-z$. Esta suma da una aproximación de la integral de $f$ sobre la caja.
Pista
Solución
La suma de Riemann es la suma de los valores de la función $f(x,y,z)$ en los puntos elegidos (en este caso los puntos medios) multiplicados cada uno de ellos por el volumen de la subcaja correspondiente; por ejemplo, el primer sumando será el valor de $f(x,y,z)$ en el punto $P_{000}$ multiplicado por el volumen de la subcaja a la que pertenece este punto.
La suma de Riemann pedida es
$$S_8=\sum_{k=0}^1\sum_{j=0}^1\sum_{i=1}^1 f(P_{ijk})=\sum_{k=0}^1\sum_{j=0}^1\sum_{i=1}^1 \left(\frac{1}{2}+i+j-k\right)=\frac{1}{2}+\frac{3}{2}+\frac{3}{2}+\frac{5}{2}-\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{3}{2}=8$$
En este caso, la suma de Riemann es fácil de calcular a mano. También podríamos calcularla en el ordenador, escribiendo
x=1/2+(0:1); % abscisas de los puntos medios [X,Y,Z]=meshgrid(x); % malla de puntos medios f=X+Y-Z; % valores de la función sobre la malla sum(f(:)) % suma de Riemann (el volumen de cada subcaja es 1)Esta suma es una aproximación de la integral triple de $f(x,y,z)$ sobre la caja. El valor de esa integral también puede obtenerse en el ordenador, escribiendo
syms x y z % se declaran estas variables simbólicas int(int(int(x+y-z,z,0,2),y,0,2),x,0,2) % cálculo de la integral
Ejercicio 4
Sea $H$ la caja $[0,1]\times[0,1]\times[0,1]$. Sea $R_n$ la sección correspondiente al plano $y=\frac{1}{n}$ donde $n$ toma los valores naturales desde 2 hasta 10. ¿Cuántas secciones $R_n$ hay? Representa $H$ y las secciones $R_n$.
Solución
Obviamente, hay 9 secciones, una para cada número natural entre 2 y 10, ambos incluidos.
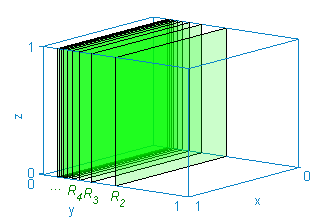
Se pueden dibujar a mano o también en el ordenador, escribiendo:

Se pueden dibujar a mano o también en el ordenador, escribiendo:
for n=2:10 % ciclo para dibujar las secciones
hold on
fill3([0 0 1 1], (1/n)*ones(1,4),[0 1 1 0],'g') % cada sección es un cuadrado
alpha(.2) % transparencia
end
axis([0 1 0 1 0 1]) % tamaño de los ejes
box on % incluye caja
xlabel('x');ylabel('y');zlabel('z'); % etiquetas de los ejes
hold off
Ejercicio 5
Para la caja $H[0,1]\times[0,1]\times[0,1]$ y las secciones $R_n$, correspondientes a $n$ entre 2 y 10 (ver ejercicio anterior), sea $f(x,y,z)$ una función definida en $H$ que es acotada en todo $H$ y continua salvo en las secciones $R_n$. ¿Está garantizada la existencia de la integral de $f$ sobre $H$?
Pista
Solución
Debes tener en cuenta sobre cuántas superficies incluidas en $H$ no es continua $f$ y cómo son esas superficies.
Sí está garantizada la existencia de $f$ sobre $H$, pues cada sección $R_n$ es una superficie suave y hay un número finito de ellas.
Ejercicio 6
En la misma caja $H=[0,1]\times[0,1]\times[0,1]$, supón ahora que la función $f$ fuera discontinua en todas las secciones correspondientes a los planos $y=\frac{1}{r}$ para $r$ racional entre 2 y 10. ¿Estaría garantizada ahora la existencia de la integral de $f$ sobre $H$?
Pista
Solución
Debes tener en cuenta sobre cuántas superficies incluidas en $H$ no es continua $f$ y cómo son esas superficies.
$f$ es discontinua en un número infinito de superficies contenidas en $H$, por lo que no está garantizada la integrabilidad.
Ejercicio 7
Verdadero o falso: Si $H_1$ y $H_2$ son dos cajas, tales que $H_1\subset H_2$ (es decir, todos los puntos de $H_1$ están en $H_2$), entonces la integral triple de una función sobre $H_1$ es necesariamente menor que la integral de la misma función sobre $H_2$.
Solución
Falso. La relación entre la integral sobre $H_1$ y la integral sobre $H_2$ dependerá del signo que tome la función sobre la parte de $H_2$ que no está incluida en $H_1$. Por ejemplo, si $H_1=[0,1]\times[0,1]\times[0,1]$ y $H_2=[0,2]\times[0,2]\times[0,2]$ y sobre ellas se define la función $f(x,y,z)=-xyz$, la integral de $f$ en la parte de $H_2$ que no es $H_1$ es negativa, con lo cual, la integral sobre $H_1$ será mayor que la integral sobre $H_2$. En la figura vemos unas secciones de $H_2$ y $H_1$ coloreadas según el valor de $f(x,y,z)=-xyz$.
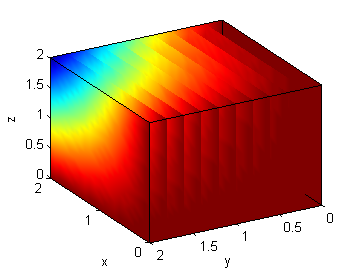
Esta figura se ha realizado con el código

Esta figura se ha realizado con el código
[x,y,z] = meshgrid(0:.1:2);
v = -x.*y.*z;
xslice = 2; yslice = (0:10)/5; zslice = 0;
slice(x,y,z,v,xslice,yslice,zslice)
colormap jet
shading interp
xlabel('x');ylabel('y');zlabel('z');
box on
view([-120,32])
Ejercicio 8
$S$ es la porción del plano $6x+3y+2z=6$ que se encuentra en el primer octante:
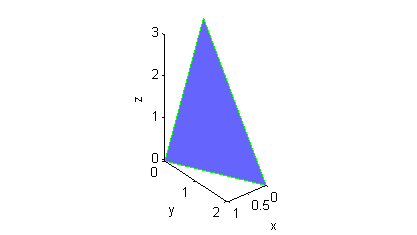
Representa y escribe en notación de conjunto

Representa y escribe en notación de conjunto
- la proyección de $S$ en el plano $XY$: $R_{xy}$,
- la proyección de $S$ en el plano $XZ$: $R_{xz}$,
- la proyección de $S$ en el plano $YZ$: $R_{yz}$.
Pista
Solución
El plano $6x+3y+2z=6$ corta a los planos coordenados en tres segmentos rectos, respectivamente. Encuentra esas rectas en los planos coordenados para hallar las proyecciones.
Las proyecciones son
$$R_{xy}=\{(x,y) /\, 0\leq x\leq 1,\, 0\leq y\leq 2(1-x)\}$$
$$R_{xz}=\{(x,z) /\, 0\leq x\leq 1,\, 0\leq z\leq 3(1-x)\}$$
$$R_{yz}=\{(y,z) /\, 0\leq y\leq 1,\, 0\leq z\leq 3\left(1-\frac{y}{2}\right)\}$$
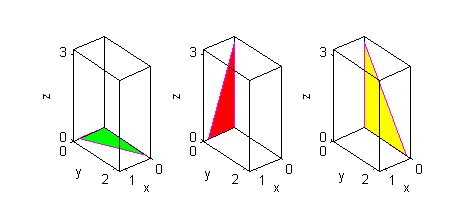
Estas proyecciones son fáciles de trazar a mano. Si quieres dibujarlas en el ordenador puedes hacerlo con el código siguiente, con el que también se dibuja, en otra figura, la porción de plano:

Estas proyecciones son fáciles de trazar a mano. Si quieres dibujarlas en el ordenador puedes hacerlo con el código siguiente, con el que también se dibuja, en otra figura, la porción de plano:
figure(1)
subplot(1,3,1)
fill3([1 0 0],[0 2 0],[0 0 0],'g', 'EdgeColor','m')
axis equal
xlabel('x');ylabel('y');zlabel('z');
view([141,32])
axis([0 1.2 0 2.2 0 3.2])
subplot(1,3,2)
fill3([1 0 0],[0 0 0],[0 0 3],'r', 'EdgeColor','m')
axis equal
xlabel('x');ylabel('y');zlabel('z');
view([141,32])
axis([0 1.2 0 2.2 0 3.2])
subplot(1,3,3)
fill3([0 0 0],[0 2 0],[0 0 3],'y', 'EdgeColor','m')
axis equal
xlabel('x');ylabel('y');zlabel('z');
view([141,32])
axis([0 1.2 0 2.2 0 3.2])
figure(2)
fill3([1 0 0],[0 2 0],[0 0 3],'b', 'EdgeColor','m')
axis equal
xlabel('x');ylabel('y');zlabel('z');
alpha(.6)
view([141,32])
Ejercicio 9
Si $H$ es una región del espacio, $x$, $y$ y $z$ son longitudes medidas en cm. y la función $g(x,y,z)$ es una densidad de masa (medida en gr$/\mbox{cm}^3$), indica en qué unidades se mide
- $dx\, dy\, dz$
- $g(x,y,z)\, dV$
- $\int\!\!\int\!\!\int_H g(x,y,z)\, dV$
- $\frac{\int\!\!\int\!\!\int_H g(x,y,z)\, dV}{\mbox{Volumen} (H)}$
Solución
- $dx\, dy\, dz$ se mide en $\mbox{cm}^3$,
- $g(x,y,z)\, dV$ se mide en gr., pues es la unidad elegida para la masa,
- $\int\!\!\int\!\!\int_H g(x,y,z)\, dV$ se mide en gr., igualmente es una masa,
- $\frac{\int\!\!\int\!\!\int_H g(x,y,z)\, dV}{\mbox{Volumen} (H)}$ es una densidad, luego en gr$/\mbox{cm}^3$.
Ejercicio 10
Si $H$ es una región del espacio, $x$, $y$ y $z$ son longitudes medidas en cm. y la función $g(x,y,z)$ es la temperatura en cada punto (medida en $^o$C), indica en qué unidades se mide
- $g(x,y,z)\, dV$
- $\int\!\!\int\!\!\int_H g(x,y,z)\, dV$
- $\frac{\int\!\!\int\!\!\int_H g(x,y,z)\, dV}{\mbox{Volumen} (H)}$
Solución
- $g(x,y,z)\, dV$ se mide en $^o\mbox{Ccm}^3$,
- igualmente, $\int\!\!\int\!\!\int_H g(x,y,z)\, dV$ se mide en $^o\mbox{Ccm}^3$,
- $\frac{\int\!\!\int\!\!\int_H g(x,y,z)\, dV}{\mbox{Volumen} (H)}$ es una temperatura, se medirá en $^o$C.