Ejercicios preliminares e instantáneos. Integral múltiple (primera parte)
Ejercicio 1
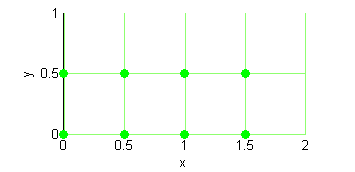
Dibuja la partición del rectángulo $R=[0,2]\times[0,1]$ en $4\times 2$ cuadrados iguales. Escribe todos los puntos inferiores izquierdos de esa partición. Escribe la fórmula, en función de dos índices, de sus abscisas y de sus ordenadas.
Solución
Los puntos inferiores izquierdos son $$\left(0,0\right ),\ \left(\frac{1}{2},0\right),\ \left(1,0\right), \ \left(\frac{3}{2},0\right),\ \left(0,\frac{1}{2}\right),\ \left(\frac{1}{2},\frac{1}{2}\right),\ \left(1,\frac{1}{2}\right),\ \left(\frac{3}{2},1\right)$$ Responden a la fórmula $\left(\frac{i}{2},\frac{j}{2}\right )$ con $i=0,\, 1,\, 2,\, 3$ y $j=0,\, 1$.

Ejercicio 2
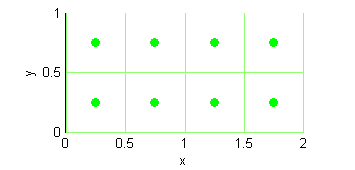
Dibuja la partición del rectángulo $R=[0,2]\times[0,1]$ en $4\times 2$ cuadrados iguales. Escribe todos los puntos medios de cada cuadrado de la partición. Escribe la fórmula, en función de dos índices, de sus abscisas y de sus ordenadas.
Solución
Los puntos medios son $$\left(\frac{1}{4},\frac{1}{4}\right ),\ \left(\frac{3}{4},\frac{1}{4}\right),\ \left(\frac{5}{4},\frac{1}{4}\right), \ \left(\frac{7}{4},\frac{1}{4}\right),\ \left(\frac{1}{4},\frac{3}{4}\right),\ \left(\frac{3}{4},\frac{3}{4}\right),\ \left(\frac{5}{4},\frac{3}{4}\right),\ \left(\frac{7}{4},\frac{3}{4}\right)$$ Responden a la fórmula $\left(\frac{2i-1}{4},\frac{2j-1}{4}\right )$ con $i=1,\, 2,\, 3,\, 4$ y $j=1,\, 2$ o bien
$\left(\frac{1}{4}+\frac{i}{2},\frac{1}{4}+\frac{j}{2}\right )$ con $i=0,\, 1,\, 2,\, 3$ y $j=0,\, 1$.

Ejercicio 3
Escribe la suma de Riemann de la función $z=f(x,y)=x-y$ en el rectángulo $R=[0,2]\times[0,1]$ tomando la partición en $4\times 2$ cuadrados iguales y el punto medio en cada subrectángulo de la partición. Esta suma es una aproximación de la integral de $f$ sobre $R$.
Pista
Solución
La suma de Riemann es la suma de los valores de la función $z=f(x,y)$ en los puntos elegidos (en este caso los puntos medios) multiplicados cada uno de ellos por el área del subrectángulo correspondiente; por ejemplo, el primer sumando será el valor de $f(x,y)$ en el punto $\left(\frac{1}{4},\frac{1}{4}\right )$ multiplicado por el área del cuadrado del cual hemos tomado $\left(\frac{1}{4},\frac{1}{4}\right )$, esto es, área $1/4$.
En esta figura vemos el valor de la función sobre los puntos elegidos:
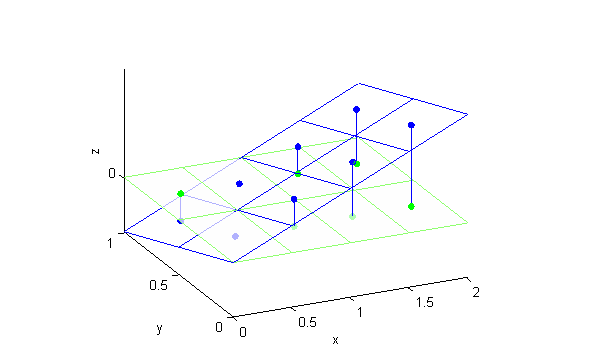
La suma de Riemann es la suma de los volúmenes de los prismas que se forman con esas 'alturas':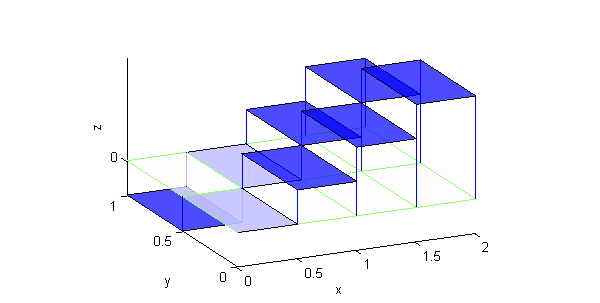
El valor de esta suma de Riemann es 1. El código para evaluarla en el ordenador podría ser:

La suma de Riemann es la suma de los volúmenes de los prismas que se forman con esas 'alturas':

El valor de esta suma de Riemann es 1. El código para evaluarla en el ordenador podría ser:
x=1/4+(0:3)/2; % abscisas de los puntos medios
y=1/4+(0:1)/2; % ordenadas de los puntos medios
[X,Y]=meshgrid(x,y); % malla de puntos medios
Z=X-Y; % valores de la función sobre la malla
sum(Z(:))/4 % suma de Riemann
El valor exacto de la integral es fácil de obtener a mano; puedes hacerlo para comprobar cuánto error se ha cometido en la aproximación con la suma de Riemann. Si quieres hacerlo en el ordenador puedes escribir:
syms x y % declaramos x e y como variables simbólicas
int(int(x-y,y,0,1),x,0,2) % cálculo de la integral de x-y en [0,2]x[0,1]
Ejercicio 4
Verdadero o falso: Una función de dos variables tiene que ser continua en un rectángulo $R$ para que sea integrable en él.
Solución
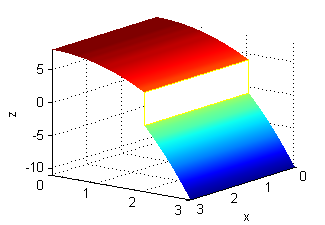
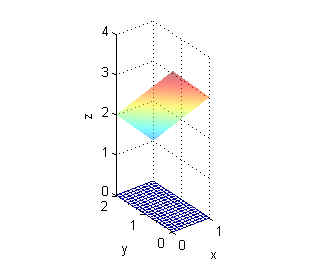
Falso. También está asegura la integrabilidad si es discontinua sobre un número finito de curvas suaves, siempre que permanezca acotada. Por ejemplo la superficie que se muestra en la figura, es la gráfica de una función integrable en el rectángulo $[0,3]\times[0,3]$, a pesar de que es discontinua en todo el segmento $y=2$.

Ejercicio 5
Verdadero o falso: La integral sobre un rectángulo del producto de dos funciones es el producto de las integrales dobles de cada factor.
Solución
Falso, al igual que la suma de productos no es el producto de la suma. Recuerda que la integral es el límite de las sumas de Riemann. Como contraejemplo, piensa en $f(x,y)=1$ y $g(x,y)=1$: la integral de $f(x,y)g(x,y)=1$ sobre el rectángulo $R=[0,2]\times[0,1]$ es el área de $R$, es decir, 2; la integral de $f(x,y)$ también es el área de $R$, y lo mismo ocurre con la integral de $g(x,y)$; pero desde luego 2 no es igual a 4.
Ejercicio 6
Dados los rectángulos $R_1=[0,2]\times[0,2]$ y $R_2=[0,2]\times[1,3]$ y las integrales
$$I_1=\int\!\!\int_{R_1} f(x,y)\, dA \ \ ,\ \ I_2=\int\!\!\int_{R_2} f(x,y)\, dA \ \ ,\ \ I_3=\int\!\!\int_{R_1\cup R_2} f(x,y)\, dA$$ Para cada uno de los supuestos siguientes, da una condición para $f(x,y)$ que lo haga cierto
- $I_1+I_2>I_3$
- $I_1+I_2=I_3$
- $I_1+I_2< I_3$
Pista
Solución
En la unión de dos rectángulos con una parte común, esa parte está sólo una vez. Además, recuerda que la integral de una función positiva sobre un rectángulo es necesariamente un número positivo y de la misma forma, la integral de una función que es negativa en todos los puntos de un rectángulo resulta necesariamente un número negativo.
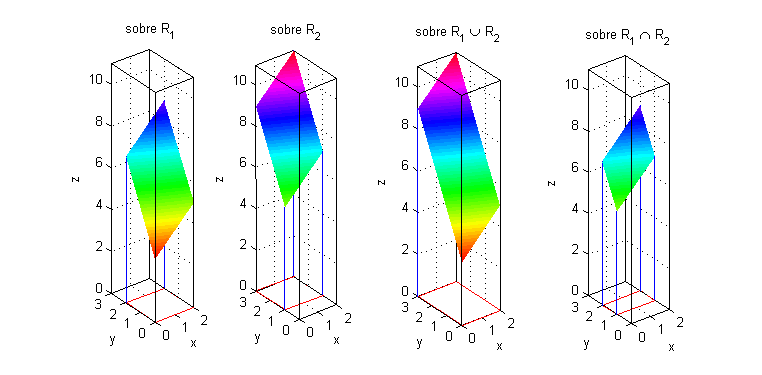
$R=[0,2]\times[1,2]$ es la parte común a $R_1$ y $R_2$: esto se escribe $R=R_1\cap R_2$. En $I_1+I_2$ se está integrando dos veces sobre $R=R_1\cap R_2$, mientras que en $I_3$ sólo una. Por tanto,
- $I_1+I_2>I_3$ si por ejemplo $f(x,y)$ es positiva en $R$: el volumen correspondiente a $R_1\cap R_2$ (figura de la derecha) está dos veces en $I_1+I_2$ y sólo una vez en $I_3$
- $I_1+I_2=I_3$ si por ejemplo $f(x,y)$ es nula en $R$
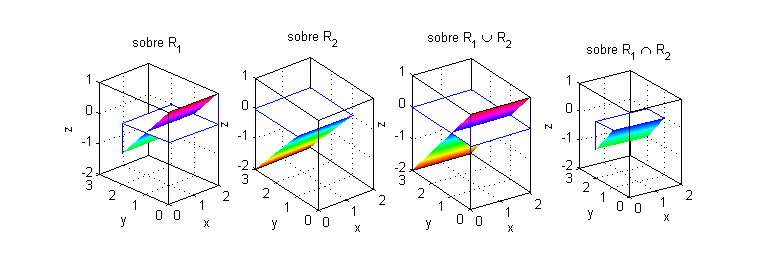
- $I_1+I_2<I_3$ si por ejemplo $f(x,y)$ es negativa en $R$: la integral de $f(x,y)$ sobre $R$ (figura de la derecha) es negativa y está dos veces en $I_1+I_2$ y sólo una vez en $I_3$
Ejercicio 7
Dibuja en una figura, en el plano ${\bf R}^2$, la gráfica de $x^2+y^2=1$. Dibuja en otra figura, en el espacio ${\bf R}^3$, la gráfica de $x^2+y^2=1$.
Solución
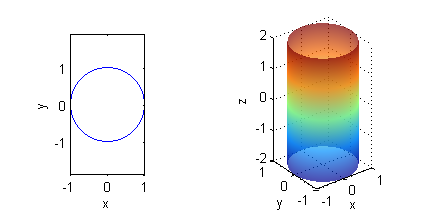
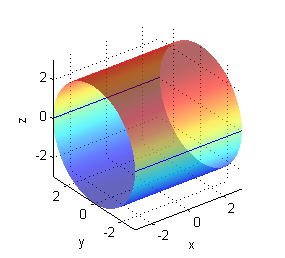
La gráfica de $x^2+y^2=1$ en el plano es la circunferencia de centro $(0,0)$ y radio 1. En el espacio, $x^2+y^2=1$ es un cilindro circular recto; sólo podemos dibujar una parte, por ejemplo la correspondiente a $-2\leq z\leq 2$

t=0:pi/20:2*pi; % valores del ángulo
subplot(1,2,1)
plot(cos(t),sin(t)) % trazado de la circunferencia
xlabel('x');ylabel('y');axis equal
subplot(1,2,2)
[T,Z]=meshgrid(t,-2:2); % malla para dibujar el cilindro
surf(cos(T),sin(T),Z); % trazado del cilindro
shading interp
alpha(.7)
Ejercicio 8
Dibuja en ${\bf R}^3$, en diferentes figuras, una porción de las superficies $y=x^2$, $z=y^2$ y $z=x^2$.
Solución
- $y=x^2$ es un cilidro parabólico, cada sección por planos $z$ constante repite la misma parábola
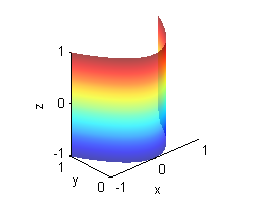
- $z=y^2$ es un cilidro parabólico, cada sección por planos $x$ constante repite la misma parábola
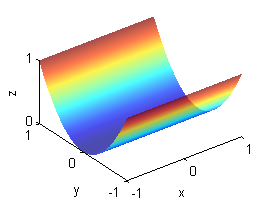
- $z=x^2$ es un cilidro parabólico, cada sección por planos $y$ constante repite la misma parábola
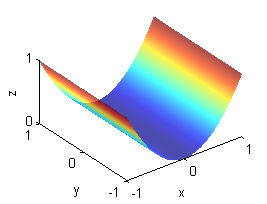
function cilindros(apartado)
[X,Y]=meshgrid(-1:.1:1); % malla de puntos
figure(apartado)
switch apartado
case 1
surf(X,X.^2,Y) % cilindro parabólico y=x^2
case 2
surf(X,Y,Y.^2) % cilindro parabólico z=y^2
case 3
surf(X,Y,X.^2) % cilindro parabólico z=x^2
end
shading interp
alpha(.7)
axis equal
xlabel('x');ylabel('y');zlabel('z');
end
Ejercicio 9
En cada caso, describe con palabras y representa gráficamente el lugar geométrico de los puntos que están en las dos superficies indicadas:
- $z=4-x^2$ y $x=1$
- $z=4-x^2$ e $y=1$
- $z=4-x^2$ y $z=3$
Solución
- Es la recta $x=1$ en $z=3$:
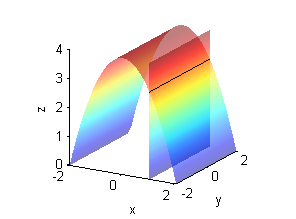
- Es la parábola $z=4-x^2$ en $y=1$:
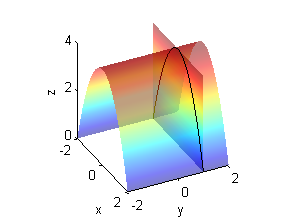
- Es el par de rectas $z=3$ en $x=1$ y $z=3$ en $x=-1$:
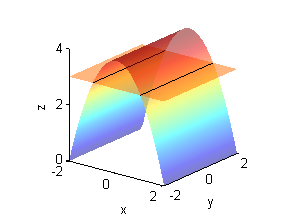
Ejercicio 10
Marca en el plano ${\bf R}^2$:
- la región infinita dada por $y\geq 3x$;
- la región infinita dada por $y\leq -2x$;
- la región infinita dada por $3x\leq y\leq -2x$;
- la región finita dada por $3x\leq y\leq -2x$, con $x\geq -2$.
Solución
- la región infinita dada por $y\geq 3x$:
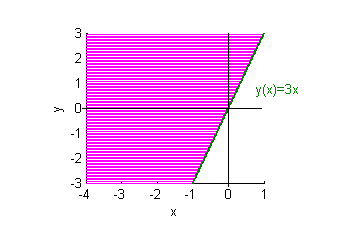
- la región infinita dada por $y\leq -2x$:
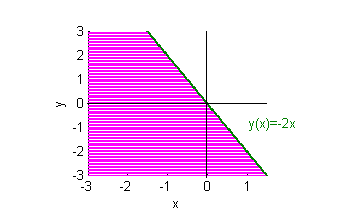
- la región infinita dada por $3x\leq y\leq -2x$:
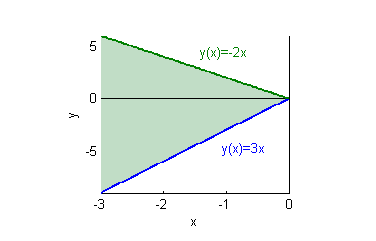
- la región finita dada por $3x\leq y\leq -2x$, con $x\geq -2$:
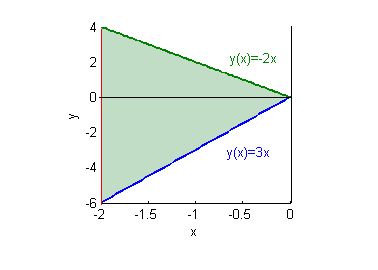
Ejercicio 11
Marca en el plano ${\bf R}^2$ una porción de las regiones infinitas dadas por
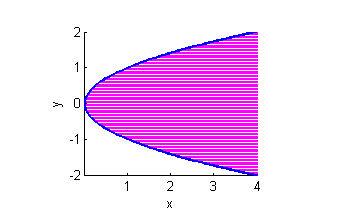
- $x\geq y^2$
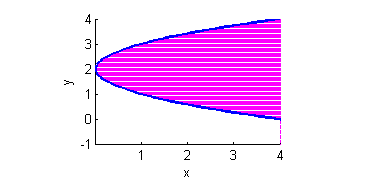
- $x\geq (y-2)^2$
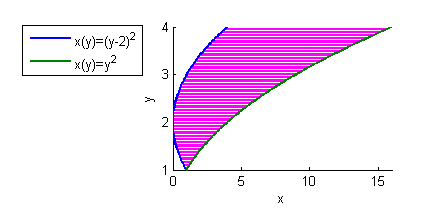
- $(y-2)^2\leq x\leq y^2$
Solución
- $x\geq y^2$:
- $x\geq (y-2)^2$:
- $(y-2)^2\leq x\leq y^2$:
Ejercicio 12
¿Cuáles de las siguientes funciones $z=f(x,y)$ son positivas en el rectángulo $R=[0,1]\times [0,2]$?
- $z=4-x-y$
- $z=2(x+y-1)$
- $z=9-(x^2+y^2)$
Pista
Solución apartado a.
Mira a ver si la curva $f(x,y)=0$ toca al rectángulo $R$.
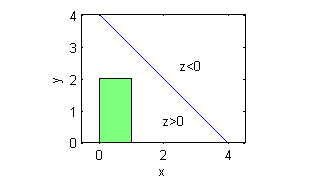
$z=4-x-y$ se anula en $x+y=4$;
todo $R$ está en la región $x+y<4$, donde $z=4-x-y$ es positiva:


Apartado b: $z=2(x+y-1)$
Solución apartado b.
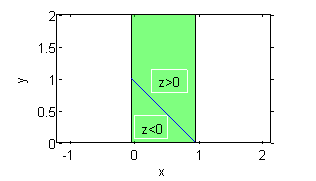
La recta $x+y=1$ atraviesa $R$: $z=2(x+y-1)$ es positiva sólo en la parte de $R$ que queda encima de la recta $x+y=1$:
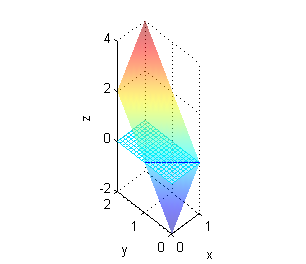


Apartado c: $z=9-(x^2+y^2)$
Solución
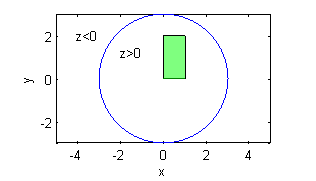
$R$ está incluido entero en la región $x^2+y^2<9$, donde $z=9-(x^2+y^2)$ es positiva:


Ejercicio 13
¿Dónde cortan las siguientes superficies al plano $z=0$?
- $z=1+x^2+y^2$
- $z=1-x^2-2y^2$
- $z=\sqrt{x^2+y^2}-1$
- $x^2+y^2=9$
- $x^2+z^2=9$
- $z^2+y^2=9$
Solución
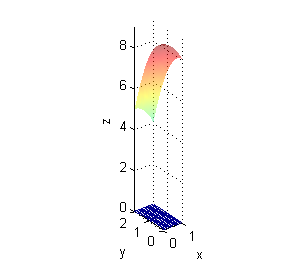
- $z=1+x^2+y^2$ es siempre positiva, de hecho es siempre mayor o igual que 1; no se corta con el plano $z=0$:
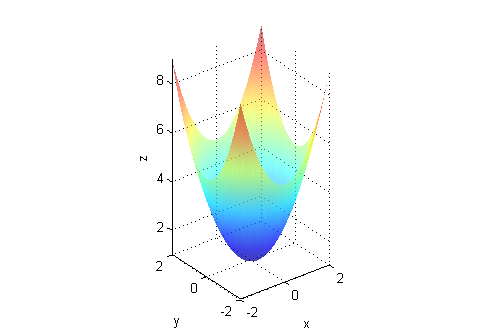
- $z=1-x^2-2y^2$ corta al plano $z=0$ en la elipse $\frac{x^2}{2}+y^2=\frac{1}{2}$:
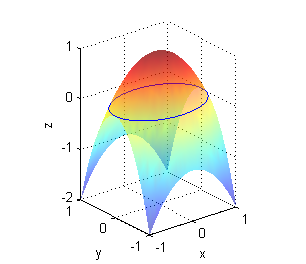
- $z=\sqrt{x^2+y^2}-1$ corta al plano $z=0$ en la circunferencia $x^2+y^2=1$:
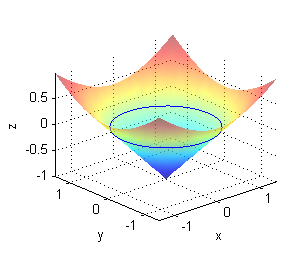
- $x^2+y^2=9$ corta al plano $z=0$ en la circunferencia $x^2+y^2=9$:
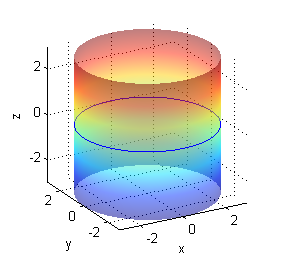
- $x^2+z^2=9$ corta al plano $z=0$ en las rectas $x=-3$ y $x=3$:
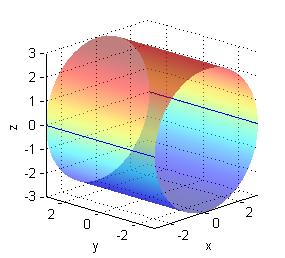
- $z^2+y^2=9$ corta al plano $z=0$ en las rectas $y=-3$ e $y=3$:
Ejercicio 14
Si $R$ es una región del plano, $x$ e $y$ son longitudes medidas en cm., $r$ y $\theta$ son las correspondientes coordenadas polares y la función $g(x,y)$ es una densidad superficial (medida en gr$/\mbox{cm}^2$) indica en qué unidades se mide
- $dx\, dy$
- $g(x,y)\, dA$
- $\int\!\!\int_R g(x,y)\, dA$
- $\frac{\int\!\!\int_R g(x,y)\, dA}{\mbox{Área} (R)}$
- $dr$
- $dr\, d\theta$
- $r\, dr\, d\theta$
- $g(r\cos\theta ,r\mbox{sen} \theta)r\, dr\, d\theta$
Pista
Solución
Recuerda que la diferencial de una variable no es más que una diferencia entre valores de esa variable; por lo tanto si, por ejemplo, la variable es una longitud, su diferencial también lo será.
- $dx\, dy$ se mide en $\mbox{cm}^2$, pues es un área;
- $g(x,y)\, dA$ se mide en gr, es una masa;
- $\int\!\!\int_R g(x,y)\, dA$ también en gr, sigue siendo una masa;
- $\frac{\int\!\!\int_R g(x,y)\, dA}{\mbox{Área} (R)}$ se mide en gr$/\mbox{cm}^2$, pues es la unidad elegida para la densidad;
- $dr$ se mide en cm., pues es en lo que se está midiendo $r$;
- $dr\, d\theta$ también en cm., pues $\theta$ es adimensional;
- $r\, dr\, d\theta$ se mide en $\mbox{cm}^2$;
- $g(r\cos\theta ,r\mbox{sen} \theta)r\, dr\, d\theta$ se mide en gr, es una masa.
Ejercicio 15
Encuentra y representa la proyección en el plano $XY$ de cada una de las siguientes superficies
- $x^2+z^2=2$ en $z>0$ para $1\leq y \leq 2$
- $z=x^2+y^2$ en $1\leq z \leq 4$
- $z=1-\sqrt{x^2+y^2}$ en $-2\leq z \leq 0$
Solución
Los códigos que se incluyen, además de representar la proyección también trazarán la superficie.
- La proyección es el rectángulo $R_{xy}=[-\sqrt{2},\sqrt{2}]\times [1,2]$:
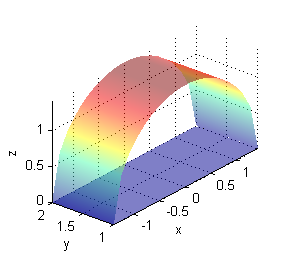
x=linspace(-sqrt(2)+10^(-7),sqrt(2)-10^(-7),20); [X,Y]=meshgrid(x,1:2); surf(X,Y,sqrt(2-X.^2)) % trazado de la superficie hold on surf(X,Y,zeros(size(X))) % dibujo de la proyección shading interp hold off axis equal;xlabel('x');ylabel('y');zlabel('z');alpha(.5) - La proyección es la corona circular de centro $(0,0)$ y radios $1$ y $2$:
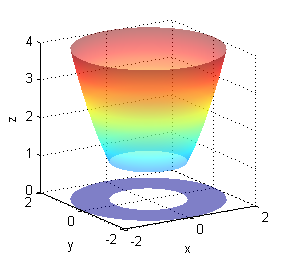
[R,T]=meshgrid(1:.05:2,0:pi/20:2*pi); surf(R.*cos(T),R.*sin(T),R.^2) % trazado de la superficie hold on surf(R.*cos(T),R.*sin(T),zeros(size(R))) % dibujo de la proyección shading interp hold off axis equal;xlabel('x');ylabel('y');zlabel('z');alpha(.5) - La proyección es la corona circular de centro $(0,0)$ y radios $1$ y $3$:
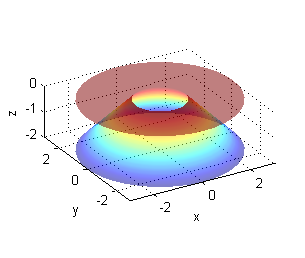
[R,T]=meshgrid(1:.05:3,0:pi/20:2*pi);
surf(R.*cos(T),R.*sin(T),1-R) % trazado de la superficie
hold on
surf(R.*cos(T),R.*sin(T),zeros(size(R))) % dibujo de la proyección
shading interp
hold off
axis equal;xlabel('x');ylabel('y');zlabel('z');alpha(.5)
Ejercicio 16
Encuentra y representa la proyección en el plano $XZ$ de cada una de las siguientes superficies
- $y=3-(x^2+z^2)$ para $2\leq y\leq 3$
- $x^2+y^2=4$ para $1\leq y\leq 2$
- $x^2+y^2+z^2=1$ para $z\geq 1-y$
Solución
Los códigos que se incluyen, además de representar la proyección también trazarán la superficie.
- La proyección es el círculo de centro $(0,0)$ y radio 1:
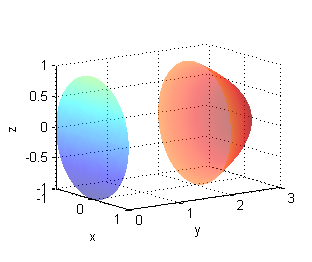
[R,T]=meshgrid(0:.1:1,0:pi/20:2*pi); surf(R.*cos(T),3-R.^2,R.*sin(T),3-R.^2) % trazado de la superficie hold on surf(R.*cos(T),zeros(size(R)),R.*sin(T)) % dibujo de la proyección shading interp hold off axis equal;xlabel('x');ylabel('y');zlabel('z');alpha(.5) - La proyección es la banda infinita $-\sqrt{3}\leq x\leq \sqrt{3}$, $z\in{\bf R}$; en la figura se ha tomado $z$ entre $-2$ y $2$:
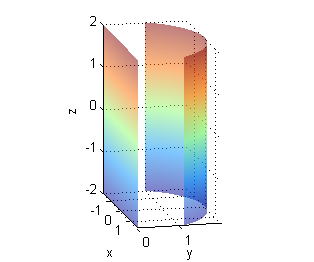
[X,Z]=meshgrid(-sqrt(3):.1:sqrt(3),-2:2); surf(X,sqrt(4-X.^2),Z) % trazado de la superficie hold on surf(X,zeros(size(X)),Z) % dibujo de la proyección shading interp hold off axis equal;xlabel('x');ylabel('y');zlabel('z');alpha(.5) - La proyección es el interior de la elipse $x^2+2\left(z-\frac{1}{2}\right)^2=\frac{1}{2}$:
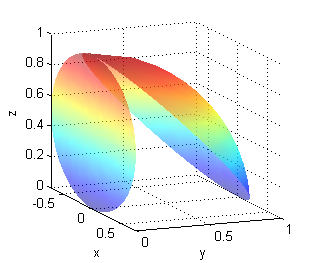
[R,T]=meshgrid(0:.1:1,0:pi/20:2*pi); X=R.*cos(T)/sqrt(2); Z=.5*(1+R.*sin(T)); % trazado de la superficie surf(X,sqrt(1-X.^2-Z.^2),Z) hold on surf(X,zeros(size(X)),Z) % dibujo de la proyección shading interp hold off axis equal;xlabel('x');ylabel('y');zlabel('z');alpha(.5)
Ejercicio 17
Encuentra el argumento (variable $\theta$ de polares) de las siguientes semirrectas
- $y=x$ en $x>0$
- $y=-x$ en $x<0$
- $y=0$ en $x<0$
- $x=0$ en $y>0$
- $x=0$ en $y<0$
- $y=\sqrt{3}x$ en $x>0$
- $y=-\sqrt{3}x$ en $x>0$
- $y=\frac{x}{\sqrt{3}}$ en $x<0$
- $y=-\frac{x}{\sqrt{3}}$ en $x<0$
Pista
Solución
Recuerda que el argumento de la semirecta de ecuación $y=kx$ es el ángulo $\theta=\mbox{arctg}\, \frac{y}{x}$; si los ángulos se toman entre $-\pi$ y $\pi$, debe cumplirse que $\mbox{signo}\, \theta=\mbox{signo}\, y$
- $y=x$ en $x>0$ es $\theta=\pi/4$:
- $y=-x$ en $x<0$ es $\theta=3\pi/4$:
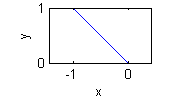
- $y=0$ en $x<0$ es $\theta=\pi$:
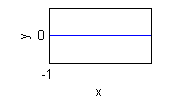
- $x=0$ en $y>0$ es $\theta=\pi/2$:
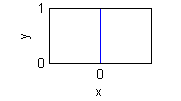
- $x=0$ en $y<0$ es $\theta=-\pi/2$ o $\theta=3\pi/2$:
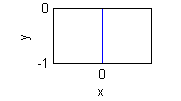
- $y=\sqrt{3}x$ en $x>0$ es $\theta=\pi/3$:
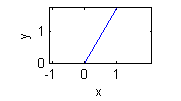
- $y=-\sqrt{3}x$ en $x>0$ es $\theta=-\pi/3$ o $\theta=5\pi/3$:
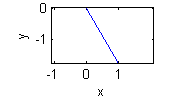
- $y=\frac{x}{\sqrt{3}}$ en $x<0$ es $\theta=-5\pi/6$ o $\theta=7\pi/6$:
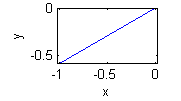
- $y=-\frac{x}{\sqrt{3}}$ en $x<0$ es $\theta=5\pi/6$:
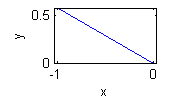
Ejercicio 18
Halla las derivadas parciales de las siguientes funciones respecto de su primera variable:
- $u(x,y)=x/y$
- $x(s,t)=s^2\cos (st)$
- $y(u,v)=u+e^{u+v}$
Pista
Solución
Recuerda que para hallar la derivada parcial de $z=f(x,y)$ respecto de $x$, derivamos $f$ tomando la $y$ como una constante.
- $u'_x(x,y)=\frac{1}{y}$; el código para hacer esta derivada en el ordenador sería
syms x y % declara las variables x e y como simbólicas diff(x/y,x) % deriva la función x/y respecto de x
- $x'_s(s,t)=2s\cos (st)-ts^2\mbox{sen} (st)$
- $y'_u(u,v)=1+e^{u+v}$
Ejercicio 19
Halla las derivadas parciales de las funciones del ejercicio anterior
- $u(x,y)=x/y$
- $x(s,t)=s^2\cos (st)$
- $y(u,v)=u+e^{u+v}$
Solución
- $u'_y(x,y)=\frac{-x}{y^2}$; el código para hacer esta derivada en el ordenador sería
syms x y % declara las variables x e y como simbólicas diff(x/y,y) % deriva la función x/y respecto de y
- $x'_t(s,t)=-s^3\mbox{sen} (st)$
- $y'_v(u,v)=e^{u+v}$
Ejercicio 20
Divide $p(x,y)$ entre $q(x,y)$ para los siguientes casos:
- $p(x,y)=2x^3+x^2y(y-2)+xy(1-y^2)-y^2$, $q(x,y)=x-y$
- $p(x,y)=x^4-x^3(y+1)+3x^2y-xy(y+1)+2y^2$, $q(x,y)=x^2+y$
Pista
Solución
Para dividir polinomios como éstos, que tienen dos variables, hemos de pensar en ellos como funciones de una de ellas y la otra tratarla, de cara a la división, como si fuera una constante. Por ejemplo, el polinomio $y^2-2-3yx$ podemos escribirlo ordenado en potencias de $x$: $$-3yx+y^2-2$$
de manera que el coeficiente del primer monomio es $(-3y)$ y el término independiente es $y^2-2$
o podemos expresarlo ordenado en potencias de $y$:
$$y^2-3xy-2$$ de forma que el coeficiente del monomio de grado dos es $1$, el coeficiente del monomio de grado 1 es $-3x$ y el coeficiene del término independiente es $-2$. Si tenemos que dividir $y^2-2-3yx$ entre $x-y$, podemos tomar ambos ordenados en potencias de $x$, considerando la $y$ como constante:
$$\frac{-3yx+y^2-2}{x-y}=-3y-2\frac{y^2+1}{x-y}$$
o podemos ordenar ambos en potencias de $y$ considerando la $x$ como constante:
$$\frac{y^2-3xy-2}{-y+x}=-y+2x-2\frac{x^2+1}{-y+x}$$
- $\frac{p(x,y)}{q(x,y)}=2x^2+y^2x+y$
- $\frac{p(x,y)}{q(x,y)}=x^2-x(y+1)+2y$