Extremos y puntos de inflexión

Sea $y=f(x)$ una función definida en un dominio $D$ y sea $a$ un punto de $D$. Se dice que

• $f(a)$ es el valor máximo absoluto o global de $f$ en $D$ si $f(a)> f(x)$ para cualquier $x$ de $D$, $x\neq a$;

• Si se invierte la desigualdad, $f(a)$ es el mínimo absoluto o global de $f$ en $D$;

• $f(a)$ es un valor máximo relativo o local (o simplemente $f(a)$ es un máximo relativo) de $f$ en $D$ si existe un intervalo centrado en $a$ contenido en $D$ de manera que $f(a)\geq f(x)$ para cualquier $x$ del intervalo;

• Si se invierte la desigualdad, $f(a)$ es un mínimo relativo o local de $f$ en $D$;

• Un extremo relativo o local es un máximo o un mínimo local;

• $(a,f(a))$ es un punto de inflexión de $f$ si $y=f(x)$ es cóncava hacia arriba a un lado de $a$ y cóncava hacia abajo al otro. Recordamos que una función es cóncava hacia abajo si las tangentes quedan por encima de la gráfica de la función y es cóncava hacia arriba si las tangentes quedan bajo la gráfica de la función.

Análisis local de funciones mediante polinomios de Taylor

Consideremos una función $y=f(x)$ con derivadas hasta el orden $n$ en el punto $a$, entonces podemos escribir $$f(x)=T_n[f(x);a]+o((x-a)^n)$$ Si ocurre que todas las derivadas de $f$ en $a$ son nulas desde el orden 1 hasta el orden $n-1$ (se entiende que $n>1$), $$f'(a)=f''(a)=\ldots=f^{(n-1}(a)=0$$ entonces la expresión anterior queda $$f(x)-f(a)=\frac{f^{(n}(a)}{n!}(x-a)^n+o((x-a)^n)$$ lo que significa que $$\mbox{signo} [f(x)-f(a)]=\mbox{signo} [f^{(n}(a) (x-a)^n]$$ Por tanto

• Si $n$ es par y $f^{(n}(a)>0$, entonces $f(a)$ es un mínimo local, porque $f^{(n}(a) (x-a)^n$ es positivo a la izquierda y a la derecha:

  

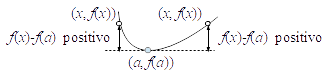
  La recta tangente en $(a,f(a))$ queda por debajo de la gráfica de $y=f(x)$

• Si $n$ es par y $f^{(n}(a)<0$, entonces $f(a)$ es un máximo local, porque $f^{(n}(a) (x-a)^n$ es negativo a la izquierda y a la derecha:

  

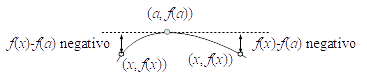
  La recta tangente en $(a,f(a))$ queda por encima de la gráfica de $y=f(x)$

• Si $n$ es impar, $(a,f(a))$ es un punto de inflexión de $f$, porque $f^{(n}(a) (x-a)^n$ tiene signo opuesto a la izquierda y a la derecha:

  

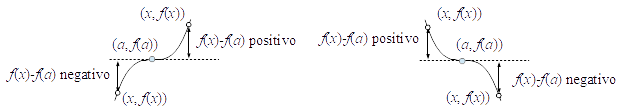
  Si la función pasa de cóncava hacia abajo a cóncava hacia arriba, la recta tangente en $(a,f(a))$ pasa de estar por encima a estar por debajo de la gráfica de $y=f(x)$. Si la gráfica pasa de cóncava hacia arriba a cóncava hacia abajo, la recta tangente pasa de estar por debajo a estar por encima.

Otras situaciones de punto de inflexión

Un punto de inflexión también se da en el caso en que $f'(a)$ no sea nula pero sí lo sea $f''(a)$. En esa situación tendremos que $$f(x)-(f(a)+f'(a)(x-a))=\frac{f'''(a)}{3!}(x-a)^3+o((x-a)^3)$$ por lo que $$\mbox{signo} [f(x)-(f(a)+f'(a)(x-a))]=\mbox{signo} [f'''(a)(x-a)^3]$$ Es decir, si $f'''(a)>0$ la recta tangente en $(a,f(a))$ pasa de estar por encima a estar por debajo de la gráfica de $y=f(x)$ (función pasa de cóncava hacia abajo a cóncava hacia arriba), mientras que si $f'''(a)<0$ la recta tangente pasa de estar por debajo a estar por encima (función pasa de cóncava hacia arriba a cóncava hacia abajo)