Supongamos que de una magnitud sólo se conociera el valor en $n$ puntos igualmente espaciados, pero no la expresión de la función: $$f(x_1),\ f(x_2),\ \ldots,\ f(x_n)$$ Llamamos $h$ al incremento o distancia entre dos $x_k$ consecutivos: $h=\Delta x=x_{k+1}-x_{k}$

El objetivo es calcular la tasa de cambio de esa magnitud $f$ en cualquiera de esos puntos $x_k$. Lo que se obtiene, aplicando polinomios de Taylor, es una aproximación de esa derivada y una cota del error cometido.

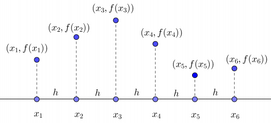
Aproximaciones de primer orden para la derivada primera

Escribimos la fórmula de Taylor de primer grado de $f$ en $x_k$ $$f(x)=f(x_k)+f'(x_k)(x-x_k)+R_1$$

• Si la evaluamos en $x=x_{k+1}$, $$f(x_{k+1})=f(x_k)+f'(x_k)h+R_1 \ \ \ \Rightarrow \ \ \ f'(x_k)=\frac{f(x_{k+1})-f(x_{k})}{h}-\frac{R_1}{h}$$ Puesto que $R_1=o(h)$, $\frac{R_1}{h}$ tiende a cero con $h$, podemos tomar la aproximación $$f'(x_k)\approx \frac{f(x_{k+1})-f(x_{k})}{h}$$ sabiendo que la cota de error es $$|error|=|\frac{R_1}{h}|\leq \frac{M}{2}h$$ donde $M$ es una cota de $|f''(t)|$ en $[x_k,x_{k+1}]$. El cociente con el que aproximamos $f'(x_k)$ es la diferencia progresiva o hacia delante, y proporciona una aproximación para la derivada primera cuyo orden es $h$; esto significa que si, por ejemplo, dividimos por dos la distancia $h$, la cota de error quedará también dividida por 2.

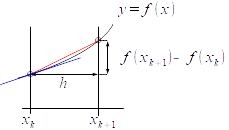
• Si evaluamos la fórmula de Taylor en $x=x_{k-1}$, $$f(x_{k-1})=f(x_k)-f'(x_k)h+R_1\ \ \ \Rightarrow \ \ \ f'(x_k)=\frac{f(x_{k})-f(x_{k-1})}{h}+\frac{R_1}{h}$$ Puesto que $R_1=o(h)$, $\frac{R_1}{h}$ tiende a cero con $h$, podemos tomar la aproximación $$f'(x_k)\approx \frac{f(x_{k})-f(x_{k-1})}{h}$$ sabiendo que la cota de error es $$|error|=|\frac{R_1}{h}|\leq \frac{M}{2}h$$ Esta aproximación para $f'(x_k)$ es la diferencia regresiva o hacia atrás, y proporciona una aproximación de orden $h$ para la derivada primera.

Aproximaciones de segundo orden para la derivada primera

Escribimos la fórmula de Taylor de segundo grado de $f$ en $x_k$ $$ f(x)=f(x_k)+f'(x_k)(x-x_k)+\frac{f''(x_k)}{2}(x-x_k)^2+R_2$$

• Si la evaluamos en $x=x_{k+1}$ y en $x=x_{k-1}$ $$f(x_{k+1})=f(x_k)+f'(x_k)h+\frac{f''(x_k)}{2}h^2+O(h^3)$$ $$f(x_{k-1})=f(x_k)-f'(x_k)h+\frac{f''(x_k)}{2}h^2+O(h^3)$$ las restamos y despejamos $f'(x_k)$, $$f'(x_k)=\frac{f(x_{k+1})-f(x_{k-1})}{2h}-\frac{O(h^3)}{2h}$$ Puesto que el término $\frac{O(h^3)}{2h}$ es un $O(h^2)$, podemos tomar la aproximación $$f'(x_k)\approx \frac{f(x_{k+1})-f(x_{k-1})}{2h}$$

  

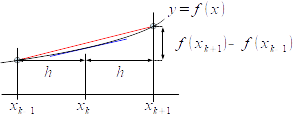
  sabiendo que la cota de error es un infinitésimo de orden 2, es decir, del mismo orden que $h^2$. Esto significa que si, por ejemplo, dividimos por dos la distancia $h$, la cota de error quedará dividida por 4. Esta aproximación para $f'(x_k)$ es la diferencia central o centrada.

• Si evaluamos la fórmula de Taylor en $x=x_{k+1}$ y en $x=x_{k+2}$ $$f(x_{k+1})=f(x_k)+f'(x_k)h+\frac{f''(x_k)}{2}h^2+O(h^3)$$ $$f(x_{k+2})=f(x_k)+f'(x_k)2h+\frac{f''(x_k)}{2}(2h)^2+O(h^3)$$ tomamos $4f(x_{k+1})-f(x_{k+2})$ y despejamos $f'(x_k)$, $$f'(x_k)=\frac{-3f(x_k)+4f(x_{k+1})-f(x_{k+2})}{2h}+\frac{O(h^3)}{2h}$$ de donde $$f'(x_k)\approx \frac{-3f(x_k)+4f(x_{k+1})-f(x_{k+2})}{2h}$$ Es la diferencia progresiva o hacia delante de segundo orden.

• De forma análoga obtendremos $$f'(x_k)\approx \frac{3f(x_k)-4f(x_{k-1})+f(x_{k-2})}{2h}$$ que es la diferencia regresiva o hacia atrás de segundo orden.

Al igual que se ha realizado para la primera derivada, también aplicando polinomios de Taylor pueden obtenerse las diferencias finitas aproximantes de la segunda derivada. En las siguientes tablas se recogen todas estas diferencias finitas:

Diferencias finitas para la primera derivada
Hacia delante o progresiva	Primer orden: $f'(x_k)\approx \frac{f(x_{k+1})-f(x_{k})}{h}$
	Segundo orden: $f'(x_k)\approx \frac{-3f(x_{k})+4f(x_{k+1})-f(x_{k+2})}{2h}$
Hacia atrás o regresiva	Primer orden: $f'(x_k)\approx \frac{f(x_k)-f(x_{k-1})}{h}$
	Segundo orden: $f'(x_k)\approx \frac{3f(x_{k})-4f(x_{k-1})+f(x_{k-2})}{2h}$
Central o centrada	Segundo orden: $f'(x_k)\approx \frac{f(x_{k+1})-f(x_{k-1})}{2h}$

Diferencias finitas para la segunda derivada
Hacia delante o progresiva	Primer orden: $f''(x_k)\approx \frac{f(x_{k})-2f(x_{k+1})+f(x_{k+2})}{h^2}$
	Segundo orden: $f''(x_k)\approx \frac{2f(x_{k})-5f(x_{k+1})+4f(x_{k+2})-f(x_{k+3})}{h^2}$
Hacia atrás o regresiva	Primer orden: $f''(x_k)\approx \frac{f(x_{k})-2f(x_{k-1})+f(x_{k-2})}{h^2}$
	Segundo orden: $f''(x_k)\approx \frac{2f(x_{k})-5f(x_{k-1})+4f(x_{k-2})-f(x_{k-3})}{h^2}$
Central o centrada	Segundo orden: $f''(x_k)\approx \frac{f(x_{k+1})-2f(x_k)+f(x_{k-1})}{h^2}$