Enunciado
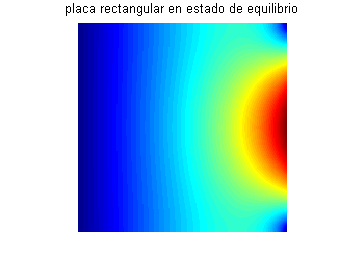
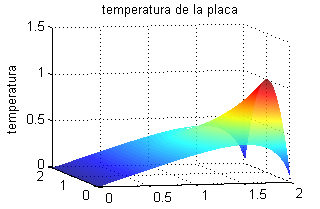
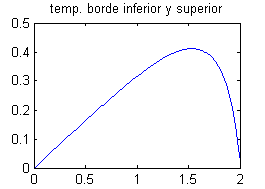
El siguiente problema de contorno es un modelo para la distribución de temperatura (función $u(x,y)$) en estado de equilibrio en una placa cuadrada de lado 2, en cuyos lados inferior y superior no se produce transmisión del calor (en la dirección normal), cuya temperatura en el borde izquierdo es nula y en el borde derecho viene dada por la función $f(y)=y(2-y)$: $$\left\{ \begin{array}{lll} u''_{xx}+u''_{yy}=0 & ,\ 0<x <2 & , \ 0<y <2\\ u'_y(x,0)=0=u'_y(x,2) & , \ 0\leq x\leq 2 & \\ u(0,y)=0,\ u(2,y)=y(2-y) & & ,\ 0\leq y\leq 2 \\ \end{array}\right.$$ Halla su solución formal aplicando el método de separación de variables.
Resolución
Paso 1
Buscar las funciones de la forma $u(x,y)=X(x)Y(y)$ que verifiquen la ecuación y las condiciones homogéneas: $$u(x,y)=X(x)Y(y) \hspace{.7cm} \Rightarrow \hspace{.7cm} X''(x)Y(y)+X(x)Y''(y)=0 \hspace{.7cm} \Rightarrow \hspace{.7cm} -\frac{X''(x)}{X(x)}=\frac{Y''(y)}{Y(y)}$$ Puesto que $\frac{X''}{X}$ es función de $x$ e $\frac{Y''}{Y}$ es función de $y$, siendo $x$ e $y$ variables independientes entre sí, la única posibilidad de que esa igualdad esa cierta es que sean funciones constantes: $$-\frac{X''(x)}{X(x)}=\frac{Y''(y)}{Y(y)}=-\lambda$$ es decir $$X''(x)-\lambda X(x)=0 \hspace{.7cm} , \hspace{.7cm} Y''(y)+\lambda Y(y)=0$$ Ahora...
Utilizamos las condiciones $u(0,y)=0$ y $u(2,y)=y(2-y)$
No utilizamos ninguna condición
Utilizamos las condiciones $u'_y(x,0)=0=u'_y(x,2)$
Eso significa empezar por el problema para $X(x)$, pero de $X(2)Y(y)=y(2-y)$ no podrás deducir nada para $X(2)$.
Hay que utilizar las condiciones, si no ¿cómo podemos continuar esta resolución?
En efecto, comenzaremos resolviendo el problema para $Y(y)$.
Paso 2
Escribir para $Y(y)$ las condiciones en los extremos:- Puesto que $u'_y(x,0)=0$, sabemos que $X(x)Y'(0)=0$ para cualquier $x$, por lo que $$Y'(0)=0$$
- Puesto que $u'_y(x,2)=0$, sabemos que $X(x)Y'(2)=0$ para cualquier $x$, por lo que $$Y'(2)=0$$
Paso 3
Encontrar todas las posibles soluciones del problema anterior. La ecuación es lineal homogénea de coeficientes constantes, luego para escribir su solución debemos encontrar las raíces de la ecuación característica: $$r^2=-\lambda$$ Las raíces serán reales diferentes, reales iguales o complejas conjugadas según sea el signo de $\lambda$, así que debemos separar tres casos:- Si $\lambda< 0$ (tomamos $\lambda=-\alpha^2$): ... encuentra las soluciones $Y(y)$ en este caso y pulsa en 'Ver'
Ver
Las raíces de la ecuación característica son $r=\pm \alpha$, reales y distintas, luego la solución general es $$Y(y)=Ae^{\alpha y}+Be^{-\alpha y}$$
por lo que $$Y'(y)=\alpha(Ae^{\alpha y}-Be^{-\alpha y})$$
Imponiendo que $Y'(0)=0$, tendremos que $A-B=0$ y con $Y'(2)=0$, puesto que $e^{2\alpha} \neq e^{-2\alpha}$, se concluye que $A=0$, y por tanto también $B=0$. Luego $Y\equiv 0$ es la única solución posible si $\lambda< 0$.
- Si $\lambda=0$, ...
La única posibilidad es que $Y\equiv 0$.
No hay solución del problema anterior.
Ninguna de las propuestas es correcta.
No es cierto, haz de nuevo las cuentas.
Sí hay soluciones.
En efecto, ninguna de las propuestas es correcta:
la solución general es $Y(y)=Ay+B$, luego $Y'(y)=A$, lo que significa que tomando $A=0$, ya se cumplen las dos condiciones de frontera, $Y'(0)=0$ y $Y'(2)=0$. Tanto la ecuación como las condiciones se cumplen sea cual sea $B$, luego todas las funciones $Y(y)$ múltiplos de $Y_0(y)=1$ son soluciones.
- Si $\lambda>0$ (tomamos $\lambda=\alpha^2$, con $\alpha>0$): las raíces son $r=\pm \alpha i$, escribe cuáles son las posibles $Y(y)$ en ese caso y pulsa en 'Ver'.
Ver
La solución general es $$Y(y)=A\cos \alpha y+B\,\mbox{sen} \alpha y$$
con lo cual
$$Y'(y)=\alpha(-A\,\mbox{sen} \alpha y+B \cos \alpha y)$$
De imponer que $Y'(0)=0$, tendremos que $B=0$; de imponer que $Y'(2)=0$, tendremos que $-A\,\mbox{sen} 2\alpha=0$, pues $\alpha\neq 0$. Puesto que nuestro objetivo son las soluciones no triviales, deberíamos poner $\mbox{sen} 2\alpha=0$, lo que conduce a que $\alpha=n\pi/2$ con $n$ cualquier número natural.
Esto quiere decir que el problema
$$Y''(y)+\lambda Y(y)=0 \hspace{.7cm} , \hspace{.7cm} Y'(0)=0 \hspace{.7cm} , \hspace{.7cm} Y'(2)=0$$
tiene solución no trivial para $\lambda_0=0$ y para todos los $\lambda_n=(n\pi/2)^2$, siendo las soluciones correspondientes los múltiplos de $$Y_0(y)=1 \hspace{.7cm}, \hspace{.7cm} Y_n(y)=\cos \frac{n\pi y}{2}\hspace{.4cm} \mbox{con}\ \ n \ \ \mbox{natural}$$
Paso 4
Resolver la solución correspondiente a $X(x)$: $$X''(x)-\lambda X(x)=0$$ teniendo en cuenta que hay una ecuación de éstas para cada $\lambda_n=(n\pi/2)^2$ con $n$ natural y para $\lambda_0=0$. A esta ecuación le añadimos la condición que se obtiene de $u(0,y)=0$. ¿Cuál es esa condición? Pulsa en 'Ver' cuando lo sepas.
Ver
$$u(0,y)=0 \hspace{.5cm}\Rightarrow \hspace{.5cm} X(0)Y(y)=0 \hspace{.5cm}\Rightarrow \hspace{.5cm} X(0)=0$$
Así pues los problemas para $X(x)$ son:
- para $\lambda_0$, $$X''_0=0 \hspace{.5cm} \mbox{con} \hspace{.3cm} X_0(0)=0$$ en este caso la solución general es $X_0(x)=Ax+B$, de donde $X_0(0)=B$; eso significa que
La única solución es $X_0(x)\equiv 0$
Ninguna de las dos propuestas es correcta.
Los posibles $X_0(x)$ son los múltiplos de $X(x)=x$
Eso no es correcto.
Sí hay una correcta.
En efecto, pues de $X_0(0)=B=0$ se deduce que cualquier función de la forma $Ax$ cumple la ecuación y la condición. Continuamos con los otros valores de $\lambda$:
- para cada $\lambda_n=(\frac{n\pi}{2})^2$, $$X''_n(x)-(\frac{n\pi}{2})^2 X_n(x)=0 \hspace{.5cm} \mbox{con} \hspace{.3cm} X_n(0)=0$$ La solución general en este caso es $$X_n(x)=A_ne^{n\pi x/2}+B_ne^{-n\pi x/2}$$ Impón la condición y encuentra las posibles funciones $X_n(x)$. Pulsa en 'Continuar' después.
$$X_n(0)=A_n+B_n=0 \hspace{.5cm}\Rightarrow \hspace{.5cm} B_n=-A_n \hspace{.5cm}\Rightarrow \hspace{.5cm} X_n(x)=A_n(e^{n\pi x/2}-e^{-n\pi x/2})$$
Paso 5
Utilizar la superposición de soluciones. Escribe tú la solución que se obtiene superponiendo todas las funciones $X(x)Y(y)$ obtenidas en los apartados anteriores y después pulsa en 'Ver'.
Ver
$$u(x,y)=A_0x+\sum_{n=1}^\infty A_n(e^{n\pi x/2}-e^{-n\pi x/2}) \cos \frac{n\pi y}{2}$$
Todavía faltan por determinar la constante $A_0$ y todas las $A_n$. Para ello recurriremos a la condición del problema de contorno que aún no hemos podido utilizar por no ser homogénea: $u(2,y)=y(2-y)$
Sustituyendo $x=2$, $$u(2,y)=2A_0+\sum_{n=1}^\infty A_n(e^{n\pi}-e^{-n\pi}) \cos \frac{n\pi y}{2}=y(2-y)$$ Esta igualdad es el desarrollo de la función $y(2-y)$ en serie de Fourier de cosenos en el intervalo $[0,2]$, lo que significa que $$2A_0=\int_0^2 y(2-y)\, dy \hspace{.5cm}, \hspace{.5cm} A_n(e^{n\pi x/2}-e^{-n\pi x/2})=\int_0^2y(2-y)\cos \frac{n\pi y}{2}\, dy$$ Podemos evaluar estas integrales a mano (por partes en el caso de la segunda) o en el ordenador, resultando $$A_0=\frac{1}{3} \hspace{.5cm}, \hspace{.5cm} A_n=\frac{-4(1+(-1)^n)}{n^2\pi^2\mbox{Sh}(n\pi)}$$ Teniendo en cuenta que $$A_n(e^{n\pi x/2}-e^{-n\pi x/2})=2A_n \mbox{Sh}\, \frac{n\pi x}{2}= \frac{-8(1+(-1)^n)}{n^2\pi^2\mbox{Sh}(n\pi)}\mbox{Sh}\, \frac{n\pi x}{2}$$ escribimos la solución final: $$u(x,y)=\frac{x}{3}-\frac{8}{\pi^2}\sum_{n=1}^\infty \frac{1+(-1)^n}{n^2\mbox{Sh}(n\pi)}\mbox{Sh}\, \frac{n\pi x}{2}\cos \frac{n\pi y}{2}$$ o bien, teniendo en cuenta que $1+(-1)^n=0$ si $n$ es impar y $1+(-1)^n=2$ si $n$ es par, $$u(x,y)=\frac{x}{3}-\frac{4}{\pi^2}\sum_{n=1}^\infty \frac{\mbox{Sh}(n\pi x)}{n^2\mbox{Sh}(2n\pi)}\cos (n\pi y)$$
Podemos dibujar la placa coloreada según esta función temperatura:
