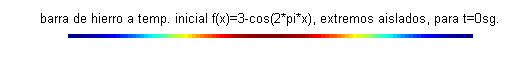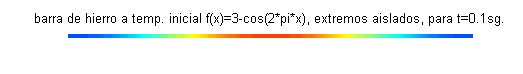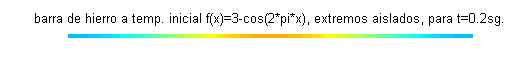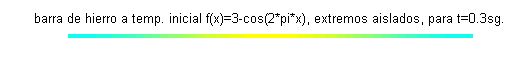Enunciado
El siguiente problema de contorno es un modelo para la distribución de temperatura (función $u(x,t)$) en una varilla delgada de longitud unidad, aislada tanto lateralmente como en sus extremos, si la temperatura inicial viene dada por $f(x)=3-\cos 2\pi x$: $$\left\{ \begin{array}{lll} u'_t=cu''_{xx} & ,\ 0<x <1 & , \ t>0\\ u'_x(0,t)=0=u'_x(1,t) & & , \ t>0 \\ u(x,0)=f(x)=3-\cos 2\pi x & ,\ 0\leq x \leq 1 & \\ \end{array}\right.$$ Hallar su solución formal aplicando el método de separación de variables.
Resolución
Paso 1
Buscar las funciones de la forma $u(x,t)=X(x)T(t)$ que verifiquen la ecuación y las condiciones para $x=0$ y para $x=1$ (condiciones en los extremos). Para ello encontramos $u'_t$ y $u''_{xx}$ y las igualamos. Hazlo tú y pulsa en 'Ver'.
Ver
$$u'_t=cu''_{xx} \hspace{.7cm} \Rightarrow \hspace{.7cm} X(x)T'(t)=cX''(x)T(t)
\hspace{.7cm} \Rightarrow \hspace{.7cm} \frac{T'(t)}{cT(t)}=\frac{X''(x)}{X(x)}$$
Puesto que esta última igualdad es cierta para cualquier $t>0$ y cualquier $x$ en el intervalo $(0,1)$ siendo estas dos variables independientes entre sí, la única manera que una función de $t$ (en este caso $\frac{T'}{cT}$) sea igual a una función de $x$, es que sea una constante. Llamamos $-\lambda$ a esa constante:
$$\frac{T'(t)}{cT(t)}=\frac{X''(x)}{X(x)}=-\lambda$$
o bien $$X''(x)+\lambda X(x)=0\hspace{.7cm} , \hspace{.7cm} T'(t)+\lambda c T(t)=0$$
Paso 2
Escribir para $X(x)$ las condiciones en los extremos:- Puesto que $u'_x(0,t)=0$, sabemos que $X'(0)T(t)=0$ para cualquier $t$, por lo que $$X'(0)=0$$
- Puesto que $u'_x(1,t)=0$, se tiene que $X'(1)T(t)=0$ para cualquier $t$, y por tanto $$X'(1)=0$$
Paso 3
Encontrar todas las posibles soluciones del problema anterior. La ecuación es lineal homogénea de coeficientes constantes, luego para escribir su solución debemos encontrar las raíces de la ecuación característica: $$r^2=-\lambda$$ Las raíces serán reales diferentes, reales iguales o complejas conjugadas según sea el signo de $\lambda$, así que debemos separar tres casos:- Si $\lambda< 0$ (tomamos $\lambda=-\alpha^2$): ... encuentra las soluciones $X(x)$ en este caso y pulsa en 'Ver'
Ver
Las raíces de la ecuación característica son $r=\pm \alpha$, reales y distintas, luego la solución general es $$X(x)=Ae^{\alpha x}+Be^{-\alpha x}$$
por lo que $$X'(x)=\alpha(Ae^{\alpha x}-Be^{-\alpha x})$$
Imponiendo que $X'(0)=0$, tendremos que $A-B=0$ y con $X'(1)=0$, puesto que $e^\alpha \neq e^{-\alpha}$, se concluye que $A=0=B$. Luego la única solución posible si $\lambda< 0$, es que $X\equiv 0$.
- Si $\lambda=0$, ...
La única posibilidad es que $X\equiv 0$.
No hay solución del problema anterior.
Ninguna de las propuestas es correcta.
No es cierto, haz de nuevo las cuentas.
Sí hay soluciones.
En efecto, ninguna de las propuestas es correcta:
la solución general es $X(x)=Ax+B$, luego $X'(x)=A$, lo que significa que tomando $A=0$, ya se cumplen las dos condiciones de frontera, $X'(0)=0$ y $X'(1)=0$. Tanto la ecuación como las condiciones se cumplen sea cual sea $B$, luego todas las funciones $X(x)$ múltiplos de $X_0(x)=1$ son soluciones.
- Si $\lambda>0$ (tomamos $\lambda=\alpha^2$, con $\alpha>0$): las raíces son $r=\pm \alpha i$, escribe cuáles son las posibles $X(x)$ en ese caso y pulsa en 'Ver'.
Ver
La solución general es $$X(x)=A\cos \alpha x+B\,\mbox{sen} \alpha x$$
con lo cual
$$X'(x)=\alpha(-A\,\mbox{sen} \alpha x+B \cos \alpha x)$$
De imponer que $X'(0)=0$, tendremos que $B=0$; de imponer que $X'(1)=0$, tendremos que $-A\,\mbox{sen} \alpha=0$, pues $\alpha\neq 0$. Puesto que nuestro objetivo son las soluciones no triviales, deberíamos poner $\mbox{sen} \alpha=0$, lo que conduce a que $\alpha=n\pi$ con $n$ cualquier número natural.
Esto quiere decir que el problema
$$X''(x)+\lambda X(x)=0 \hspace{.7cm} , \hspace{.7cm} X'(0)=0 \hspace{.7cm} , \hspace{.7cm} X'(1)=0$$
tiene solución no trivial para $\lambda_0=0$ y para todos los $\lambda_n=(n\pi)^2$, siendo las soluciones correspondientes los múltiplos de $$X_0(x)=1 \hspace{.7cm}, \hspace{.7cm} X_n(x)=\cos n\pi x\hspace{.4cm} \mbox{con}\ \ n \ \ \mbox{natural}$$
Paso 4
Resolver la solución correspondiente a $T(t)$: $$T'(t)+\lambda cT(t)=0$$ teniendo en cuenta que hay una ecuación de éstas para cada $\lambda_n=(n\pi)^2$ con $n$ natural y para $\lambda_0=0$.- para $\lambda_0$, la ecuación es $$T'_0=0$$ luego la solución general es $T_0(t)=C_0$.
- para cada $\lambda_n$, la ecuación es $$T'_n(t)+(n\pi)^2 cT_n(t)=0$$ cuya solución general es $$T_n(t)=C_ne^{-n^2\pi^2ct}$$
Paso 5
Utilizar la superposición de soluciones. Escribe tú la solución que se obtiene superponiendo todas las funciones $X(x)T(t)$ obtenidas en los apartados anteriores y después pulsa en 'Ver'.
Ver
$$u(x,t)=\sum_{n=0}^\infty X_n(x)T_n(t)=C_0+\sum_{n=1}^\infty C_n e^{-n^2\pi^2 c t} \cos n\pi x$$
Esta función cumple la ecuación y las condiciones en los extremos de la varilla. Únicamente resta aplicar la condición inicial:
$$u(x,0)=3-\cos 2\pi x \hspace{.7cm} \Rightarrow \hspace{.7cm} C_0+\sum_{n=1}^\infty C_n \cos n\pi x=3-\cos 2\pi x$$
de donde se deduce que $$C_0=3,\hspace{.5cm} C_2=-1,\hspace{.5cm} C_n=0\ \forall \ n\neq 0,\, 2$$
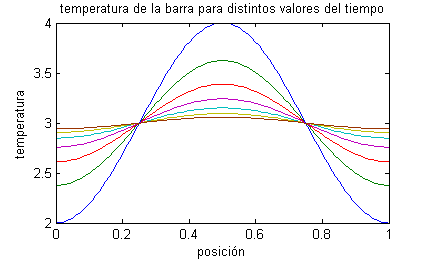
así que $$u(x,t)=3-e^{-4\pi^2 c t} \cos 2\pi x$$
La constante $c$ depende del material de la barra. Para el caso de una barra de hierro, tomamos $c=0.12$. A continuación se muestra una barra de hierro coloreada según la temperatura, para siete valores del tiempo entre $t=0$ y $t=0.6$: