Enunciado
El siguiente problema de contorno es un modelo para el desplazamiento vertical (función $u(x,t)$) de los puntos de una cuerda delgada elástica vibrando, estando los extremos de la curva (puntos correspondientes a $x=0$ y $x=1$) fijos a altura cero, si el desplazamiento inicial de la cuerda viene dado por $f(x)$ y la velocidad en cada punto es $g(x)$: $$\left\{ \begin{array}{lll} u''_{tt}=u''_{xx} & ,\ 0<x <1 & , \ t>0\\ u(0,t)=0=u(1,t) & & , \ t>0 \\ u(x,0)=f(x)=\frac{1}{2} \mbox{sen}\, 2\pi x-\frac{1}{5} \mbox{sen}\, 3\pi x & ,\ 0<x <1 & \\ u'_t(x,0)=g(x)=2\, \mbox{sen}\, 4\pi x & , \ 0\leq x \leq 1 & \end{array}\right.$$ Hallar su solución formal aplicando el método de separación de variables.
Resolución
Paso 1
Buscar las funciones de la forma $u(x,t)=X(x)T(t)$ que verifiquen la ecuación y las condiciones para $x=0$ y para $x=1$ (condiciones en los extremos). Para ello encontramos $u''_{tt}$ y $u''_{xx}$ y las igualamos. Hazlo tú y pulsa en 'Ver'.
Ver
$$u''_{tt}=u''_{xx} \hspace{.7cm} \Rightarrow \hspace{.7cm} T''(t)X(x)=X''(x)T(t)
\hspace{.7cm} \Rightarrow \hspace{.7cm} \frac{T''(t)}{T(t)}=\frac{X''(x)}{X(x)}$$
Puesto que esta última igualdad es cierta para cualquier $t>0$ y cualquier $x$ en el intervalo $(0,1)$ siendo estas dos variables independientes entre sí, la única manera que una función de $t$ (en este caso $\frac{T''}{T}$) sea igual a una función de $x$, es que sea una constante. Llamamos $-\lambda$ a esa constante:
$$\frac{T''(t)}{T(t)}=\frac{X''(x)}{X(x)}=-\lambda$$
o bien $$X''(x)+\lambda X(x)=0\hspace{.7cm} , \hspace{.7cm} T''(t)+\lambda T(t)=0$$
Paso 2
Escribir para $X(x)$ las condiciones en los extremos. Puesto que $u(0,t)=0$,...
$T(t)=0$ para cualquier $t$
Ninguna de las dos propuestas es correcta.
$X(0)=0$
Eso puede ser cierto, pero conduce a la solución trivial, $u=0$; así que no nos sirve.
Sí hay una correcta.
En efecto, eso se deduce de que $u(0,t)=0=X(0)T(t)=0$. Lo mismo ocurre con la condición en el otro extremo, $x=1$, con lo cual, de las posibles funciones $X(x)$ sabemos que
$$X''(x)+\lambda X(x)=0\hspace{.7cm} , \hspace{.7cm} X(0)=0 \hspace{.7cm} , \hspace{.7cm} X(1)=0$$
Paso 3
Encontrar todas las posibles soluciones del problema anterior. La ecuación es lineal homogénea de coeficientes constantes, luego para escribir su solución debemos encontrar las raíces de la ecuación característica: $$r^2=-\lambda$$
las raíces son $r_1=\sqrt{\lambda}i$ y $r_2=-\sqrt{\lambda}i$
las raíces son $r_1=\sqrt{\lambda}$ y $r_2=-\sqrt{\lambda}$
Ninguna de las propuestas es correcta.
Eso sería correcto únicamente en el caso en que $\lambda$ fuera positivo.
No es correcto.
En efecto, ninguna es correcta. Las raíces de la ecuación características tendrán distintas expresiones según sea el signo de $\lambda$:
- Si $\lambda< 0$ (tomamos $\lambda=-\alpha^2$): las raíces son $r=\pm \alpha$, reales y distintas, luego la solución general es $$X(x)=Ae^{\alpha x}+Be^{-\alpha x}$$ Imponiendo que $X(0)=0$, tendremos que $A+B=0$ y con $X(1)=0$, puesto que $e^\alpha \neq e^{-\alpha}$, se concluye que $A=0=B$. Luego la única solución posible si $\lambda< 0$, es que $X\equiv 0$.
- Si $\lambda=0$, encuentra la solución general y aplica las condiciones en los extremos; pulsa en 'Continuar' cuando lo tengas.
Si $\lambda=0$, la ecuación característica tiene al cero como raíz doble, así que la solución general es
$$X(x)=Ax+B$$
debido a que $X(0)=0$, tendremos que $B=0$ y debido a que $X(1)=0$, resulta $A=0$. Así que la única solución posibe en este caso vuelve a ser $X\equiv 0$.
- Si $\lambda>0$ (tomamos $\lambda=\alpha^2$, con $\alpha>0$): las raíces son $r=\pm \alpha i$, escribe cuáles son las posibles $X(x)$ en ese caso y pulsa en 'Ver'.
Ver
La solución general es $$X(x)=A\cos \alpha x+B\,\mbox{sen} \alpha x$$
De imponer que $X(0)=0$, tendremos que $A=0$; de imponer que $X(1)=0$, tendremos que $B\,\mbox{sen} \alpha=0$. Puesto que nuestro objetivo son las soluciones no triviales, deberíamos poner $\mbox{sen} \alpha=0$, lo que conduce a
$\alpha=0$
$\alpha=n\pi$, con $n$ cualquier número entero
$\alpha=n\pi$, con $n$ cualquier número natural
Es cierto que el seno de cero es cero, pero hay más opciones
Es cierto que $\mbox{sen} n\pi=0$ para cualquier $n$ entero, pero estamos trabajando en el supuesto de que $\alpha>0$
En efecto, por ser $\alpha>0$, la condición $\mbox{sen} \alpha=0$ conduce a que $\alpha=n\pi$, con $n$ cualquier número natural. Es decir, para cada número natural existe un valor de $\lambda$ para el cual el problema
$$X''(x)+\lambda X(x)=0\hspace{.7cm} , \hspace{.7cm} X(0)=0 \hspace{.7cm} , \hspace{.7cm} X(1)=0$$
tiene solución no nula. El valor correspondiente al natural $n$ es $\lambda_n=(n\pi)^2$ y las soluciones al problema
$$X''(x)+\lambda_n X(x)=0\hspace{.7cm} , \hspace{.7cm} X(0)=0 \hspace{.7cm} , \hspace{.7cm} X(1)=0$$
son los multiplos de la función $$X_n(x)=\mbox{sen}\, n\pi x$$
Paso 4
Resolver la solución correspondiente a $T(t)$: $$T''(t)+\lambda T(t)=0$$ teniendo en cuenta que hay una ecuación de éstas para cada $n$ natural, aunque todas respondan a la misma forma: $$T''_n(t)+(n\pi)^2\lambda T_n(t)=0$$ Encuentra la solución general de esta ecuación y pulsa en 'Ver'
Ver
Las raíces de la ecuación característica son $r=\pm(n\pi) i$, luego las soluciones para $T_n(t)$ son
$$T_n(t)=A_n \cos n\pi t+B_n\, \mbox{sen}\, n\pi t$$
Paso 5
Utilizar la superposición de soluciones. Esto es, generar una solución del problema $$\left\{ \begin{array}{lll} u''_{tt}=u''_{xx} & ,\ 0<x <1 & , \ t>0\\ u(0,t)=0=u(1,t) & & , \ t>0 \\ u(x,0)=f(x)=\frac{1}{2} \mbox{sen}\, 2\pi x-\frac{1}{5} \mbox{sen}\, 3\pi x & ,\ 0<x <1 & \\ u'_t(x,0)=g(x)=2\, \mbox{sen}\, 4\pi x & , \ 0\leq x \leq 1 & \end{array}\right.$$ como suma infinita de todas las $u_n(x,t)=X_n(x)T_n(t)$ obtenidas en los pasos anteriores: $$u(x,t)=\sum_{n=1}^\infty X_n(x)T_n(t)=\sum_{n=1}^\infty (A_n \cos n\pi t+B_n\, \mbox{sen}\, n\pi t)\, \mbox{sen}\, n\pi x $$ Puesto que la ecuación es lineal y cada uno de los sumandos $X_n(x)T_n(t)$ es solución, la suma también es solución de la ecuación. Y además, $$u(0,t)=\sum_{n=1}^\infty X_n(0)T_n(t)=0 \hspace{.7cm} \mbox{y} \hspace{.7cm} u(1,t)=\sum_{n=1}^\infty X_n(1)T_n(t)=0$$ ya que $X_n(0)=0$ y $X_n(1)=0$ para cualquier $n$. Así pues, las únicas condiciones que han de imponerse a esta función $u(x,t)$ son las dos iniciales (las correspondientes a $t=0$). Aplica la condición para $u(x,0)$ y pulsa en 'Ver'.
Ver
$$u(x,0)=\sum_{n=1}^\infty A_n \mbox{sen}\, n\pi x = \frac{1}{2} \mbox{sen}\, 2\pi x-\frac{1}{5} \mbox{sen}\, 3\pi x$$
lo que significa que
$$A_2=\frac{1}{2} \hspace{.7cm} , \hspace{.7cm} A_3=\frac{-1}{5} \hspace{.7cm} , \hspace{.7cm} A_n=0 \ \forall \ n\neq 2,\, 3$$
De igual manera procedemos con la condición para $u'_t(x,0)$. Pulsa en continuar cuando lo tengas.
$$u'_t(x,0)=\sum_{n=1}^\infty n\pi B_n \mbox{sen}\, n\pi x = 2\, \mbox{sen}\, 4\pi x$$
de donde
$$B_4=\frac{1}{2\pi} \hspace{.7cm} , \hspace{.7cm} B_n=0\ \forall\ n\neq 4$$
Con todo esto, la solución final es
$$u(x,t)=\frac{1}{2} \cos 2\pi t\, \mbox{sen}\, 2\pi x-\frac{1}{5} \cos 3\pi t\,\mbox{sen}\, 3\pi x+\frac{1}{2\pi} \, \mbox{sen}\, 4\pi t\, \mbox{sen}\, 4\pi x$$
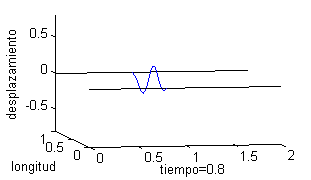
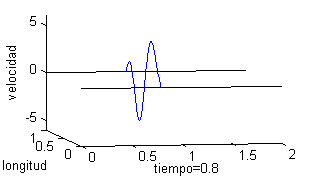
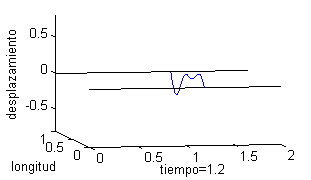
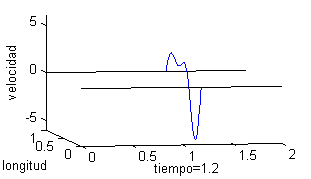
Podemos representar esta solución como una superficie, pero puede ser más ilustrativo trazar la gráfica del desplazamiento de un punto de la cuerda respecto del tiempo o bien dibujar la cuerda para distintos valores del tiempo. Esto es lo que recogemos a continuación, tomando seis valores del tiempo, desde $t=0$ a $t=2$; en la columna de la izquierda vemos la cuerda para esos valores del tiempo y en la derecha las gráficas de la velocidad:
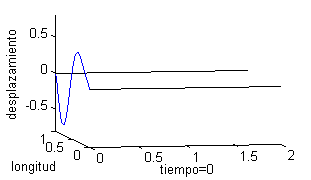 |
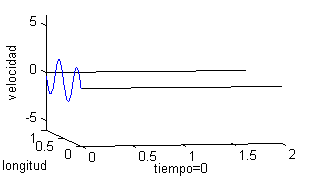 |
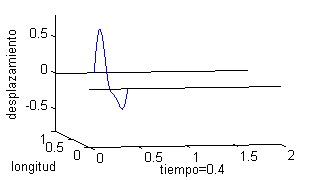 |
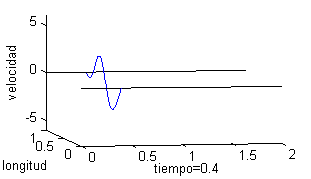 |
 |
 |
 |
 |
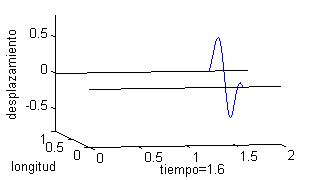 |
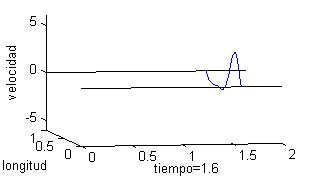 |
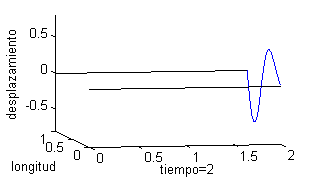 |
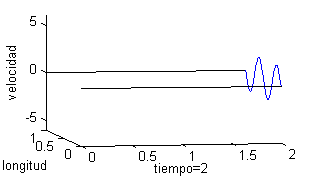 |