Enunciado
Comprueba que si una función $z(x,y)$ verifica la ecuación $$(z'_x)^2+(z'_y)^2=C$$ y realizamos un giro de ángulo $\alpha$ en las variables $x$ e $y$ $$x=(\cos \alpha) u-(\mbox{sen}\, \alpha) v \hspace{.7cm} , \hspace{.7cm} y=(\mbox{sen}\, \alpha) u+(\cos \alpha) v$$ entonces la función $z(u,v)$ verifica la misma ecuación $$(z'_u)^2+(z'_v)^2=C$$
Resolución
Para simplificar la notación llamamos
$$A=\cos \alpha \hspace{.7cm}, \hspace{.7cm} B=\mbox{sen}\, \alpha$$
de manera que el cambio de variable es
$$x=A u-B v \hspace{.7cm} , \hspace{.7cm}
y=B u+A v$$
Paso 1
Expresar las derivadas parciales primeras de $z$ respecto de $u$ y respecto de $v$ en función de las derivadas respecto de $x$ y respecto de $y$. El árbol de dependencia es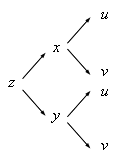
Ver
$$\left.\begin{array}{l} x'_u=A \\ y'_u=B \\ x'_v=-B \\ y'_v=A \end{array}\right\} \hspace{.4cm} \Rightarrow \hspace{.4cm}
\left\{\begin{array}{l} z'_u=Az'_x+Bz'_y \\ z'_v=-Bz'_x+Az'_y \end{array}\right.$$
Paso 2
Sustituir estas expresiones en $(z'_u)^2+(z'_v)^2$; hazlo tú y pulsa en 'Ver'.
Ver
$$(z'_u)^2+(z'_v)^2=A^2(z'_x)^2+B^2(z'_y)^2+2ABz'_xz'_y+B^2(z'_x)^2+A^2(z'_y)^2-2ABz'_xz'_y=(A^2+B^2)((z'_x)^2+(z'_y)^2)$$
Pero sabemos que $A^2+B^2=1$ puesto que $A=\cos \alpha$ y $B=\mbox{sen}\, \alpha$. Por tanto queda demostrado que $$(z'_u)^2+(z'_v)^2=(z'_x)^2+(z'_y)^2$$