Enunciado
- Encuentra la relación existente entre $z''_{xx}$ y $z''_{yy}$ para $$z(x,y)=f(xy)+\sqrt{xy}g\left(\frac{y}{x}\right)$$
- Escribe dos soluciones diferentes de la e.d.p. encontrada en el apartado anterior y represéntalas en un dominio rectangular apropiado.
Resolución del primer apartado
Paso 1
Derivar $z(x,y)$ una vez respecto de $x$:
$$z'_x(x,y)=yf'_x(xy)+\frac{1}{2}\sqrt{\frac{y}{x}}g\left(\frac{y}{x}\right)+\sqrt{xy}\left(-\frac{y}{x^2}\right)g'_x\left(\frac{y}{x}\right)$$
$$z'_x(x,y)=yf'_x(xy)+\frac{1}{2}\sqrt{\frac{y}{x}}g\left(\frac{y}{x}\right)+\sqrt{xy}g'_x\left(\frac{y}{x}\right)$$
Ninguna de las opciones presentadas es correcta.
Eso está muy mal derivado, pues $f$ y $g$ son funciones de una variable, no se hacen sus parciales.
Eso está muy mal derivado, pues $f$ y $g$ son funciones de una variable, no se hacen sus parciales, y además en el último sumando faltaría la derivada de $\frac{y}{x}$.
En efecto, ninguna de las propuestas es correcta. Las funciones $f$ y $g$ lo son de una sóla variable, no las podemos derivar parcialmente respecto de $x$ ni respecto de $y$:
$$z'_x(x,y)=yf'(xy)+\frac{1}{2}\sqrt{\frac{y}{x}}g\left(\frac{y}{x}\right)+\sqrt{xy}\left(-\frac{y}{x^2}\right)g'\left(\frac{y}{x}\right)$$
o bien
$$z'_x(x,y)=yf'(xy)+\frac{1}{2}\sqrt{\frac{y}{x}}g\left(\frac{y}{x}\right)-\frac{y}{x}\sqrt{\frac{y}{x}}g'\left(\frac{y}{x}\right)$$
Paso 2
Derivar de nuevo respecto de $x$. Hazlo tú y pulsa en 'Ver' cuando termines.
Ver
$$z''_{xx}(x,y)=y^2f''(xy)-\frac{1}{4x}\sqrt{\frac{y}{x}}g\left(\frac{y}{x}\right)+\frac{1}{2}\sqrt{\frac{y}{x}}\left(-\frac{y}{x^2}\right)g'\left(\frac{y}{x}\right)+\frac{3y}{2x^2}\sqrt{\frac{y}{x}}g'\left(\frac{y}{x}\right)-\frac{y}{x}\sqrt{\frac{y}{x}}\left(-\frac{y}{x^2}\right)g''\left(\frac{y}{x}\right)$$
o bien
$$z''_{xx}(x,y)=y^2f''(xy)-\frac{1}{4x}\sqrt{\frac{y}{x}}g\left(\frac{y}{x}\right)+\frac{y}{x^2}\sqrt{\frac{y}{x}}g'\left(\frac{y}{x}\right)+\frac{y^2}{x^3}\sqrt{\frac{y}{x}}g''\left(\frac{y}{x}\right)$$
Paso 3
Derivar $z(x,y)=f(xy)+\sqrt{xy}g\left(\frac{y}{x}\right)$ una vez respecto de $y$:
$$z'_y(x,y)=xf'(xy)+\frac{1}{2}\sqrt{\frac{x}{y}}g\left(\frac{y}{x}\right)+\sqrt{xy}g'\left(\frac{y}{x}\right)$$
$$z'_y(x,y)=xf'(xy)+\frac{1}{2}\sqrt{\frac{x}{y}}g'\left(\frac{y}{x}\right)$$
Ninguna de las propuestas es correcta.
$$z'_y(x,y)=xf'(xy)+\frac{1}{2}\sqrt{\frac{x}{y}}g\left(\frac{y}{x}\right)+\sqrt{xy}\frac{1}{x}g'\left(\frac{y}{x}\right)$$
No es correcto porque está mal el último sumando.
Muy mal derivado.
Sí hay una correcta.
En efecto, ésa es la derivada primera de $z$ respecto de $y$.
Paso 4
Derivar de nuevo respecto de $y$, para hallar $z''_{yy}$. Hazlo tú y pulsa en 'Ver' cuando termines.
Ver
$$z''_{yy}(x,y)=x^2f''(xy)-\frac{1}{4y}\sqrt{\frac{x}{y}}g\left(\frac{y}{x}\right)+\frac{1}{2x}\sqrt{\frac{x}{y}}g'\left(\frac{y}{x}\right)+\frac{1}{2\sqrt{xy}}g'\left(\frac{y}{x}\right)+\frac{1}{x}\sqrt{\frac{y}{x}}g''\left(\frac{y}{x}\right)$$
o bien
$$z''_{yy}(x,y)=x^2f''(xy)-\frac{1}{4y}\sqrt{\frac{x}{y}}g\left(\frac{y}{x}\right)+\frac{1}{\sqrt{xy}}g'\left(\frac{y}{x}\right)+\frac{1}{x}\sqrt{\frac{y}{x}}g''\left(\frac{y}{x}\right)$$
Observamos que tanto $z''_{xx}$ como $z''_{yy}$ están compuestos por cuatro sumandos, uno con la función $f''(xy)$, otro con $g\left(\frac{y}{x}\right)$, otro con $g'\left(\frac{y}{x}\right)$ y el último con $g''\left(\frac{y}{x}\right)$; recogemos en la siguiente tabla los coeficientes de estas funciones en $z''_{xx}$ y $z''_{yy}$:
Si multiplicamos los coeficientes en $z''_{xx}$ por $x^2$ y los de $z''_{yy}$ por $y^2$, tendremos
esto es, $z(x,y)$ verifica que $$x^2z''_{xx}=y^2z''_{yy}$$
| los coeficientes de | $$f''(xy)$$ | $$g\left(\frac{y}{x}\right)$$ | $$g'\left(\frac{y}{x}\right)$$ | $$g''\left(\frac{y}{x}\right)$$ |
| en $z''_{xx}$ son | $$y^2$$ | $$-\frac{1}{4x}\sqrt{\frac{y}{x}}$$ | $$\frac{y}{x^2}\sqrt{\frac{y}{x}}$$ | $$\frac{y^2}{x^3}\sqrt{\frac{y}{x}}$$ |
| en $z''_{yy}$ son | $$x^2$$ | $$-\frac{1}{4y}\sqrt{\frac{x}{y}}$$ | $$\frac{1}{\sqrt{xy}}$$ | $$\frac{1}{x}\sqrt{\frac{y}{x}}$$ |
| los coeficientes de | $$f''(xy)$$ | $$g\left(\frac{y}{x}\right)$$ | $$g'\left(\frac{y}{x}\right)$$ | $$g''\left(\frac{y}{x}\right)$$ |
| en $x^2z''_{xx}$ son | $$x^2y^2$$ | $$-\frac{x}{4}\sqrt{\frac{y}{x}}$$ | $$y\sqrt{\frac{y}{x}}$$ | $$\frac{y^2}{x}\sqrt{\frac{y}{x}}$$ |
| en $y^2z''_{yy}$ son | $$y^2x^2$$ | $$-\frac{y}{4}\sqrt{\frac{x}{y}}$$ | $$y^2\frac{1}{\sqrt{xy}}$$ | $$\frac{y^2}{x}\sqrt{\frac{y}{x}}$$ |
Resolución del segundo apartado
Construiremos dos ejemplos de soluciones pertenecientes a la familia $z(x,y)=f(xy)+\sqrt{xy}g\left(\frac{y}{x}\right)$.Primera solución
Tomamos $f(t)=\mbox{sen}\, 4t^2$, $g(t)=e^t$; la función $z(x,y)$ resultante es ... escríbela tú y pulsa en 'Ver'.
Ver
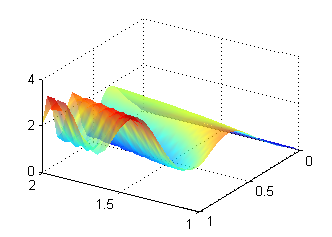
$$z(x,y)=\mbox{sen}(4x^2y^2)+\sqrt{xy}e^{\frac{y}{x}}$$
La representaremos en el rectángulo $[1,2]x[0,1]$, escribiendo
[X,Y]=meshgrid(1:.05:2,0:.05:1); Z=sin(4*X.^2.*Y.^2)+sqrt(X.*Y).*exp(Y./X); surf(X,Y,Z) shading interp alpha(.7)de cuya ejecución se obtiene
Segunda solución
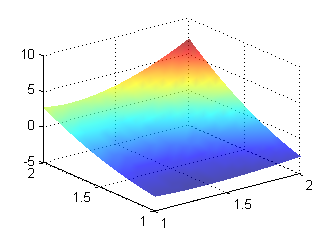
Tomamos $f(t)=t^2-2t-3$, $g(t)=t^2$; la función $z(x,y)$ resultante es $$z(x,y)=x^2y^2-2xy-3+\sqrt{xy}\left(\frac{y}{x}\right)^2$$ Escribe las líneas de código con las que representas esta función en el rectángulo $[1,2]x[1,2]$ y pulsa en 'Ver'.
Ver
[X,Y]=meshgrid(1:.05:2); Z=X.^2.*Y.^2-2*X.*Y-3+Y.^(5/2).*X.^(-3/2); surf(X,Y,Z) shading interp alpha(.7)genera la figura