Índice de tema

 

Enunciado

  1. Comprueba que cualquier función $u(x,y)$ de la forma $$u(x,y)=f(x+g(y))$$ es solución de la e.d.p. $u''_{xx}u'_y=u''_{xy}u'_x$. (Se supone que las funciones $f$ y $g$ son suficientemente derivables)
  2. Escribe cuatro soluciones diferentes de $u''_{xx}u'_y=u''_{xy}u'_x$ y represéntalas en un dominio rectangular apropiado.

Resolución del primer apartado

Paso 1

Derivar $u(x,y)$ una vez respecto de $y$:
$$u'_y(x,y)=f'_y(x+g(y))$$
$$u'_y(x,y)=f'_y(x+g(y))g'(y)$$
$$u'_y(x,y)=f'(x+g(y))$$
$$u'_y(x,y)=f'(x+g(y))g'(y)$$
Eso está muy mal derivado, pues $f$ es una función de una variable y $x+g(y)$ es función de $y$.
Eso está muy mal derivado, pues $f$ es una función de una variable, no existe por tanto su derivada parcial respecto de $y$.
No, pues $x+g(y)$ es función de $y$.
En efecto, esa es la primera derivada parcial de $u(x,y)$ respecto de $y$.

Paso 2

Derivar $u(x,y)$ una vez respecto de $x$:
$$u'_x(x,y)=f'_x(x+g(y))(1+g'(y))$$
$$u'_x(x,y)=f'(x+g(y))(1+g'(y))$$
$$u'_x(x,y)=f'(x+g(y))$$
Muy mal derivado, pues $f$ es una función de una variable, no existe por tanto su derivada parcial respecto de $x$ y $g(y)$ no depende de $x$
Muy mal derivado, pues $g(y)$ no depende de $x$
En efecto es la primera derivada parcial de $u(x,y)$ respecto de $x$.

Paso 3

Hallar $u''_{xx}(x,y)$. Hazlo tú y pulsa en 'Ver' cuando lo tengas.
Ver
$$u''_{xx}=f''(x+g(y))$$

Paso 4

Hallar $u''_{xy}(x,y)$. Hazlo tú y pulsa en 'Continuar' cuando lo tengas.
$$u''_{xy}=f''(x+g(y))g'(y)$$ Podemos ahora hacer el producto $$u''_{xx}u'_y=f''(x+g(y))f'(x+g(y))g'(y)$$ y el producto $$u''_{xy}u'_x=f''(x+g(y))g'(y)f'(x+g(y))$$ comprobando que efectivamente son iguales para cualesquiera funciones $f$ y $g$.

Resolución del segundo apartado

Se expondrán aquí cuatro ejemplos de soluciones, todas ellas por tanto pertenecientes a la familia $u(x,y)=f(x+g(y))$.

Primera solución

Tomamos $f(t)=\mbox{sen}\, t$, $g(t)=t^2$; la función $u(x,y)$ resultante es ... escríbela tú y pulsa en 'Ver'.
Ver
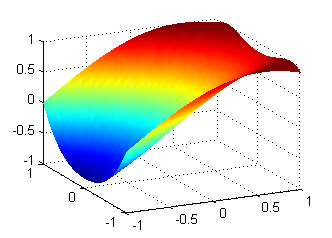
$$u(x,y)=\mbox{sen}(x+y^2)$$ La representaremos en el rectángulo $[-1,1]x[-1,1]$, escribiendo 
[X,Y]=meshgrid(-1:.05:1);
Z=sin(X+Y.^2);
surf(X,Y,Z)
shading interp
de cuya ejecución se obtiene

Gráfica

Segunda solución

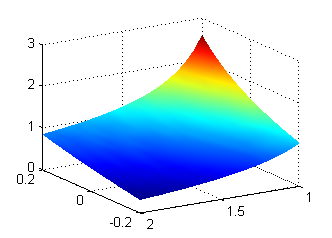
Tomamos $f(t)=\mbox{tg}\, t$, $g(t)=1/t$; la función $u(x,y)$ resultante es $$u(x,y)=\mbox{tg}\left(x+\frac{1}{y}\right)$$ Escribe las líneas de código con las que representas esta función en el rectángulo $[-2,2]x[1,2]$ y pulsa en 'Ver'.
Ver 
[X,Y]=meshgrid(-.2:.05:.2,1:0.05:2);
Z=tan(X+1./Y);
surf(X,Y,Z)
shading interp
genera la figura

Gráfica

Tercera solución

Tomamos $f(t)=t^2$, $g(t)=\mbox{sen}\, t$; la función $u(x,y)$ correspondiente es ... escríbela tú y pulsa en 'Ver'.
Ver
$$u(x,y)=(x+\mbox{sen}\, y)^2$$ Escribe las líneas de código con las que representas esta función en el rectángulo $[-.5,.5]x[-\pi,\pi]$ y pulsa en 'Continuar'.
La figura

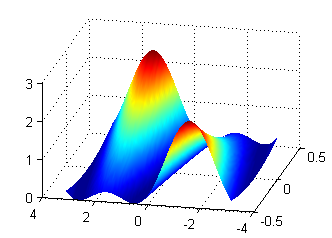
Gráfica

se genera con las líneas 
[X,Y]=meshgrid(-.5:.05:.5,-pi:.05:pi);
Z=(X+sin(Y)).^2;
surf(X,Y,Z)
shading interp

Cuarta solución

Por último, tomamos $f(t)=\frac{1}{t^2+1}$, $g(t)=t^4$; la función $u(x,y)$ correspondiente es ... escríbela tú y pulsa en 'Ver'.
Ver
$$u(x,y)=\frac{1}{(x+y^4)^2+1}$$ Escribe las líneas de código con las que representas esta función en el rectángulo $[-1,1]x[-1,1]$ y pulsa en 'Continuar'.
Para generar la figura

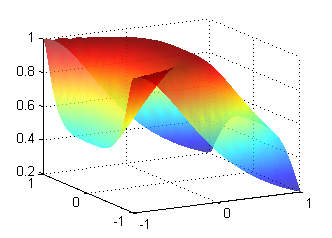
Gráfica

ejecutamos las líneas 
[X,Y]=meshgrid(-1:.05:1);
Z=1./((X+Y.^4).^2+1);
surf(X,Y,Z)
shading interp
alpha(.7)