Ejercicios preliminares e instantáneos. Ecuaciones en derivadas parciales (método de líneas)

Ejercicio 1

  1. Completa la siguiente tabla, en la que se generan nueve funciones diferentes, combinando tres funciones $f(t)$ de una variable con tres funciones de dos variables $t=v(x,y)$. Por ejemplo, la función de la celda 1-1 es $u(x,y)=\cos (xy)$.

    $t=xy$ $t=x^2+y$ $t=x/y$
    $f(t)= \cos t$
    $f(t)=t^3$
    $f(t)=t+\log t$

  2. Escribe las derivadas parciales primeras respecto de $x$ y las parciales primeras respecto de $y$ de las nueve funciones resultantes.
Pista
Solución
Si $t=v(x,y)$ la composición $f(v(x,y))$ es una función de dos variables, de manera que podemos hablar de sus derivadas parciales respecto de $x$ y de $y$. Por ejemplo, si $v(x,y)=x^2+y$ y $f(t)=t^2$, la composición es $u(x,y)=(x^2+y)^2$ y sus derivadas parciales serán $$u'_x(x,y)=f'(v(x,y))v'_x(x,y)=4(x^2+y)x$$ y $$u'_y(x,y)=f'(v(x,y))v'_y(x,y)=2(x^2+y)$$
  1. Las funciones $u(x,y)$ que se forman son:

    $t=xy$ $t=x^2+y$ $t=x/y$
    $f(t)= \cos t$ $u(x,y)=\cos(xy)$ $u(x,y)=\cos(x^2+y)$ $u(x,y)=\cos(x/y)$
    $f(t)=t^3$ $u(x,y)=x^3y^3$ $u(x,y)=(x^2+y)^3$ $u(x,y)=x^3/y^3$
    $f(t)=t+\log t$ $u(x,y)=xy+\log(xy)$ $u(x,y)=x^2+y+\log(x^2+y)$ $u(x,y)=\frac{x}{y}+\log\frac{x}{y}$

  2. Las derivadas parciales primeras de estas funciones son:

    $u(x,y)=$ $u'_x(x,y)=$ $u'_y(x,y)=$
    $\cos(xy)$ $-y\,\mbox{sen}(xy)$ $-x\, \mbox{sen}(xy)$
    $\cos(x^2+y)$ $-2x\mbox{sen}(x^2+y)$ $-\mbox{sen}(x^2+y)$
    $\cos(\frac{x}{y})$ $\frac{-1}{y}\,\mbox{sen}(\frac{x}{y})$ $\frac{x}{y^2}\,\mbox{sen}(\frac{x}{y})$
    $x^3y^3$ $3x^2y^3$ $3x^3y^2$
    $(x^2+y)^3$ $6x(x^2+y)^2$ $3(x^2+y)^2$
    $\frac{x^3}{y^3}$ $3\frac{x^2}{y^3}$ $\frac{-3x^3}{y^4}$
    $xy+\log(xy)$ $y+\frac{1}{x}$ $x+\frac{1}{y}$
    $x^2+y+\log(x^2+y)$ $2x+\frac{2x}{x^2+y}$ $1+\frac{1}{x^2+y}$
    $\frac{x}{y}+\log\frac{x}{y}$ $\frac{1}{y}+\frac{1}{x}$ $\frac{-x}{y^2}-\frac{1}{y}$

Ejercicio 2

  1. Escribe la expresión de la derivada parcial de $u(x,y)=f(v(x,y))$ respecto de $x$.
  2. Escribe la expresión de la derivada parcial de $u(x,y)=f(v(x,y))$ respecto de $y$.
Solución
$$u(x,y)=f(v(x,y))\hspace{.6cm} \Rightarrow \hspace{.6cm} \left\{ \begin{array}{l} u'_x(x,y)=f'(v(x,y))v'_x(x,y) \\ u'_y(x,y)=f'(v(x,y))v'_y(x,y) \end{array} \right.$$

Ejercicio 3

  1. Comprueba por derivación y sustitución que las funciones $$u(x,y)=xy+x^2y^2 \hspace{.3cm},\hspace{.7cm} u(x,y)=\mbox{sen}(xy)\hspace{.3cm},\hspace{.7cm} u(x,y)=\frac{1}{xy}+e^{xy}$$ son soluciones de la ecuación $xu'_x=yu'_y$.
  2. Comprueba que, de hecho, es solución de esa ecuación cualquier función de la forma $u(x,y)=f(xy)$, siendo $f(t)$ una función derivable cualquiera.
Solución
  1. En el primer caso, $$u(x,y)=xy+x^2y^2 \hspace{.7cm} \Rightarrow \hspace{.7cm} u'_x(x,y)=y+2xy^2 \hspace{.4cm} \mbox{y} \hspace{.4cm} u'_y(x,y)=x+2x^2y $$ luego $xu'_x=yu'_y$. Lo mismo ocurre en el segundo caso: $$u(x,y)=\mbox{sen}(xy) \hspace{.7cm} \Rightarrow \hspace{.7cm} u'_x(x,y)=y\cos (xy) \hspace{.4cm} \mbox{y} \hspace{.4cm} u'_y(x,y)=x\cos (xy) $$ y en el tercero: $$u(x,y)=\frac{1}{xy}+e^{xy} \hspace{.7cm} \Rightarrow \hspace{.7cm} u'_x(x,y)=\frac{-1}{x^2y}+ye^{xy} \hspace{.4cm} \mbox{y} \hspace{.4cm} u'_y(x,y)=\frac{-1}{xy^2}+xe^{xy} $$
  2. Si $u=f(x,y)$, las primeras derivadas parciales son $u'_x=yf'(xy)$ y $u'_y=xf'(xy)$ luego en efecto se cumple que $xu'_x=yu'_y$

Ejercicio 4

Escribe las derivadas parciales primeras y segundas de $u(x,y)$ en función de las parciales de $v(x,y)$ si las funciones $v(x,y)$ y $u(x,y)$ se relacionan por $u(x,y)=x^2v(x,y)$.
Solución
  • $u'_x=2xv+x^2v'_x$
  • $u'_y=x^2v'_y$
  • $u''_{xx}=2v+4xv'_x+x^2v''_{xx}$
  • $u''_{yy}=x^2v''_{yy}$
  • $u''_{xy}=2xv'_y+x^2v''_{xy}$
  • $u''_{yx}=2xv'_y+x^2v''_{yx}$

Ejercicio 5

Encuentra la ecuación que verifica $v(x,y)$ sabiendo que $u(x,y)=x^2v(x,y)$ y que $u(x,y)$ es solución de la ecuación $u''_{xx}=u'_y$.
Pista
Solución
Empieza escribiendo $u''_{xx}$ y $u'_y$ en función de las parciales de $v$ y después iguálalas.
Puesto que $$u''_{xx}=2v+4xv'_x+x^2v''_{xx}$$ y $$u'_y=x^2v'_y$$ la función $v(x,y)$ verifica la ecuación $$2v+4xv'_x+x^2v''_{xx}=x^2v'_y$$

Ejercicio 6

  1. Comprueba que la función $$u(x,t)=e^{-4\pi^2t}\mbox{sen}\, 2\pi x-2e^{-9\pi^2t}\mbox{sen}\, 3\pi x$$ es solución del problema $$\left\{\begin{array}{lll} \frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial x^2}, & 0<x<1, & t>0\\ u(0,t)=0, & & t>0 \\ u(1,t)=0, & & t>0 \\ u(x,0)=\mbox{sen}\, 2\pi x-2\mbox{sen}\, 3\pi x, & 0\leq x \leq 1 & \end{array}\right.$$
  2. Si llamamos $u_k(t)=u(x_k,t)$, escribe las cinco funciones $u_k(t)$, para $k=0,\,\ldots,\, 4$ siendo $x_k=k/4$.
Solución
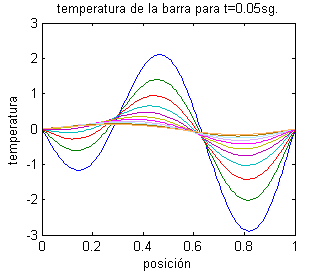
  1. Derivando $u(x,t)$ una vez respecto de $t$: $$u'_t=-4\pi^2e^{-4\pi^2t}\mbox{sen}\, 2\pi x+18\pi^2e^{-9\pi^2t}\mbox{sen}\, 3\pi x$$ que es la misma expresión que se obtiene derivando $u(x,t)$ dos veces respecto de $x$. Además $u(0,t)=0$, $u(1,t)=0$ y $u(x,0)=\mbox{sen}\, 2\pi x-2\mbox{sen}\, 3\pi x$. Este problema constituye un modelo para la temperatura (función $u(x,t)$) de los puntos de una varilla aislada de longitud 1, cuyos extremos se mantienen a 0 grados y la temperatura inicial en cada punto viene dada por $f(x)=\mbox{sen}\, 2\pi x-2\mbox{sen}\, 3\pi x$.A continuación se muestra la varilla coloreada según la función $u(x,t)$, para distintos valores del tiempo:

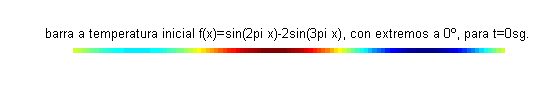
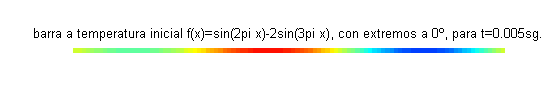
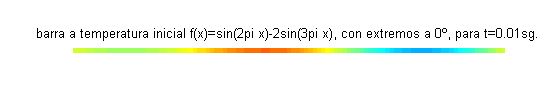
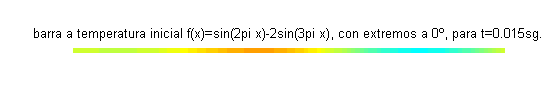
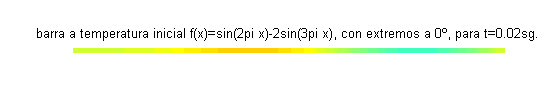
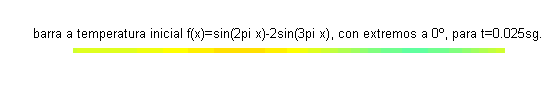
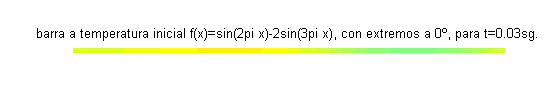    Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica

    2. También podemos dibujar la función temperatura frente a la posición, para distintos valores del tiempo. En la siguiente gráfica se muestran 11 funciones temperatura correspondientes a 11 valores del tiempo, entre $t=0$ (la primera, dibujada en azul) y $t=0.05$ (la más cercana al eje horizontal, en color naranja):

    Gráfica

  2. En este apartado se pide el recíproco a lo comentado arriba. Ahora se obtienen las funciones del tiempo correspondientes a varios valores de la variable $x$, (posición):
    • $k=0$, $x_0=0$, $u_0(t)=u(0,t)=0$
    • $k=1$, $x_1=\frac{1}{4}$, $u_1(t)=u(\frac{1}{4},t)=e^{-4\pi^2t}-\sqrt{2}e^{-9\pi^2t}$
    • $k=2$, $x_2=\frac{1}{2}$, $u_2(t)=u(\frac{1}{2},t)=2e^{-9\pi^2t}$
    • $k=3$, $x_3=\frac{3}{4}$, $u_3(t)=u(\frac{3}{4},t)=-e^{-4\pi^2t}-\sqrt{2}e^{-9\pi^2t}$
    • $k=4$, $x_4=1$, $u_4(t)=u(1,t)=0$

    En la siguiente figura representamos las funciones $u_1(t)$, $u_2(t)$ y $u_3(t)$: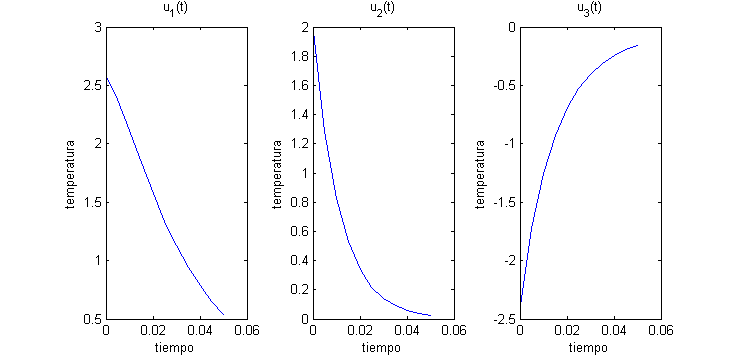

    Gráfica

       t=0:.005:.05;
   exp1=exp(-4*pi^2*t);exp2=exp(-9*pi^2*t); %% definimos exp1 y exp2 pues se utilizan en las tres funciones
   figure(1)
   % se dibujan las gráficas de las funciones u_1, u_2 y u_3
   subplot(1,3,1)
   plot(t,4*exp1-sqrt(2)*exp2)
   title('u_1(t)')
   xlabel('tiempo');ylabel('temperatura')
   subplot(1,3,2)
   plot(t,2*exp2)
   title('u_2(t)')
   xlabel('tiempo');ylabel('temperatura')
   subplot(1,3,3)
   plot(t,-exp1-sqrt(2)*exp2)
   title('u_3(t)')
   xlabel('tiempo');ylabel('temperatura')

Ejercicio 7

Continuando con las funciones $u_k(t)$ del ejercicio anterior, llamemos $h$ a la distancia entre cada par de nodos $x_i$, es decir, $h=1/4$,
  1. analiza gráficamente cuánto se parecen las funciones $$\frac{du_1}{dt} \hspace{.7cm} \mbox{y} \hspace{.7cm} v_1=\frac{u_2-2u_1+u_0}{h^2}$$
  2. idem para las funciones $$\frac{du_2}{dt} \hspace{.7cm} \mbox{y} \hspace{.7cm} v_2=\frac{u_3-2u_2+u_1}{h^2}$$
  3. idem para las funciones $$\frac{du_3}{dt} \hspace{.7cm} \mbox{y} \hspace{.7cm} v_3=\frac{u_4-2u_3+u_2}{h^2}$$
Solución
  1. Por una parte, $$u_1(t)=e^{-4\pi^2t}-\sqrt{2}e^{-9\pi^2t}\hspace{.6cm}\Rightarrow\hspace{.6cm} \frac{du_1}{dt}=-4\pi^2e^{-4\pi^2t}+9\pi^2\sqrt{2}e^{-9\pi^2t}$$ y por otra, puesto que $u_2(t)=2e^{-9\pi^2t}$ y $u_0(t)=0$, $$v_1=\frac{u_2-2u_1+u_0}{h^2}=16(-2e^{-4\pi^2t}+2(1+\sqrt{2})e^{-9\pi^2t})=32(-e^{-4\pi^2t}+(1+\sqrt{2})e^{-9\pi^2t})$$ Ahora representamos $u'_1(t)$ y $v_1(t)$, con 
    	t=linspace(0,.05,30);
	exp1=exp(-4*pi^2*t);exp2=exp(-9*pi^2*t);
	plot(t,pi^2*(-4*exp1+9*sqrt(2)*exp2),t,32*(-exp1+(1+sqrt(2))*exp2))
	legend('derivada de u_1','aproximación')
	xlabel('tiempo')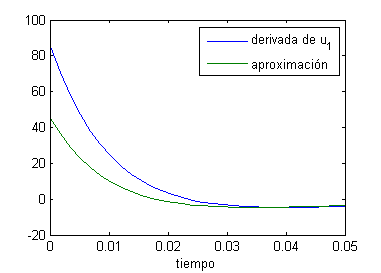

    Gráfica

  2. Derivando $u_2(t)$, $$\frac{du_2}{dt}=-18\pi^2e^{-9\pi^2t}$$ y puesto que $u_3(t)=-e^{-4\pi^2t}-\sqrt{2}e^{-9\pi^2t}$, la aproximación resulta $$v_2=\frac{u_3-2u_2+u_1}{h^2}=-16(2\sqrt{2}+4)e^{-9\pi^2t}=-32(\sqrt{2}+2)e^{-9\pi^2t}$$ Ahora representamos $u'_2(t)$ y $v_2(t)$, con 
    	t=linspace(0,.05,30);
	exp1=exp(-4*pi^2*t);exp2=exp(-9*pi^2*t);
	plot(t,-18*pi^2*exp2,t,-32*(2+sqrt(2))*exp2)
    legend('derivada de u_2','aproximación')
	xlabel('tiempo')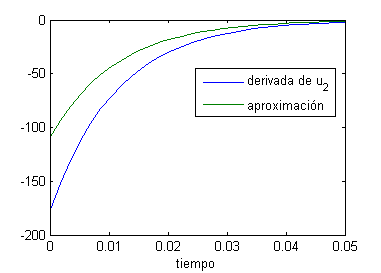

    Gráfica

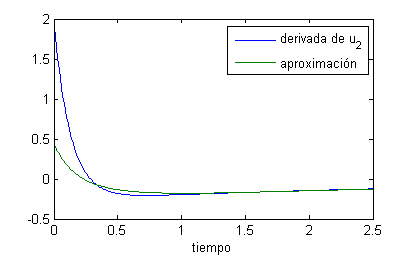
  3. Derivando $u_3(t)$, $$\frac{du_3}{dt}=4\pi^2e^{-4\pi^2t}+9\pi^2\sqrt{2}e^{-9\pi^2t}$$ y, teniendo en cuenta que $u_4(t)=0$, la aproximación resulta $$v_3=\frac{u_4-2u_3+u_2}{h^2}=16(2e^{-4\pi^2t}+(2+2\sqrt{2})e^{-9\pi^2t})=32(e^{-4\pi^2t}+(1+\sqrt{2})e^{-9\pi^2t})$$ Ahora representamos $u'_3(t)$ y $v_3(t)$, con 
    		t=linspace(0,.05,30);
		exp1=exp(-4*pi^2*t);exp2=exp(-9*pi^2*t);
		plot(t,pi^2*(4*exp1+9*sqrt(2)*exp2),t,32*(exp1+(1+sqrt(2))*exp2))
		legend('derivada de u_3','aproximación')
		xlabel('tiempo')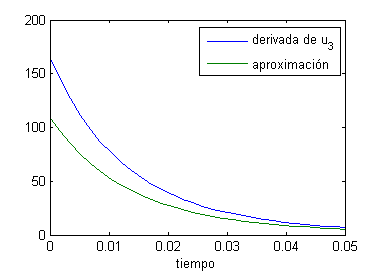

    Gráfica

Ejercicio 8

  1. Comprueba que la función $$u(x,t)=e^{-t/4}\cos \frac{x}{2}-e^{-9t/4}\cos \frac{3x}{2}$$ es solución del problema $$\left\{\begin{array}{lll} \frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial x^2}, & 0<x<\pi, & t>0\\ \frac{\partial u}{\partial x}(0,t)=0, & & t>0 \\ u(\pi,t)=0, & & t>0 \\ u(x,0)=\cos\frac{x}{2}-\cos \frac{3x}{2}, & 0\leq x \leq \pi & \end{array}\right.$$
  2. Si llamamos $u_k(t)=u(x_k,t)$, escribe las cuatro funciones $u_k(t)$, para $k=0,\, 1,\, 2,\, 3$ siendo $x_k=k\pi/3$.
Solución
  1. Derivando $u(x,t)=e^{-t/4}\cos \frac{x}{2}-e^{-9t/4}\cos \frac{3x}{2}$ respecto de $t$, $$u'_t(x,t)=\frac{-1}{4}e^{-t/4}\cos \frac{x}{2}+\frac{9}{4}e^{-9t/4}\cos \frac{3x}{2}$$ obtenemos lo mismo que derivándola dos veces respecto de $x$. Además esta función cumple $u'_x(0,t)=0$, $u(\pi,t)=0$ y $u(x,0)=\cos \frac{x}{2}-\cos \frac{3x}{2}$.

    Esta función puede interpretarse como la temperatura de una varilla o barra delgada de longitud $\pi$, aislada lateralmente y en su extremo izquierdo (el correspondiente a $x=0$) y cuyo extremo derecho (el correspondiente a $x=\pi$), se mantiene a cero grados; la temperatura inicial de cada punto $x$ de la barra viene dada por $\cos \frac{x}{2}-\cos \frac{3x}{2}$. Podemos representar la barra coloreada según su temperatura para distintos valores del tiempo:

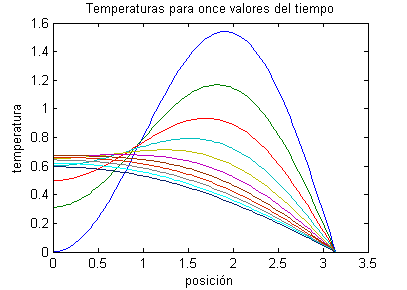
    Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica

    También podemos representar las gráficas de las funciones temperatura frente a la posición para estos once valores del tiempo; la curva azul (pasando por el origen) corresponde a $t=0$ y la gris oscura corresponde a $t=2$.

    Gráfica

  2. En este apartado hemos de escribir las funciones temperatura, respecto del tiempo, correspondientes a cuatro posiciones:
    • $k=0$, $x_0=0$, $u_0(t)=u(0,t)=e^{-t/4}-e^{-9t/4}$
    • $k=1$, $x_1=\frac{\pi}{3}$, $u_1(t)=u(\frac{\pi}{3},t)=\frac{\sqrt{3}}{2}e^{-t/4}$
    • $k=2$, $x_2=\frac{2\pi}{3}$, $u_2(t)=u(\frac{2\pi}{3},t)=\frac{1}{2}e^{-t/4}+e^{-9t/4}$
    • $k=3$, $x_3=\pi$, $u_3(t)=u(\pi,t)=0$
    Podemos representar $u_0(t)$, $u_1(t)$ y $u_2(t)$ con 
    t=0:.01:2;
 exp1=exp(-t/4);exp2=exp(-9*t/4);
figure(1)
% se dibujan las gráficas de las funciones u_0, u_1 y u_2
subplot(1,3,1)
plot(t,exp1-exp2)
title('u_0(t)')
xlabel('tiempo');ylabel('temperatura')
subplot(1,3,2)
plot(t,sqrt(3)*exp1/2)
title('u_1(t)')
xlabel('tiempo');ylabel('temperatura')
subplot(1,3,3)
plot(t,exp1/2+exp2)
title('u_2(t)')
xlabel('tiempo');ylabel('temperatura')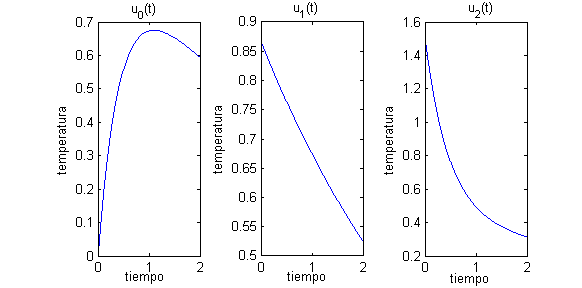

    Gráfica

Ejercicio 9

Continuando con las funciones del ejercicio anterior, para $h=\pi/3$
  1. analiza gráficamente cuánto se parecen las funciones $$\frac{du_1}{dt} \hspace{.7cm} \mbox{y} \hspace{.7cm} v_1=\frac{2(u_2-u_1)}{3h^2}$$
  2. idem para las funciones $$\frac{du_2}{dt} \hspace{.7cm} \mbox{y} \hspace{.7cm} v_2=\frac{u_3-2u_2+u_1}{h^2}$$
Solución
Puesto que $u_1(t)=\frac{\sqrt{3}}{2}e^{-t/4}$, $u_2(t)=\frac{1}{2}e^{-t/4}+e^{-9t/4}$ y $u_3(t)=0$,
  1. Derivando se tiene, $$\frac{du_1}{dt}=-\frac{\sqrt{3}}{8}e^{-t/4}$$ y la aproximación es $$v_1=\frac{2(u_2-u_1)}{3h^2}=\frac{6}{\pi^2}\left(\frac{1-\sqrt{3}}{2}e^{-t/4}+e^{-9t/4}\right)$$ Representamos $u'_1$ y $v_1$ con 
    t=0:.01:2;
exp1=exp(-t/4);exp2=exp(-9*t/4);
plot(t,-sqrt(3)*exp1/8,t,6*((1-sqrt(3))*exp1/2+exp2)/pi^2)
legend('derivada de u_1','aproximación')
xlabel('tiempo')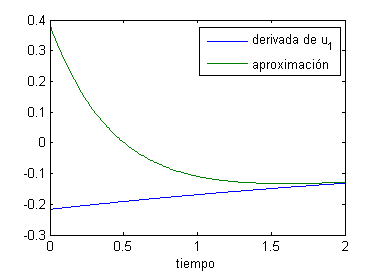

    Gráfica

  2. Para la función $u_2$, la derivada es $$\frac{du_2}{dt}=\frac{-1}{8}e^{-t/4}-\frac{9}{4}e^{-9t/4}$$ y la aproximación de esta derivada, $$v_2=\frac{u_3-2u_2+u_1}{h^2}=\frac{9}{\pi^2}\left(\left(\frac{\sqrt{3}}{2}-1\right)e^{-t/4}-2e^{-9t/4}\right)$$ Representamos $u'_2$ y $v_2$ con 
    	 t=0:.01:2;
	 exp1=exp(-t/4);exp2=exp(-9*t/4);
	 plot(t,-exp1/8-9*exp2/4,t,9*((sqrt(3)/2-1)*exp1-2*exp2)/pi^2)
	 legend('derivada de u_2','aproximación')
	 xlabel('tiempo')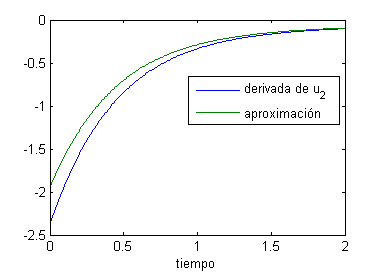

    Gráfica

Ejercicio 10

  1. Comprueba que la función $$u(x,t)=e^{-\pi^2t/32}\mbox{sen} \frac{\pi x}{4}+\frac{1}{2}e^{-9\pi^2 t/32}\mbox{sen} \frac{3\pi x}{4}+\frac{1}{3}e^{-25\pi^2 t/32}\mbox{sen} \frac{5\pi x}{4}$$ es solución del problema siguiente para $c=.5$ $$\left\{\begin{array}{lll} \frac{\partial u}{\partial t}=c\frac{\partial^2 u}{\partial x^2}, & 0<x<2, & t>0\\ u(0,t)=0, & & t>0 \\ \frac{\partial u}{\partial x}(2,t)=0, & & t>0 \\ u(x,0)=\mbox{sen}\frac{\pi x}{4}+\frac{1}{2}\mbox{sen} \frac{3\pi x}{4}+\frac{1}{3}\mbox{sen} \frac{5\pi x}{4}, & 0\leq x \leq 2 & \end{array}\right.$$
  2. Si llamamos $u_k(t)=u(x_k,t)$, escribe las cuatro funciones $u_k(t)$, para $k=0,\, 1,\, 2,\, 3$ siendo $x_k=2k/3$.
Solución
  1. Derivando respecto de $t$, $$ \frac{\partial u}{\partial t}=\frac{-\pi^2}{32}e^{-\pi^2t/32}\mbox{sen} \frac{\pi x}{4}+\frac{-9\pi^2}{64}e^{-9\pi^2 t/32}\mbox{sen} \frac{3\pi x}{4}+\frac{25\pi^2}{96}e^{-25\pi^2 t/32}\mbox{sen} \frac{5\pi x}{4}$$ y derivando dos veces respecto de $x$, $$\frac{\partial^2 u}{\partial x^2}=\frac{-\pi^2}{16}e^{-\pi^2t/32}\mbox{sen} \frac{\pi x}{4}+\frac{-9\pi^2}{32}e^{-9\pi^2 t/32}\mbox{sen} \frac{3\pi x}{4}+\frac{25\pi^2}{48}e^{-25\pi^2 t/32}\mbox{sen} \frac{5\pi x}{4}$$ luego en efecto $u$ es solución de la ecuación $u'_t=u''_{xx}/2$. También podemos comprobar fácilmente que $u(0,t)=0$, $\frac{\partial u}{\partial x}(2,t)=0$ y $u(x,0)=\mbox{sen}\frac{\pi x}{4}+\frac{1}{2}\mbox{sen} \frac{3\pi x}{4}+\frac{1}{3}\mbox{sen} \frac{5\pi x}{4}$. Esta función $u(x,t)$ puede interpretarse como la temperatura de una varilla o barra delgada de longitud 2, aislada lateralmente y en su extremo derecho, con el extremo izquierdo permaneciendo a cero grados y cuya temperatura inicial es $\mbox{sen}\frac{\pi x}{4}+\frac{1}{2}\mbox{sen} \frac{3\pi x}{4}+\frac{1}{3}\mbox{sen} \frac{5\pi x}{4}$:

    Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica Gráfica

    Las gráficas de las funciones temperatura respecto de la posición para distintos valores del tiempo, comprendidos entre $t=0$ (curva azul) y $t=2.5$ (curva gris oscuro) son: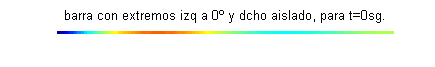

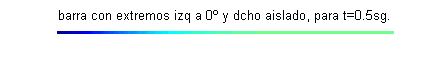
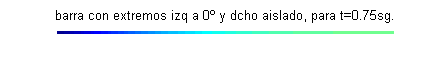
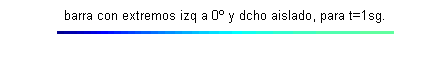
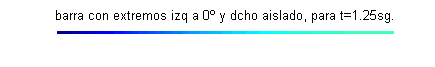
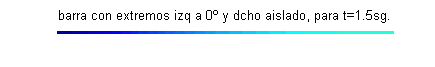
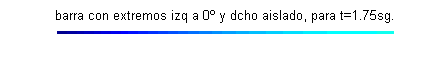
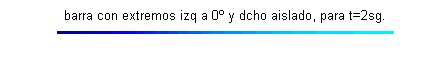
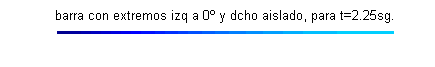
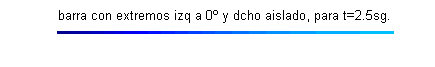
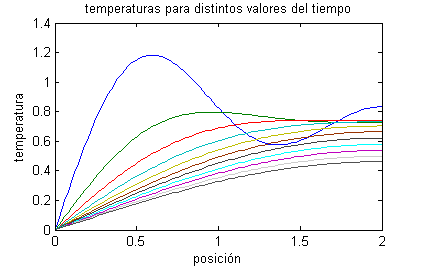
    Gráfica

  2. En este apartado procedemos reciprocamente, pues debemos fijar varios valores de la posición obteniendo la función temperatura respecto del tiempo:
    • $k=0$, $x_0=0$, $u_0(t)=u(0,t)=0$
    • $k=1$, $x_1=\frac{2}{3}$, $u_1(t)=u(\frac{2}{3},t)=\frac{1}{2}e^{-\pi^2t/32}+\frac{1}{2}e^{-9\pi^2t/32}+\frac{1}{6}e^{-25\pi^2t/32}$
    • $k=2$, $x_2=\frac{4}{3}$, $u_2(t)=u(\frac{4}{3},t)=\frac{\sqrt{3}}{2}e^{-\pi^2t/32}-\frac{\sqrt{3}}{6}e^{-25\pi^2t/32}$
    • $k=3$, $x_3=2$, $u_3(t)=u(2,t)=e^{-\pi^2t/32}-\frac{1}{2}e^{-9\pi^2t/32}+\frac{1}{3}e^{-25\pi^2t/32}$
    Representamos las funciones $u_1(t)$, $u_2(t)$ y $u_3(t)$ con: 
              t=0:.01:2.5;
		  exp1=exp(-pi^2*t/32);exp2=exp(-9*pi^2*t/32);exp3=exp(-25*pi^2*t/32);
		  % se dibujan las gráficas de las funciones u_1, u_2 y u_3
		  subplot(1,3,1)
		  plot(t,exp1/2+exp2/2+exp3/6)
		  title('u_1(t)')
		  xlabel('tiempo');ylabel('temperatura')
		  subplot(1,3,2)
		  plot(t,sqrt(3)*(exp1/2-exp3/6))
		  title('u_2(t)')
		  xlabel('tiempo');ylabel('temperatura')
		  subplot(1,3,3)
		  plot(t,exp1-exp2/2+exp3/3)
		  title('u_3(t)')
		  xlabel('tiempo');ylabel('temperatura')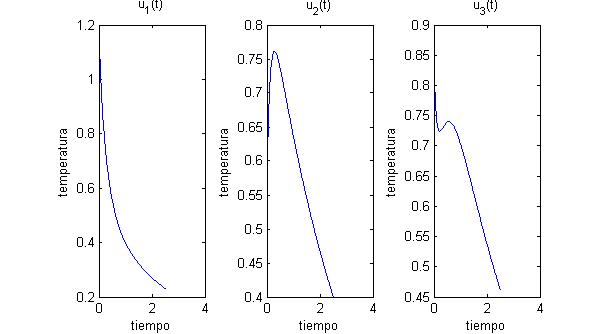

    Gráfica

Ejercicio 11

Continuando con las funciones del ejercicio anterior, para $h=2/3$,
  1. analiza gráficamente cuánto se parecen las funciones $$\frac{du_1}{dt} \hspace{.7cm} \mbox{y} \hspace{.7cm} v_1=\frac{c(u_2-2u_1+u_0)}{h^2}$$
  2. idem para las funciones $$\frac{du_2}{dt} \hspace{.7cm} \mbox{y} \hspace{.7cm} v_2=\frac{2c(u_1-u_2)}{3h^2}$$
Solución
Puesto que $u_0(t)=0$ y $$u_1(t)=\frac{1}{2}e^{-\pi^2t/32}+\frac{1}{2}e^{-9\pi^2t/32}+\frac{1}{6}e^{-25\pi^2t/32}$$ $$u_2(t)=\frac{\sqrt{3}}{2}e^{-\pi^2t/32}+\frac{-\sqrt{3}}{6}e^{-25\pi^2t/32}$$
  1. la derivada de $u_1$ es $$\frac{du_1}{dt}=\frac{-\pi^2}{64}e^{-\pi^2t/32}-\frac{9\pi^2}{64}e^{-9\pi^2t/32}-\frac{25\pi^2}{192}e^{-25\pi^2t/32}$$ y la aproximación de esta derivada, $$v_1=\frac{c(u_2-2u_1+u_0)}{h^2}=\frac{9}{8}\left(\frac{\sqrt{3}-2}{2}e^{-\pi^2t/32}- e^{-9\pi^2t/32}-\frac{\sqrt{3}+2}{2}e^{-25\pi^2t/32}\right)$$ Representamos $u'_1$ y $v_1$ con 
      t=0:.01:2.5;
   exp1=exp(-pi^2*t/32);exp2=exp(-9*pi^2*t/32);exp3=exp(-25*pi^2*t/32);
   plot(t,-pi^2*(exp1+9*exp2+25*exp3/3)/64,t,9*((sqrt(3)-2)*exp1/2-exp2-(sqrt(3)+2)*exp3/6)/8)
   legend('derivada de u_1','aproximación')
   xlabel('tiempo')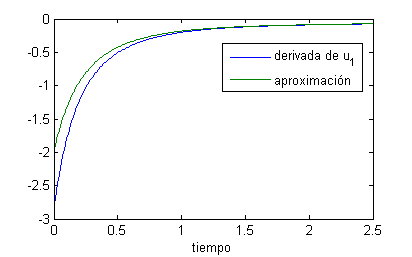

    Gráfica

  2. derivando $u_2$, $$\frac{du_2}{dt}=\frac{-\sqrt{3}\pi^2}{64}e^{-\pi^2t/32}+\frac{25\sqrt{3}\pi^2}{192}e^{-25\pi^2t/32}$$ y la aproximación es $$v_2=\frac{2c(u_1-u_2)}{3h^2}=\frac{3(1-\sqrt{3})}{8}e^{-\pi^2t/32}+\frac{3}{8}e^{-9\pi^2t/32}+\frac{1+\sqrt{3}}{8}e^{-25\pi^2t/32}$$ Representamos $u'_2$ y $v_2$ con 
      t=0:.01:2.5;
   exp1=exp(-pi^2*t/32);exp2=exp(-9*pi^2*t/32);exp3=exp(-25*pi^2*t/32);
   plot(t,sqrt(3)*pi^2*(-exp1/64+25*exp3/192),t,(3*(1-sqrt(3))*exp1+3*exp2+(sqrt(3)+1)*exp3)/8)
legend('derivada de u_2','aproximación')
   xlabel('tiempo')

    Gráfica