Enunciado
La ecuación de Duffing
$$y''+y+ry^3=0$$
donde $r$ es una constante, modeliza las vibraciones de una masa sujeta a un resorte en un caso no lineal. Vamos a observar que la solución del problema formado por esa ecuación y unas condiciones iniciales, $y(0)=a$, $y'(0)=0$, tiene oscilaciones y que éstas cambian de periodo cuando varía el parámetro $r$ y cambian de periodo y de amplitud con el valor $a$.
- Escribe el sistema diferencial de primer orden equivalente al problema inicial
$$y''+y+ry^3=0 \ ,\ \ y(0)=a \ ,\ \ y'(0)=0$$
- Prepara una función en el ordenador con dos variables de entrada, $r$ y $a$, y una de salida que sea el vector columna formado por los valores estimados de $y(t)$ para $t$ entre 0 y 10.
- Prepara una función con dos variables de entrada, un vector de valores de $r$ y $a$, que dibuje (en una misma gráfica) la estimación de $y(t)$ para $t$ entre 0 y 10 para los diferentes valores de $r$ contenidos en el vector de entrada. Pruébala para tres valores diferentes de $r$.
- Prepara una función con dos variables de entrada, $r$ y un vector de valores de $a$, que dibuje (en una misma gráfica) la estimación de $y(t)$ para $t$ entre 0 y 10 para los diferentes valores de $a$ contenidos en el vector de entrada. Pruébala para tres valores diferentes de $a$.
Resolución del primer apartado
Como en ejercicios anteriores, para encontrar el sistema diferencial de primer orden equivalente al p.v.i. dado haremos $$x_1(t)=y(t) \hspace{.5cm}, \hspace{.5cm} x_2(t)=y'(t)$$
Escribe el sistema y pulsa en 'Ver'.
Ver
El sistema resultante, equivalente al p.v.i es
$$\left\{\begin{array}{lll} x'_1=x_2 & , & x_1(0)=a\\ x'_2=-x_1-rx_1^3 & , & x_2(0)=0\end{array}\right.$$
Resolución del segundo apartado
Vamos a pensar ahora cómo estimaríamos la solución de ese sistema para $r=1$ y $a=1$ utilizando 'ode45' para $t$ variando desde 0 hasta 10, con paso $h=0.1$. Recuerda que los argumentos de entrada obligatorios de 'ode45' para la aproximación de la solución de un sistema diferencial de dimensión 'm' (número de incógnitas o de ecuaciones) son- la función $f$ definida previamente con la '@', que será un vector columna de 'm' funciones (las variables de esas funciones son: la variable independiente y las 'm' variables incógnitas);
- el vector fila de valores de $t$ donde quiera aproximarse la solución, que debe empezar en $t_0$
- el vector fila formado por los datos iniciales (valores de las incógnitas en $t_0$)
Ver
Con
f=@(t,x) [x(2) ; -x(1)-x(1)^3]; [t,solsis]=ode45(f,0:.1:10,[1,0]);guardará en 'solsis' las estimaciones para $x_1$ y para $x_2$ ( es decir, para $y$ y para $y'$).
Prepara ahora una función, 'auxDuffing', con dos variables de entrada ($r$ y $a$) y una de salida que sea la estimación de $y$ en los mismos valores de $t$ que antes. ¿Cuál de éstas es correcta?
function auxDuffing(r,a) f=@(t,x) [x(2) ; -x(1)-r*x(1)^3]; [t,solsis]=ode45(f,0:.1:10,[a,0]); end
function solsis=auxDuffing(r,a) f=@(t,x) [x(2) ; -x(1)-r*x(1)^3]; [t,solsis]=ode45(f,0:.1:10,[a,0]); end
Ninguna de las opciones presentadas es correcta.
No tiene variable de salida.
La variable de salida sería una matriz con las aproximaciones de $y$ y de $y'$; sólo queremos las de $y$.
En efecto, ninguna de las presentadas es la correcta. Deberíamos poner..., pulsa en 'Continuar' cuando la tengas.
En el fichero 'auxDuffing.m' escribimos
function sol=auxDuffing(r,a) f=@(t,x) [x(2) ; -x(1)-r*x(1)^3]; [t,solsis]=ode45(f,0:.1:10,[a,0]); sol=solsis(:,1); endy mejor si añadimos un comentario sobre lo que realiza la función:
function sol=auxDuffing(r,a) % utiliza ode45 para estimar la solución del p.v.i y''+y+ry^3=0, y(0)=a, % y'(0)=0; sol es el vector columna 101x1 con esa estimación f=@(t,x) [x(2) ; -x(1)-r*x(1)^3]; [t,solsis]=ode45(f,0:.1:10,[a,0]); sol=solsis(:,1); endCuando en la ventana de comandos ejecutemos
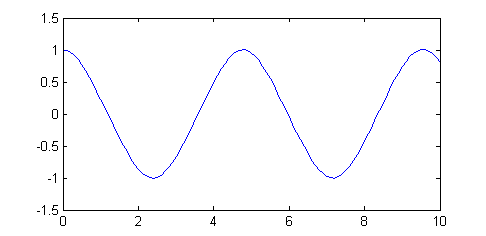
>> sol=auxDuffing(1,1); >> plot(0:.1:10,sol)en la ventana de figuras se representará la estimación del problema $$y''+y+y^3=0 \ ,\ \ y(0)=1 \ ,\ \ y'(0)=0$$ para $t$ entre 0 y 10:
Resolución del tercer apartado
En este apartado definiremos una nueva función que utilizará la función definida antes, 'auxDuffing', para dibujar las estimaciones correspondientes a varios valores de $r$ y uno fijado de $a$. Las variables de entrada de esta nueva función son por tanto el vector formado por los valores de $r$ y el valor de $a$; no tiene variable de salida y su efecto es el de dibujar tantas aproximaciones como valores de $r$ haya en el vector de entrada. Seguiremos los siguientes pasos- definir la función con sus variables de entrada;
- definir una matriz de ceros; en ella guardaremos por columnas las estimaciones de $y(t)$;
- hacer un ciclo 'for' que para cada componente del vector de valores de $r$
- calcule la estimación correspondiente ejecutando la función 'auxDuffing' con las variables de entrada apropiadas
- guarde esa estimación en una columna de la matriz definida antes;
- generar el vector de valores de $t$;
- dibujar cada columna de la matriz de estimaciones respecto del vector de valores de $t$;
- cerrar la función.
Ver
En el fichero 'ecuDuffing.m' escribimos
function ecuDuffing(vr,a)
% para los valores del parámetro r contenidos en vr se estima con ode45 la
% solución de y''+y+ry^3=0, y(0)=a, y'(0)=0 para los valores de t=0:.1:10
% las estimaciones se guardan como columnas de est, que es una matriz 101xlongitud(vr)
est=zeros(101,length(vr));
for k=1:length(vr)
sol=auxDuffing(vr(k),a);
est(:,k)=sol;
end
t=0:.1:10;
plot(t,est)
end
Si en la ventana de comandos escribimos
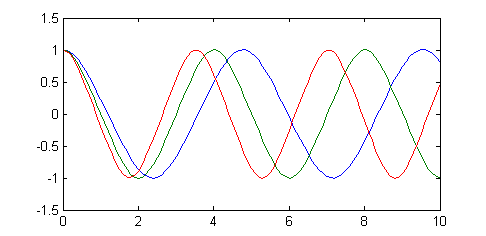
ecuDuffing(1:3,1)en la ventana de figuras veremos la representación de las estimaciones de la solución para los valores $r=1$, $r=2$ y $r=3$, (azul, verde, rojo) tomando $y(0)=1$.
Resolución del cuarto apartado
El trabajo ahora es paralelo al realizado en el apartado anterior. En este caso hemos de preparar una función que para un mismo valor de $r$, dibuje las estimaciones para distintos valores de la condición inicial $y(0)$. Habiendo resuelto el apartado anterior, éste es muy sencillo. Escribe la nueva función en un nuevo fichero y pulsa en 'Ver'.
Ver
Escribimos en el fichero 'ecuDuffing2':
function ecuDuffing2(r,va)
% para los valores 'a' contenidos en va se estima con ode45 la
% solución de y''+y+ry^3=0, y(0)=a, y'(0)=0 para los valores de t=0:.1:10
% las estimaciones se guardan como columnas de est, que es una matriz 101xlongitud(va)
est=zeros(101,length(va));
for k=1:length(va)
sol=auxDuffing(r,va(k));
est(:,k)=sol;
end
t=0:.1:10;
plot(t,est)
end
Cuando en la ventana de comandos ejecutemos
ecuDuffing2(1,1:4)obtendremos la figura