Índice de tema

 

Enunciado

En este ejercicio trabajaremos con el problema no lineal siguiente $$y''+0.1(1-y^2)y'+x=0 \ ,\ \ y(0)=y_0 \ ,\ \ y'(0)=0$$ Encuentra y representa la solución estimada con el comando 'ode45' para $t$ entre 0 y 20, tomando como paso $h=0.04$, para cada uno de los valores de $y_0$ siguientes $$y_0=0.2 \ ,\ \ y_0=2 \ ,\ \ y_0=2.12$$ La representación de las tres aproximaciones se harán en una misma figura, utilizando 'subplot'. Comprueba que en los tres casos la solución tiene oscilaciones pero que para una de las condiciones iniciales estas oscilaciones son amortiguadas, para otra condición son estacionarias y para otras son crecientes. Es decir, la estabilidad del sistema modelizado por este p.v.i. depende de la condición inicial.

Resolución

Hemos de empezar encontrando el sistema diferencial de primer orden equivalente al p.v.i. dado; recuerda que será de la forma $$\left\{\begin{array}{ll} x'_1=f_1(t,x_1,x_2) & , & x_1(t_0)=\ldots \\ x'_2=f_2(t,x_1,x_2) & , & x_2(t_0)=\ldots\end{array}\right.$$ Encuéntralo y pulsa en 'Ver' cuando lo tengas.
Ver
Tomando $$x_1(t)=y(t) \hspace{.5cm}, \hspace{.5cm} x_2(t)=y'(t)$$ el sistema resultante, equivalente al p.v.i es $$\left\{\begin{array}{lll} x'_1=x_2 & , & x_1(0)=y_0\\ x'_2=-x_1-0.1(1-x_1^2)x_2 & , & x_2(0)=0\end{array}\right.$$
Vamos a pensar ahora cómo estimaremos la solución de ese sistema para $y_0=.2$ utilizando 'ode45'. Recuerda que los argumentos de entrada obligatorios de 'ode45' para la aproximación de la solución de un sistema diferencial de dimensión 'm' (número de incógnitas o de ecuaciones) son
  • la función $f$ definida previamente con la '@', que será un vector columna de 'm' funciones (las variables de esas funciones son: la variable independiente y las 'm' variables incógnitas);
  • el vector fila de valores de $t$ donde quiera aproximarse la solución, que debe empezar en $t_0$
  • el vector fila formado por los datos iniciales (valores de las incógnitas en $t_0$)
En el caso que os ocupa tendremos que poner 
f=@(t,x1,x2) [x2 ; -x1+.1*(x1^2-1)*x2];
[t, est]=ode45(f, 0:.04:20,[.2,0]);

f=@(t,x) [x(2)  -x(1)+.1*(x(1)^2-1)*x(2)];
[t, est]=ode45(f, 0:.04:20,[.2,0]);

f=@(t,x) [x(2) ; -x(1)+.1*(x(1)^2-1)*x(2)];
[t, est]=ode45(f, 0:.04:20,.2,0);
Ninguna de las opciones es correcta. 
f=@(t,x) [x(2) ; -x(1)+.1*(x(1)^2-1)*x(2)];
[t, est]=ode45(f, 0:.04:20,[.2,0]);
La función 'f' debe depender sólo de dos variables: la variable independiente y el vector formado por todas las incógnitas $x_i$; si este vector se llama 'x', para hacer referencia a la primera de ellas, escribiremos 'x(1)',...
Cuidado, así definido 'f' es un vector fila
Los valores de las condiciones iniciales deben agruparse en un vector, que será el tercer argumento de 'ode45'
Sí hay una correcta.
En efecto, eso es lo correcto. Ejecutando esas dos líneas guardaremos en 'est' la estimación de $x_1(t)$ y de $x_2(t)$ para los valores de $t$ entre 0 y 20 con paso $h=0.04$; la primera columna de 'est' es la estimación de $x_1(t)$ y la segunda la estimación de $x_2(t)$. Si sólo necesitamos dibujar frente a esos valores de $t$ la primera, que es la función $y(t)$ del problema inicial, hemos de ... piénsalo y pulsa en 'Continuar' cuando lo tengas.
Para dibujar la primera columna de 'est' pondremos 
plot(t,est(:,1))
La ejecución de las tres líneas generará la figura

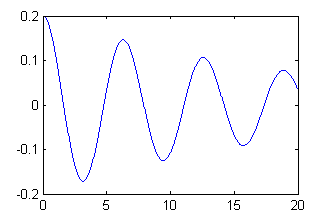
Gráfica

en la que comprobamos que efectivamente la solución tiene oscilaciones, en este caso amortiguadas.
Puesto que hemos de realizar este proceso para distintos valores de $y_0$ parece razonable generar una función que tenga como variable de entrada $y_0$ y que represente la solución aproximada correspondiente. Además, si tenemos algo de curiosidad, eso nos permitirá investigar fácilmente qué ocurre con otros valores de $y_0$ diferentes a los que nos propone el enunciado. Genera tú esa función y llámala 'oscilacionesaux'; pulsa en 'Ver' cuando la tengas.
Ver
Generalizando lo que hemos hecho antes para $y_0=.2$, escribimos 
function oscilacionesaux(y0)
%%% calcula y representa la aproximación con ode45 de la solución del p.v.i
%%% y''+0.1(1-y^2)y'+y=0, y(0)=y0, y'(0)=0
f=@(t,x) [x(2) ; -x(1)+.1*(x(1)^2-1)*x(2)];
[t, est]=ode45(f, 0:.04:20,[y0,0]);
plot(t,est(:,1))
end
Esta función auxiliar será la segunda de un fichero que se llame por ejemplo 'ejemoscilaciones', que será la que genere la figura con los tres 'subplot', en cada uno de los cuales llamaremos a 'oscilacionesaux(y0)' con un valor diferente de 'y0' para que dibuje la estimación correspodiente; podemos añadir un título en cada una que haga referencia al valor 'y0'. Piensa cómo escribirías esa función y pulsa en 'Continuar'
En el fichero 'ejemoscilaciones.m' escribiremos 
function ejemoscilaciones
%dibuja las soluciones de y''+0.1(1-y^2)y'+y=0,y(0)=y0, y'(0)=0
%correspondientes a y0=.2, y0=2 e y0=2.12
subplot(1,3,1)   %% de un vector 1x3 de gráficas, nos situamos en la primera
oscilacionesaux(.2)
title('y(0)=.2')
subplot(1,3,2)   %% de un vector 1x3 de gráficas, nos situamos en la segunda
oscilacionesaux(2)
title('y(0)=2')
subplot(1,3,3)   %% de un vector 1x3 de gráficas, nos situamos en la tercera
oscilacionesaux(2.12)
title('y(0)=2.12')
end
seguido de 
function oscilacionesaux(y0)
%%% calcula y representa la aproximación con ode45 de la solución del p.v.i
%%% y''+0.1(1-y^2)y'+y=0, y(0)=y0, y'(0)=0
f=@(t,x) [x(2) ; -x(1)+.1*(x(1)^2-1)*x(2)];
[t, est]=ode45(f, 0:.04:20,[y0,0]);
plot(t,est(:,1))
end
Cuando ejecutemos 'ejemoscilaciones.m', obtendremos la figura

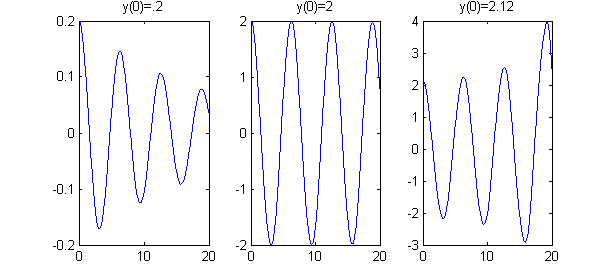
Gráfica

en la que observamos que todas las soluciones presentan oscilaciones pero éstas son
  • amortiguadas para $y_0=0.2$
  • estacionarias para $y_0=2$
  • crecientes para $y_0=2.12$
Esta última situación es altamente peligrosa, pues nuestro elemento físico llegaría más pronto o más tarde a romperse o a quemarse.