La ecuación $y''+t^2y'+3ty=t^3$ relaciona la función incógnita $y$ con su primera y segunda derivadas y con la variable indepeniente, $t$. Necesitamos dos incógnitas que sólo haya que derivar una vez, así que tomaremos $$x_1(t)=y(t) \hspace{.5cm}, \hspace{.5cm} x_2(t)=y'(t)$$ Un sistema diferencial de primer orden en las funciones $x_1(t)$ y $x_2(t)$ tiene la forma $$\left\{\begin{array}{l} x'_1=f_1(t,x_1,x_2) \\ x'_2=f_2(t,x_1,x_2) \end{array}\right.$$ Escribe el sistema diferencial de primer orden en las funciones $x_1(t)$ y $x_2(t)$ equivalente a la ecuación $y''+t^2y'+3ty=t^3$ y pulsa en 'Ver' cuando lo tengas.

El sistema de primer orden equivalente al problema de valor inicial del enunciado es $$\left\{\begin{array}{lll} x'_1=x_2 & , & x_1(0)=0\\ x'_2=t^3-3x_1-t^2x_2 & , & x_2(0)=1\end{array}\right.$$ Continuar

Resolución del segundo apartado

Para preparar una función que aproxime la solución de un sistema diferencial mediante el método de Euler podemos tomar como punto de partida el que realizamos en un ejercicio del tema de ecuaciones diferenciales de primer orden:

function yaprox=aproxEuler(f,h,x0,y0,xf)
nmax=round((xf-x0)/h);
x=x0:h:xf;
y=y0*ones(size(x));
for n=1:nmax
    y(n+1)=y(n)+h*f(x(n),y(n));
end
yaprox=y(2:end);
plot(x,y,'-*')
end

En primer lugar vamos a cambiar los nombres de las variables para adaptarlos a las que utilizamos en sistemas: $t$ es la variable independiente y $x$ reúne las dos variables incógnitas, $x_1$ y $x_2$. Con esta notación la función es

function xaprox=aproxEuler(f,h,t0,x0,tf)
nmax=round((tf-t0)/h);
t=t0:h:tf;
x=x0*ones(size(t));
for n=1:nmax
    x(n+1)=x(n)+h*f(t(n),x(n));
end
xaprox=x(2:end);
plot(t,x,'-*')
end

Vamos ahora a adaptar este código a sistemas de ecuaciones. Se irán sugiriendo las modificaciones necesarias y deberás ir pulsando 'Continuar' cuando hayas realizado cada una. Empezamos con:

• Debemos ponerle un nombre que nos recuerde a sistemas, por ejemplo, 'aproxEulersist'; no olvides cambiar también el nombre del fichero donde guardas esta función.

Continuar

function xaprox=aproxEulersist(f,h,t0,x0,tf)

• No cambiaremos los nombres de las variables de entrada y salida, aunque hemos de tener en cuenta que
  • 'xaprox' será una matriz de dos columnas (una para la aproximación de $x_1$ y otra para la aproximación de $x_2$);
  • 'f' será un vector de dos componentes formado por $f_1$ y $f_2$;
  • 'x0' será el vector de dos componentes formado por $x_1(t_0)$ y $x_2(t_0)$.
• También dejaremos igual el cálculo de 'nmax' y la definición del vector 't'.
• Quitaremos la inicialización de 'x' y sustituiremos esa fila por una en que guardemos en la primera fila de una matriz 'x', de dimensiones '(nmax+1) x 2', el vector 'x0'

Continuar

x(1,:)=x0;

• Entramos ahora en el ciclo 'for'; la asignación que se hacía para 'x(n+1)' la debemos hacer ahora para las dos columnas de la fila 'n+1', utilizando claro está la fila anterior.

Continuar

x(n+1,:)=x(n,:)+h*f(t(n),x(n,:));

• Si queremos que la variable de salida, 'xaprox', contenga las aproximaciones para los valores estrictamente superiores a $t_0$ (es decir, $t_0+h$ en adelante) la definiremos para que contenga las filas entre la 2 y la 'nmax+1' de 'x'.

Continuar

xaprox=x(2:nmax+1,:)

• Finalmente podemos dejar la línea del plot, para dibujar las aproximaciones de $x_1$ y de $x_2$, tal como está. El efecto es una figura con la representación de los valores de cada columna de 'x' frente a 't', en azul la primera columna (aproximación de $x_1$) y en verde la segunda (aproximación de $x_2$). El código completo (a falta de los comentarios) es

function xaprox=aproxEulersist(f,h,t0,x0,tf)
nmax=round((tf-t0)/h);
t=t0:h:tf;
x(1,:)=x0;
for n=1:nmax
    x(n+1,:)=x(n,:)+h*f(t(n),x(n,:));
end
xaprox=x(2:nmax+1,:);
plot(t,x,'-*')
end

Continuar

Para probar este código podemos ejecutarlo poniendo

>> f=@ (t,x) [x(2) t^3-3*t*x(1)-t^2*x(2)];  %%% definición de la función f
>> xaprox=aproxEulersist(f,1/8,0,[0 1],1)

Obtendremos en la ventana de comandos

xaprox =

    0.1250    1.0000
    0.2500    0.9924
    0.3741    0.9632
    0.4945    0.9003
    0.6070    0.7950
    0.7064    0.6445
    0.7869    0.4532
    0.8436    0.2354
    

y en la ventana de figuras

Continuar

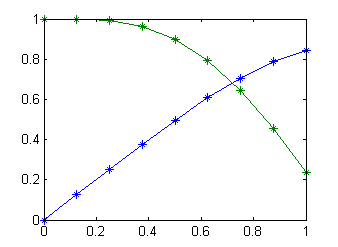
Pero puesto que hemos de comparar los valores obtenidos para $x_1$ (que es la función incógnita $y$ del problema de valor inicial) con los que se obtienen con el polinomio de Taylor de esa solución, mejor trabajaremos en un fichero. En un ejercicio anterior se había comprobado cómo la aproximación con este polinomio era muy aceptable (el mayor error ronda las $0.4$ milésimas) así que es razonable tomarlo como una buena solución. En este fichero incluiremos las líneas con las que se calculan ambas aproximaciones (con Taylor y con Euler) y la diferencia entre ambas. Intenta escribirlo y pulsa en 'Ver' cuando lo tengas.

vt=1/8:1/8:1;
yest0=vt-vt.^4/3+vt.^5/20+vt.^7/18-vt.^8/140-vt.^10/162+vt.^11/1400; %% aprox. con Taylor, vector fila 1x8
f=@ (t,x) [x(2) t^3-3*t*x(1)-t^2*x(2)];
xest1=aproxEulersist(f,.125,0,[0,1],1) ; % método de Euler
yest1=xest1(:,1);   % tomamos la primera columna de xest1, es un vector columna 8x1
comp1=abs(yest0-yest1')

comp1 =

    0.0001    0.0012    0.0052    0.0133    0.0262    0.0436    0.0638    0.0840

Resolución del tercer apartado

Debemos repetir el apartado anterior pero con el método de Euler mejorado aplicado a sistemas diferenciales de primero orden. Tomaremos como punto de partida la función 'aproxEulersist' definida en el apartado anterior. Empezamos haciendo una copia del fichero que la contiene, guardándolo con el nombre 'aproxEulermejsist', nombre que igualmente pondremos a la nueva función. Después, lo único que hay que modificar es el cuerpo del ciclo 'for':

function xaprox=aproxEulermejsist(f,h,t0,x0,tf)
nmax=round((tf-t0)/h);
t=t0:h:tf;
x(1,:)=x0;
for n=1:nmax
      aux(n,:)=x(n,:)+h*f(t(n),x(n,:));
      x(n+1,:)=x(n,:)+h*(f(t(n),x(n,:))+f(t(n+1),aux(n,:)))/2;
end
xaprox=x(2:nmax+1,:);
plot(t,x,'-*')
end

Continuar

Ahora debemos añadir al fichero en el que se calcularon las aproximaciones del apartado anterior las líneas apropiadas para que calcule la aproximación de la solución del problema del enunciado y lo compare con la estimación con Taylor. Inténtalo y pulsa en 'Ver'.

xest2=aproxEulermejsist(f,.125,0,[0,1],1) ; % método de Euler mejorado
yest2=xest2(:,1);
comp2=abs(yest0-yest2')

comp1 =

    0.0001    0.0012    0.0052    0.0133    0.0262    0.0436    0.0638    0.0840


comp2 =

    0.0001    0.0003    0.0006    0.0010    0.0013    0.0013    0.0011    0.0006
    

Resolución del cuarto apartado

Por último vamos a estimar la solución del sistema que nos ocupa, $$\left\{\begin{array}{lll} x'_1=x_2 & , & x_1(0)=0\\ x'_2=t^3-3x_1-t^2x_2 & , & x_2(0)=1\end{array}\right.$$ asociado al problema de valor inicial $$y''+t^2y'+3ty=t^3 \ \ ,\ \ y(0)=0\ \ ,\ \ y'(0)=1$$ mediante el método de Runge-Kutta implementado en el comando 'ode45'. Los argumentos de entrada obligatorios de 'ode45' para la aproximación de la solución de un sistema diferencial de dimensión 'm' (número de incógnitas o de ecuaciones) son

• la función $f$ definida previamente con la '@', que será un vector de 'm' funciones (las variables de esas funciones son: la variable independiente y las 'm' variables incógnitas); IMPORTANTE: este vector de funciones es un vector columna, dimensión mx1
• el vector fila de valores de $t$ donde quiera aproximarse la solución, que debe empezar en $t_0$
• el vector fila formado por los datos iniciales (valores de las incógnitas en $t_0$)

En nuestro caso, la dimensión $m$ es 2, $t_0=0$, queremos la aproximación en los valores $1/8$, $1/4$, $3/8$, ... , $7/8$ y $1$ y el vector de valores iniciales es $[0,1]$:

f=@ (t,x) [x(2); t^3-3*t*x(1)-t^2*x(2)];  %vector columna con funciones del sistema
[t,xest3]=ode45(f,0:1/8:1,[0,1]);  % xest3 es una matriz 9x2

Escribe las líneas que añadimos a nuestro fichero para hallar esa aproximación y compararla con la de Tylor; pulsa en 'Ver' cuando lo tengas.

f=@ (t,x) [x(2); t^3-3*t*x(1)-t^2*x(2)];  %vector columna con funciones del sistema
[t,xest3]=ode45(f,0:1/8:1,[0,1]);  % xest3 es una matriz 9x2
yest3=xest3(2:9,1);                % tomamos las filas 2 a 9 de la primera columna
comp3=abs(yest0-yest3')            % comparamos con los valores obtenidos con Taylor

comp1 =

    0.0001    0.0012    0.0052    0.0133    0.0262    0.0436    0.0638    0.0840


comp2 =

    0.0001    0.0003    0.0006    0.0010    0.0013    0.0013    0.0011    0.0006


comp3 =

  1.0e-003 *

    0.0000    0.0000    0.0000    0.0001    0.0010    0.0110    0.0786    0.4302