Búsqueda de la ecuación y de soluciones bajo ciertas condiciones

Enunciado

Halla mediante eliminación de los parámetros, la ecuación de segundo orden cuya solución general es $$y(x)=C_1x^2+C_2\frac{1}{x}+3x-2 \hspace{.7cm}, \hspace{1cm} C_1, C_2\in{\bf R}$$

Escribe la expresión de la familia uniparamétrica de curvas solución de la ecuación hallada en el apartado anterior que pasan por el punto $P(1,0)$. Dibuja en el ordenador, para $x\in[0.5,1.5]$ las tres correspondientes a las pendientes $-1$, $0$ y $1$ (el punto $P$).

Para la misma ecuación, halla la familia uniparamétrica de soluciones que tienen pendiente $1/2$ en los puntos de corte con el eje $x=1$. De entre éstas, dibuja para $x\in[0.5,1.5]$ las siete correspondientes a los puntos $P_m(1,m)$ para $m=-3:3$.

Continuando con la misma ecuación, halla las soluciones que alcanzan un extremo (mínimo o máximo) cuando se cortan con $x=2$. Halla y representa dos que alcanzan máximo y dos que alcanzan mínimo. Encuentra y representa una que tenga un mínimo (cuando se corta con $x=2$) y éste sea mayor que 5 y menor que 10.

Resolución del primer apartado

Debemos hallar una expresión que relacione la función $y(x)$ con sus derivadas primera y segunda, así que parece esencial derivar $y(x)$ dos veces. Después entre las tres expresiones (la de $y(x)$, la de $y'(x)$ y la de $y''(x)$) eliminaremos los parámetros $C_1$ y $C_2$. Inténtalo y pulsa en 'Ver' cuando lo tengas.

Ver

$$y(x)=C_1x^2+C_2\frac{1}{x}+3x-2 \hspace{1cm} \Rightarrow \hspace{1cm} y'(x)=2C_1x-C_2\frac{1}{x^2}+3 \hspace{1cm} \Rightarrow \hspace{1cm} y''(x)=2C_1+2C_2\frac{1}{x^3}$$ Para eliminar los parámetros podemos proceder siempre por sustitución, pero en este caso también podemos observar que si multiplicamos la última expresión por $x^2/2$ resultará la parte de $y(x)$ que contiene las constantes $C_1$ y $C_2$: $$\frac{x^2}{2}y''(x)=C_1x^2+C_2\frac{1}{x} \hspace{1cm} \Rightarrow \hspace{1cm} x^2y''(x)=2(y(x)-3x+2)$$ con lo que la ecuación debe ser $$x^2y''(x)-2y(x)=2(2-3x)$$

Resolución del segundo apartado

Paso 1

Para encontrar las curvas solución de la ecuación anterior que pasan por el punto $P(1,0)$, debemos

Sustituir $x=1$, $y=1$ en la ecuación e integrar lo que resulte para $y''$

Resolver la ecuación y luego imponer que $y(1)=0$

Una opción es una barbaridad y la otra no es apropiada.

Eso es una barbaridad.

¿Para qué vamos a resolver la ecuación si ya conocemos su solución general?

En efecto, en este caso no nos hace falta resolver, pues en el primer apartado del ejercicio partimos de la solución general para hallar la ecuación. Debemos imponer a esa familia que $y(1)=0$. Hazlo tú y pulsa en 'Continuar'.

$$y(x)=C_1x^2+C_2\frac{1}{x}+3x-2 \hspace{1cm} \Rightarrow \hspace{1cm} y(1)=C_1+C_2+1=0 \hspace{1cm} \Rightarrow \hspace{1cm} C_2=-1-C_1$$ Luego las curvas solución que pasan por ese punto forman la siguiente familia uniparamétrica: $$y(x)=C_1x^2-(1+C_1)\frac{1}{x}+3x-2 \hspace{1cm}, \hspace{1.2cm} C_1\in{\bf R}$$

Paso 2

Debemos buscar de entre estas curvas aquellas cuya gráfica tenga pendiente dada en el punto $P(1,0)$. Las diferentes curvas de la familia anterior van resultando de dar diferentes valores a la constante $C_1$. Puesto que hemos de hallar las que tienen una pendiente dada, debemos escribir la constante $C_1$ en función de la pendiente. La pendiente de la gráfica de cada solución en ese punto es

$\frac{y(1)}{1}=0$

$y'(x)$

Ninguna de las opciones presentadas es correcta

Eso no es la derivada de $y$ en $x=1$

Eso es la función derivada.

En efecto, ninguna es correcta. La pendiente es $y'(1)$. Puesto que conocemos $$y(x)=C_1x^2-(1+C_1)\frac{1}{x}+3x-2$$ podemos escribir $C_1$ en función de $y'(1)$. Hazlo tú y pulsa en 'Continuar' cuando lo tengas.

Partiendo de la expresión $y(x)=C_1x^2-(1+C_1)\frac{1}{x}+3x-2$, derivamos y sustituimos $x=1$ en la derivada: $$y'(x)=2C_1x+(1+C_1)\frac{1}{x^2}+3 \hspace{1cm} \Rightarrow \hspace{1cm} y'(1)=3C_1+4 \hspace{1cm} \Rightarrow \hspace{1cm} C_1=\frac{1}{3}(y'(1)-4)$$

Paso 3

Para representar las tres curvas correspondientes a $y'(1)=-1$, $y'(1)=0$ e $y'(1)=1$, una opción es utilizar varias veces el comando plot, agrupándolas en un ciclo for. El esquema podría ser

definir un vector con los valores de la pendiente
utilizarlo para definir un vector con los valores de la constante
definir un vector con los valores de las abscisas
hacer un ciclo 'for' para que dibuje las tres curvas

Piensa cómo seguirías este esquema para dibujar las curvas y pulsa en 'Continuar'.

p=-1:1;
c=(p-4)/3;
x=.5:.05:1.5;
for k=1:3
    plot(x,c(k)*x.^2-(1+c(k))./x+3*x-2)
    hold on
end
    hold off
    axis equal

La salida en la ventana de figuras será

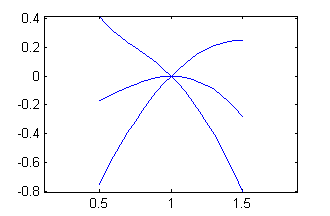
Gráfica

Otra opción para dibujar estas curvas es utilizar el comando 'meshgrid'. Igual que con la opción anterior, empezaremos definiendo los vectores de pendientes, el de la constante y el de abscisas, pero después generaremos una matriz que guarde las ordenadas para los tres valores de la constante y utilizaremos un único 'plot':

p=-1:1;
c=(p-4)/3;
x=.5:.05:1.5;
[X,C]=meshgrid(x,c);
Y=C.*X.^2-(1+C)./X+3*X-2;
plot(x,Y)
axis equal

El resultado es

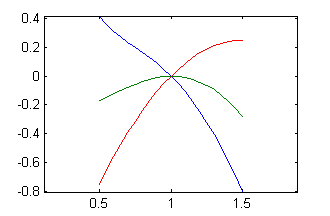
Gráfica

Resolución del tercer apartado

Paso 1

En el apartado anterior se fijó un punto de paso y se encontraron las soluciones que pasaban por él. En éste apartado lo que se fija es la pendiente correspondiente a $x=1$. Derivando la expresión de la familia biparamétrica e imponiendo que esa derivada valga $1/2$ en $x=1$ obtendremos una relación entre las constantes $C_1$ y $C_2$ que podrá utilizarse para escribir una familia que dependa sólo de una constante. Sigue este proceso para encontrar esa familia y pulsa en 'Ver' cuando la tengas.

Ver

$$y(x)=C_1x^2+C_2\frac{1}{x}+3x-2 \hspace{1cm} \Rightarrow \hspace{1cm} y'(x)=2C_1x-C_2\frac{1}{x^2}+3 \hspace{1cm} \Rightarrow \hspace{1cm} y'(1)=2C_1-C_2+3=\frac{1}{2}$$ Podemos despejar $C_2$ en función de $C_1$ y llegar a $$y(x)=C_1x^2+\left(2C_1+\frac{5}{2}\right)\frac{1}{x}+3x-2 \hspace{.6cm}, \hspace{.8cm} C_1\in{\bf R}$$ Obviamente también podría haberse despejado $C_1$ en función de $C_2$ y escribir la familia con la constante $C_2$.

Paso 2

Una vez encontrada la familia de curvas solución que tienen pendiente $1/2$ cuando se cortan con $x=1$ debemos dibujar entre ellas las que pasan por los puntos $P_m(1,m)$ para $m=-3:3$. ¿Cuáles son los valores que debemos dar a la constante $C_1$? Piénsalo y pulsa en 'Ver' cuando lo tengas.

Ver

Sustituyendo $x=1$ en la expresión de la familia calculada antes, tendremos $$y(1)=3C_1+\frac{7}{2}$$ luego $$C_1=\frac{1}{3}\left(m-\frac{7}{2}\right)$$

Paso 3

Para dibujarla en el ordenador utiliza el comando 'meshgrid', siguiendo el esquema de la segunda opción de las seguidas antes. Inténtalo tú y pulsa en 'Continuar' cuando lo tengas.

En este caso escribiremos

m=-3:3;
c=(m-7/2)/3;
x=.5:.05:1.5;
[X,C]=meshgrid(x,c);
Y=C.*X.^2+(2*C+5/2)./X+3*X-2;
plot(x,Y)
axis equal

El resultado es

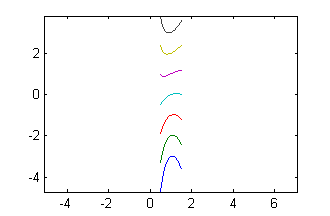
Gráfica

donde puede adivinarse la pendiente $1/2$ en cada una de las curvas a su paso por $x=1$. La desventaja es el reducido tamaño de los arcos. Para verlos un poco más grandes podemos quitar la línea 'axis equal':

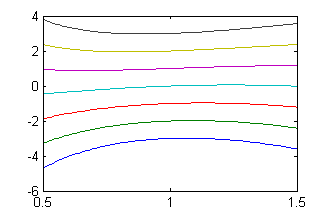
Gráfica

Resolución del cuarto apartado

Paso 1

Sabemos que si $y=y(x)$ tiene un extremo para $x=2$, entonces $y'(2)=0$. Utilizaremos esto para encontrar la familia uniparamétrica de curvas solución que tienen un extremo en $x=2$: $$y(x)=C_1x^2+C_2\frac{1}{x}+3x-2 \hspace{.7cm} \Rightarrow \hspace{.7cm} y'(x)=2C_1x-C_2\frac{1}{x^2}+3 \hspace{.7cm} \Rightarrow \hspace{.7cm} y'(2)=4C_1-\frac{1}{4}C_2+3=0$$ de donde $$y(x)=C_1x^2+4(4C_1+3)\frac{1}{x}+3x-2 \hspace{.6cm}, \hspace{.8cm} C_1\in{\bf R}$$

Paso 2

Para buscar dos curvas solución que tengan un máximo cuando cortan a $x=2$, debemos imponer que la segunda derivada en $x=2$ sea negativa. Hazlo tú y pulsa en 'Ver'.

Ver

$$y(x)=C_1x^2+4(4C_1+3)\frac{1}{x}+3x-2\hspace{.7cm} \Rightarrow \hspace{.7cm} y''(x)=2C_1+8(4C_1+3)\frac{1}{x^3}\hspace{.7cm} \Rightarrow \hspace{.7cm} y''(2)=3(2C_1+1)$$ Luego la segunda derivada en $x=2$ es negativa si $C_1<-1/2$. Podemos tomar para $C_1$ dos valores en ese rango, por ejemplo $C_1=-3/2$ y $C_1=-1$. Las representamos con

c=[-3/2 -1];
x=1.5:.001:2.5;
[X,C]=meshgrid(x,c);
Y=C.*X.^2+4*(4*C+3)./X+3*X-2;
plot(x,Y)

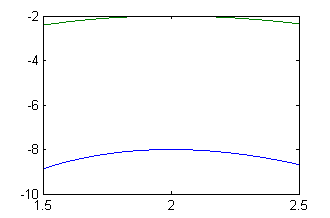
Gráfica

Paso 3

Debemos buscar ahora dos curvas solución que tengan un mínimo cuando cortan a $x=2$. En base al cálculo realizado antes sabemos que debemos tomar dos valores de $C_1$ mayores que $-1/2$. Por ejemplo, dibujaremos las curvas correspondientes a $C_1=0$ y $C_1=1/2$. Escribe las líneas para el ordenador con las que dibujas estas curvas. Pulsa en 'Ver' cuando lo tengas.

Ver

c=[0 1/2];
x=1.5:.001:2.5;
[X,C]=meshgrid(x,c);
Y=C.*X.^2+4*(4*C+3)./X+3*X-2;
plot(x,Y)

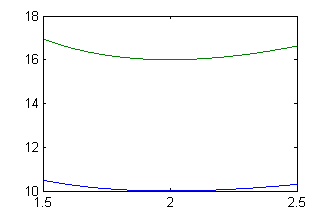
Gráfica

Paso 4

Se pide ahora que el valor del mínimo esté entre 5 y 10. El valor del mínimo es $y(2)$. Puesto que $$y(x)=C_1x^2+4(4C_1+3)\frac{1}{x}+3x-2$$ sabemos que $$y(2)=12C_1+10$$ luego debemos tomar un valor de $C_1$ cumpliendo $$5<12C_1+10<10 $$ que es lo mismo que $$-\frac{5}{12}<C_1<0$$ Por ejemplo, con $C_1=-1/4$, resulta la función $$y(x)=-\frac{x^2}{4}+\frac{8}{x}+3x-2$$ que representamos en rojo junto con las dos anteriores

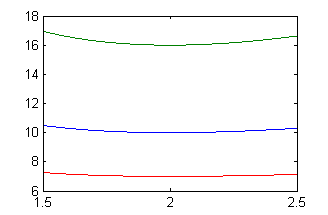
Gráfica

c=[0 1/2 -1/4];
x=1.5:.001:2.5;
[X,C]=meshgrid(x,c);
Y=C.*X.^2+4*(4*C+3)./X+3*X-2;
plot(x,Y)

Aunque no se pida en el ejercicio podríamos analizar también la curva, de entre las que tienen derivada nula en $x=2$, correspondiente a $C_1=-1/2$: $$y(x)=-\frac{x^2}{2}+\frac{4}{x}+3x-2$$ Para esta curva es nula la segunda derivada en $x=2$ pero no la tercera, así que tiene un punto de inflexión en $x=2$:

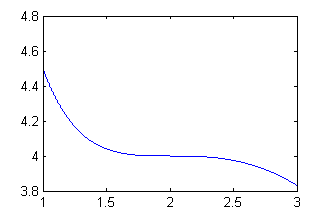
Gráfica

x=1:.001:3;
y=-x.^2/2+4./x+3*x-2;
plot(x,y)

Resumen

En el primer apartado se encuentra la ecuación cuya solución general es la familia dada. Este es un apartado que no se utilizará en la resolución de los posteriores, pues en el resto del ejercicio se trabajará con la forma de la familia solución general, no con la ecuación.
Fijado un punto de paso se encuentra la familia uniparamétrica de soluciones que pasan por ese punto. Se concretan tres pendientes y se representan en el ordenador las correspondientes curvas.
Se encuentra la familia uniparamétrica de soluciones con una pendiente dada en los cortes de las soluciones con un eje vertical dado. De entre éstas se representan en el ordenador las que pasan por siete puntos dados.
Se determina la familia de soluciones que tienen un extremo en sus cortes con un eje vertical dado y de entre ellas se piden dos con máximo, dos con mímino y una con un mínimo acotado entre dos valores.

Índice de tema