Enunciado
Dos depósitos, que llamaremos 1 y 2, están concectados de manera que del 1 pasa al 2 un volumen de 4 litros por minuto y del 2 pasa al 1 un volumen de 3 litros por minuto. Al depósito 1 está entrando una disolución a razón de 5 litros por minuto con $0.1$ Kg. de soluto por litro. Inicialmente en el depósito 1 la cantidad de soluto es de 4 Kg. y en el 2 es de 5 Kg. Los volúmenes iniciales son $V_{10}=40$ litros y $V_{20}=100$ litros.
- Caso 1: No hay salida de disolución hacia fuera del sistema.
- Escribe el sistema diferencial que modela las cantidades de soluto en los depósitos.
- Halla las expresiones de esas cantidades de soluto en función del tiempo.
- Representa las gráficas de esas funciones para $t$ entre 0 y 10 minutos.
- Compara los resultados obtenidos con el comando 'ode45', para un paso de $t$ de una décima de minuto.
- Caso 2: El depósito 2 tiene un orificio de salida.
- Escribe el sistema diferencial que modela las cantidades de soluto en los depósitos si la disolución sale a razón de 2 litros por minuto. Utiliza un método numérico para estimar las cantidades de soluto para $t$ entre 0 y 10 minutos. Representa esas estimaciones.
- Repite el apartado anterior si la razón de salida es de 5 litros por minuto.
- Escribe el sistema diferencial que modela las cantidades de soluto en los depósitos.
- Halla las expresiones de esas cantidades de soluto en función del tiempo.
- Representa las gráficas de esas funciones para $t$ entre 0 y 10 minutos.
- Compara los resultados obtenidos con el comando 'ode45', para un paso de $t$ de una décima de minuto.
- Escribe el sistema diferencial que modela las cantidades de soluto en los depósitos si la disolución sale a razón de 2 litros por minuto. Utiliza un método numérico para estimar las cantidades de soluto para $t$ entre 0 y 10 minutos. Representa esas estimaciones.
- Repite el apartado anterior si la razón de salida es de 5 litros por minuto.
Resolución del primer apartado del Caso 1
Lo primero que hemos de analizar es cómo cambian los volúmenes en cada depósito. Podemos recoger la información del enunciado en una tabla:
De aquí deducimos que los volúmenes de disolución en los depósitos no son constantes. Dependen de $t$, en minutos, según las fórmulas... Encuéntralas y pulsa en 'Ver'.
| entran (por minuto) | salen (por minuto) | |
| Depósito 1 | $5+3$ litros | 4 litros |
| Depósito 2 | 4 litros | 3 litros |
Ver
Cada minuto se acumulan 4 litros en el depósito 1 y 1 litro en el 2, luego
$$V_1(t)=V_{10}+4t=4(10+t) \hspace{.5cm} , \hspace{.5cm} V_2(t)=V_{20}+t=100+t$$
Llamamos $S_1(t)$ y $S_2(t)$ a las cantidades (en Kg.) de soluto en los depósitos 1 y 2 respectivamente, en función del tiempo en minutos.
Debemos escribir las ecuaciones diferenciales para $S_1(t)$ y $S_2(t)$. Para ello utilizamos que la tasa de acumulación de soluto en cada depósito es la diferencia entre la tasa de entrada y la tasa de salida; cada una de estas tasas se mide, en este problema, en Kg$/$minuto. La primera ecuación es:
$$S'_1(t)=3\frac{S_2(t)}{V_2(t)}-4\frac{S_1(t)}{V_1(t)}$$
$$S'_1(t)=-4\frac{S_2(t)}{V_2(t)}+3\frac{S_1(t)}{V_1(t)}$$
Ninguna de las propuestas es correcta.
No estás teniendo en cuenta la entrada de disolución al depósito desde el exterior.
Revisa, está completamente mal.
En efecto, ninguna de las dos propuestas es correcta; en la más acertada falta el término debido a la entrada de disolución desde el exterior al depósito 1. Escribe la correcta y también la correspondiente a $S'_2(t)$, junto con las condiciones iniciales y pulsa en 'Continuar'
El sistema completo es
$$\left\{\begin{array}{ll}
S'_1(t)=0.5+3\frac{S_2(t)}{V_2(t)}-4\frac{S_1(t)}{V_1(t)} , & S_1(0)=4 \\
S'_2(t)=4\frac{S_1(t)}{V_1(t)}-3\frac{S_2(t)}{V_2(t)} , & S_2(0)=5
\end{array}\right.$$
Resolución del segundo apartado del Caso 1
Este sistema admite una resolución analítica sencilla, pues si sumamos las dos ecuaciones tendremos $$S'_1(t)+S'_2(t)=0.5$$ expresión que podemos integrar: $$S_1(t)+S_2(t)=\frac{t}{2}+C$$ ¿Qué podemos hacer para calcular el valor de la constante $C$? Piénsalo y pulsa en 'Ver' cuando lo tengas.
Ver
La expresión es válida en todos los valores de $t$, luego también para $t=0$:
$$S_1(0)+S_2(0)=C \hspace{.5cm} \Rightarrow \hspace{.5cm} C=9$$
con lo cual
$$S_1(t)=\frac{t}{2}+9-S_2(t)$$
Sustituyendo esta expresión en la segunda ecuación del sistema,
$$S'_2(t)+\left(\frac{4}{V_1(t)}+\frac{3}{V_2(t)}\right)S_2(t)=\frac{4}{V_1(t)}\left(\frac{t}{2}+9\right)$$
y sustituyendo las expresiones de $V_1(t)$ y de $V_2(t)$, obtenemos
$$S'_2(t)+\left(\frac{1}{10+t}+\frac{3}{100+t}\right)S_2(t)=\frac{t+18}{2(10+t)}$$
que es una ecuación de primer orden lineal. Encuentra su solución general y pulsa en 'Continuar'.
Si llamamos $$p(t)=\frac{1}{10+t}+\frac{3}{100+t}$$ el factor integrante es
$$\mu(t)=e^{\int p(t)\, dt}$$
es decir,
$$\mu(t)=(10+t)(100+t)^3$$
y la solución general es
$$S_2(t)=\frac{1}{2(10+t)(100+t)^3}\int (18+t)(100+t)^3\, dt$$
Para ahorrarnos trabajo en el cálculo de esta primitiva podemos recurrir al ordenador,
$$q(t)=\int (18+t)(100+t)^3\, dt=\frac{t^5}{5}+\frac{159 t^4}{2}+11800 t^3+77\cdot 10^4 t^2+18\cdot 10^6 t+C$$
y entonces
$$S_2(t)=\frac{q(t)}{2(10+t)(100+t)^3}$$
El valor de la constante $C$ se obtiene imponiendo que $S_2(0)=5$:
$$S_2(0)=5=\frac{C}{2\cdot 10^7}\hspace{.5cm} \Rightarrow \hspace{.5cm} C=10^8$$
La expresión para $S_1(t)$ se obtendrá de
$$S_1(t)=\frac{t}{2}+9-S_2(t)$$
Resolución del tercer apartado del Caso 1
Si para calcular la primitiva precisa para determinar $S_2(t)$ habíamos utilizado el ordenador, podemos añadir en el mismo fichero las líneas para definir $S_1(t)$ y $S_2(t)$ como objetos simbólicos y a continuación generar con ellos vectores que representar con el 'plot':
%%%%%%% cálculo de las expresiones simbólicas para S_1 y S_2
syms t;
q=int((t+18)*(100+t)^3);
s2=(q+10^8)/(2*(10+t)*(100+t)^3); % cantidad en el dep.2
s1=t/2+9-s2; % cantidad en el dep.1
%%%%%% representación
vt=0:.1:10;
vs1=subs(s1,t,vt); % cantidades en el dep. 1 para t entre 0 y 10 cad décima de min.
vs2=subs(s2,t,vt); % cantidades en el dep. 2 para t entre 0 y 10 cad décima de min.
vs=[vs1' vs2']
figure(1)
plot(vt,vs)
xlabel('tiempo (min)');ylabel('cantidades de soluto (Kg)')
legend('depósito 1','depósito 2','Location','North')
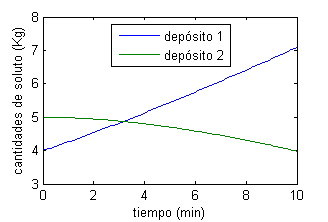
La ejecución de estas líneas produce en la figura 1 las siguientes gráficas:
Resolución del cuarto apartado del Caso 1
Utilizamos ahora 'ode45' como en otras ocasiones, definiendo previamente una función vectorial con los segundos miembros de las ecuaciones. Añadiremos en el fichero anterior las siguientes líneas%%%%%%%% aproximación con ode45 y comparación f=@(u,s) [.5+3*s(2)/(100+u)-s(1)/(10+u);-3*s(2)/(100+u)+s(1)/(10+u)]; [vt,sest]=ode45(f,vt,[4 5]); difer=sest-vsTras ejecutarlo podemos comprobar que la aproximación es muy buena, pues la diferencia entre los valores más distantes es de $6\cdot 10^{-8}$.
Resolución del primer apartado del Caso 2
A los mismos datos del apartado anterior se añade la salida de disolución del depósito 2, a razón de 2 litros por minuto. Ahora la tabla de entrada y salida es la siguiente:
| entran (por minuto) | salen (por minuto) | |
| Depósito 1 | $5+3$ litros | 4 litros |
| Depósito 2 | 4 litros | $3+2$ litros |
Ver
El sistema es
$$\left\{\begin{array}{ll}
S'_1(t)=0.5+3\frac{S_2(t)}{V_2(t)}-4\frac{S_1(t)}{V_1(t)} , & S_1(0)=4 \\
S'_2(t)=4\frac{S_1(t)}{V_1(t)}-5\frac{S_2(t)}{V_2(t)} , & S_2(0)=5
\end{array}\right.$$
o bien
$$\left\{\begin{array}{ll}
S'_1(t)=0.5+3\frac{S_2(t)}{100-t}-\frac{S_1(t)}{10+t} , & S_1(0)=4 \\
S'_2(t)=\frac{S_1(t)}{10+t}-5\frac{S_2(t)}{100-t} , & S_2(0)=5
\end{array}\right.$$
Para estimar las cantidades de soluto $S_1(t)$ y $S_2(t)$, podemos recurrir de nuevo a 'ode45' y representar los valores obtenidos frente al tiempo. Escribe cómo harías esos cálculos y representarías las aproximaciones en la figura 2. Pulsa en 'Continuar' cuando lo termines.
%%%%%%%%%%%%%% aproximación con ode45 cuando se abre orificio de salida en
%%%%%%%%%%%%%% dep 2, con flujo de salida= 2
f=@(u,s) [.5+3*s(2)/(100-u)-s(1)/(10+u);-5*s(2)/(100-u)+s(1)/(10+u)];
[vt,sest]=ode45(f,vt,[4 5]);
figure(2)
plot(vt,sest)
xlabel('tiempo (min)');ylabel('cantidades de soluto (Kg)')
legend('depósito 1','depósito 2','Location','North')
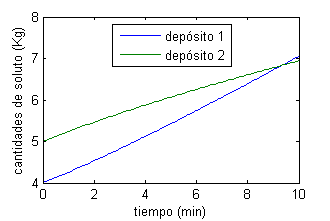
Las gráficas de las cantidades aproximadas son
Resolución del segundo apartado del Caso 2
En este apartado la razón de salida es de 5 litros por minuto:
| entran (por minuto) | salen (por minuto) | |
| Depósito 1 | $5+3$ litros | 4 litros |
| Depósito 2 | 4 litros | $3+5$ litros |
Ver
%%%%%%%%%%%%%% aproximación con ode45 cuando se abre orificio de salida en
%%%%%%%%%%%%%% dep 2, con flujo de salida= 5
f=@(u,s) [.5+3*s(2)/(100-4*u)-s(1)/(10+u);-2*s(2)/(25-u)+s(1)/(10+u)];
[vt,sest]=ode45(f,vt,[4 5]);
figure(3)
plot(vt,sest)
xlabel('tiempo (min)');ylabel('cantidades de soluto (Kg)')
legend('depósito 1','depósito 2','Location','North')
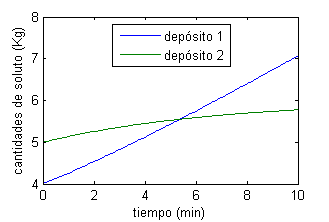
Las gráficas de las cantidades aproximadas son