Índice de tema

 

Enunciado

Supongamos que un cuerpo de masa $m=0.5$ Kg está cayendo en un medio que opone una resistencia proporcional al cuadrado de la velocidad; la constante de proporcionalidad depende de la forma del objeto y del medio que se trate y se medirá en Kg$/$m; tomaremos como aceleración de la gravedad $g=9.81 $m$/$s$^2$. Inicialmente el cuerpo se deja caer sin velocidad inicial.
  1. Encuentra el problema de valor inicial que modeliza este proceso.
  2. Halla y representa gráficamente los valores del desplazamiento y la velocidad del cuerpo durante los primeros dos segundos, cada décima de segundo, tomando como constante de proporcionalidad $K=2$ Kg$/$m.
  3. Analiza cómo se modifican los resultados anteriores si se duplica el valor de la constante de proporcionalidad.

Resolución del primer apartado

Un problema de valor inicial está formado por una ecuación diferencial y los valores de la solución en cierto valor de la variable independiente. En este problema
  • la variable independiente es el tiempo, $t$, medido en segundos
  • la variable dependiente es el desplazamiento desde la situación de reposo incial, $s$, medido en metros
  • el desplazamiento inicial (para $t=0$) es cero
  • la velocidad inicial (para $t=0$) es cero
  • la aceleración del cuerpo es la diferencia entre la aceleración de la gravedad (que ayuda al movimiento) y la aceleración en sentido opuesto provocada por la resistencia del medio
Este último punto nos lleva a establecer como ecuación diferencial para $s(t)$ la siguiente:
Ninguna de las propuestas es correcta
$$\frac{d^2s}{dt^2}=g-K\left(\frac{ds}{dt}\right)^2$$
$$\frac{d^2s}{dt^2}=g-\frac{K}{m}\left(\frac{ds}{dt}\right)^2$$
Fíjate bien, una de las dos propuestas es correcta.
Todos los términos de la ecuación deben expresenarse en las mismas unidades: $\frac{d^2s}{dt^2}$ y $g$ son aceleraciones, pero $K\left(\frac{ds}{dt}\right)^2$ es una fuerza.
En efecto, eso es lo correcto: $K\left(\frac{ds}{dt}\right)^2$ es la fuerza de resistencia que ejerce el medio sobre el cuerpo, luego el término $\frac{K}{m}\left(\frac{ds}{dt}\right)^2$ será la aceleración que hemos de restar a la de la gravedad. Por tanto el problema de valor inicial es $$\frac{d^2s}{dt^2}=g-\frac{K}{m}\left(\frac{ds}{dt}\right)^2 \hspace{.5cm} , \hspace{.5cm} s(0)=0 \hspace{.5cm} , \hspace{.5cm} s'(0)=0$$

Resolución del segundo apartado

Utilizaremos el comando 'ode45' para realizar la aproximación de $s(t)$ y de $s'(t)$ en los valores de $t$ comprendidos entre $t=0$ y $t=2$ cada décima de segundo y después se representarán las estimaciones en la misma gráfica. Para ello debemos primero escribir el sistema diferencial de dos ecuaciones de primer orden equivalente a nuestro problema de valor inicial. Hazlo tú y pulsa en 'Ver'
Ver
El sistema diferencial es $$\left\{\begin{array}{lll}x'_1(t)=x_2(t) & , & x_1(0)=0 \\ x'_2(t)=g-\frac{k}{m}x_2(t)^2 & , & x_2(0)=0 \end{array}\right.$$ En las líneas de código que escribamos para el ordenador, podemos seguir el siguiente orden
  1. Asignar valores a los parámentros del problema, (los dejaremos con su nombre en las ecuaciones, para que la escritura sea más clara)
  2. Definir la función vectorial con los segundos miembros de las ecuaciones del sistema
  3. Hallar las aproximaciones de $x_1$ y de $x_2$ (que son $s$ y $s'$) con 'ode45'
  4. Dibujar las aproximaciones en una misma figura
  5. Poner nombre al eje temporal y añadir una leyenda.
Intenta escribir este código y pulsa en 'Continuar'.
Ejecutando 
g=9.81; %% valor de la constante de la gravedad
m=.5;   %% masa del cuerpo
k=2;    %% constante de resistencia del medio
f=@(t,x) [x(2); g-k*x(2)^2/m]  %% funciones del sistema
[t,xest]=ode45(f,0:.1:2,[0 0])   %% cálculo de la aproxiamción
plot(t,xest)                     %% dibujo de las estimaciones
xlabel('tiempo (s)')             %% etiqueta para el eje horizontal
legend('desplazamiento (m)','velocidad (m/s)','Location','North')  %% leyenda
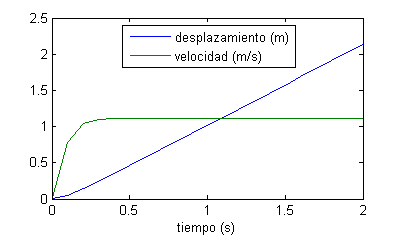
obtendremos en la ventana de comandos el valor de las aproximaciones y en la ventana de dibujo la figura

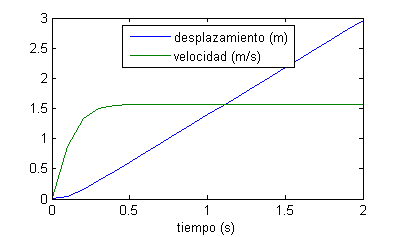
Gráfica

Podemos observar cómo la velocidad tiende a estacionarse, tendiendo al valor en que $s''(t)=0$. Teniendo en cuenta la ecuación diferencial que verifica $s$, la velocidad tiende a ... Piénsalo y pulsa en 'Continuar'.
Si en la ecuación hacemos $s''=0$, para el valor de $t$ correspondiente (sea $t_f$) deberá cumplir, $$\left(\frac{ds}{dt}\right)^2(t_f)=g\frac{m}{k}$$ es decir, $$\frac{ds}{dt}(t_f)=\sqrt{g\frac{m}{k}}=1.5660$$ La gráfica del desplazamiento tiende por tanto a ser una recta de pendiente $=1.5660$.

Resolución del tercer apartado

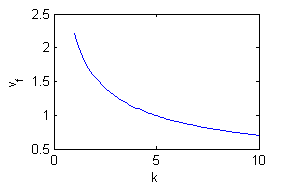
Debemos repetir el apartado anterior, únicamente hemos de modificar el valor de la constante $k$. Las gráficas en este caso son

Gráfica

El valor al que tiende la velocidad es ahora $$\frac{ds}{dt}(t_f)=\sqrt{g\frac{m}{k}}=1.1074$$ Obviamente este valor al que tiende la velocidad del cuerpo es decreciente para valores crecientes de $k$; si llamamos $v_f$ al valor límite de la velocidad, la gráfica de $v_f$ frente a $k$ es decreciente y cóncava hacia arriba, pues es $v_f=\sqrt{g\frac{m}{k}}$:

Gráfica

lo que significa que a medida que crece $k$, cuesta más que el valor límite de la velocidad disminuya.