Ejercicios preliminares e instantáneos. Ecuaciones diferenciales ordinarias segundo orden.

Ejercicio 1

Analiza cuáles de las siguientes funciones son soluciones de la ecuación diferencial $$x^2y''-3xy'+3y=3x^4-x^2\log x$$
  1. $y_1(x)=x-x^3+x^4+x^2\log x$
  2. $y_2(x)=-y_1(x)$
  3. $y_3(x)=-x+x^3+x^4+x^2\log x$
  4. $y_4(x)=2x-x^3+x^4+x^2\log x$
Pista
Solución
Puedes comprobar cada una independientemente, derivando y sustituyendo en la ecuación. Pero también puedes utilizar la relación existente entre ellas.
Todas son soluciones salvo la $y_2(x)$.

Ejercicio 2

¿Cuáles de las siguientes ecuaciones son lineales?:
  1. $\frac{d^2T}{dz^2}-\frac{1}{z}\frac{dT}{dz}=T$
  2. $y''-yy'=x$
  3. $\frac{d^2C}{dt^2}+3tC=t^2$
  4. $\frac{d^2T}{dz^2}-\frac{1}{z}\frac{dT}{dz}=T^2$
  5. $\frac{d^2C}{dt^2}+\frac{1}{C}\frac{dC}{dt}=0$
Pista
Solución
Para que una ecuación de segundo orden sea lineal ha de poderse escribir de la forma: $$a(t)y''(t)+b(t)y'(t)+c(t)y(t)=f(t)$$
Son lineales las ecuaciones de los apartados a) y c).

Ejercicio 3

¿Cuáles de las siguientes familias de funciones pueden ser solución general de una e.d.o. lineal de segundo orden homogénea?
  1. $y(x)=C_1x+C_2e^{-2x}$
  2. $y(x)=C_1+C_2e^{-x}+e^{2x}$
  3. $y(x)=C_1+C_2e^{3x}+C_3x$
  4. $y(x)=C_1x+\frac{C_2}{x}$
  5. $y(x)=C_1\frac{1}{x}\cos x+C_2\frac{1}{x}\mbox{sen}\, x$
  6. $y(x)=C_1e^{-x}+\frac{C_2}{e^x}$
Pista
Solución
La solución general de una e.d.o. lineal de segundo orden homogénea es una familia biparamétrica de funciones, generada como combinación lineal $$C_1y_1(x)+C_2y_2(x)$$ de dos soluciones $y_1(x)$ e $y_2(x)$ linealmente independientes. Para resolver este ejercicio también podemos utilizar que la combinación lineal de soluciones de una ecuación lineal homogénea debe ser así mismo solución de la ecuación.
  1. Sí puede serlo.
  2. No puede serlo, por el factor $e^{2x}$.
  3. No puede serlo, pues se trata de una familia dependiente de tres parámetros.
  4. Sí puede serlo.
  5. Sí puede serlo.
  6. No, pues es una familia uniparamétrica.

Ejercicio 4

Determina de cuál de las siguientes ecuaciones es solución particular la función $$y=\cos x-\mbox{sen}\, x+2x\cos x$$
  1. $y''-y'+2y=4x\cos x-2\,\mbox{sen}\, x$
  2. $y''+y=-4\,\mbox{sen}\, x$
  3. $y''+y=0$
Pista
Solución
Sólo tienes que derivar y sustituir.
La función $y=\cos x-\mbox{sen}\, x+2x\cos x$ es solución de la ecuación del apartado b)

Ejercicio 5

Clasifica como problema de valor inicial (p.v.i), problema de valores en la frontera (p.v.f) o problema mixto cada uno de los siguientes
  1. $y''-xy'+y=x^2$, $y(0)=0$, $y(1)=-1$
  2. $y''-y'+y/x=x^2$, $y(1)=0$, $y'(1)=-1$
  3. $y''-y'+y=x$, $y(0)=y'(0)$, $y(1)=0$
  4. $y''-y'+y=x$, $y(0)=y'(0)$, $y(1)+y'(1)=0$
Pista
Solución
Un problema de valor inicial está formado por la ecuación diferencial y los valores de la función incógnita en un valor de $x$ dado; se trata de un problema de valores en la frontera si lo que se conoce es el valor de la incógnita en los extremos de un intervalo; el problema es mixto si la ecuación se acompaña de datos de la forma $$a_1y(a)+a_2y'(a)=y_0\ ,\ \ b_1y(b)+b_2y'(b)=y_1$$ siendo $a$ y $b$ los extremos del intervalo en el que se considera la ecuación.
  1. es un p.v.f;
  2. es un p.v.i;
  3. es un problema mixto;
  4. es un problema mixto.

Ejercicio 6

¿Por qué punto y con qué pendiente corta al eje $x=0$ la gráfica de cada una de las siguientes funciones?
  1. $y=2e^x+xe^{-x}$
  2. $y=x(\cos x-\mbox{sen}\, x)$
  3. $y=e^{3x}(C_1+C_2x)$
  4. $y=e^{-x}(C_1\cos x+C_2\,\mbox{sen}\, x)$
Pista
Solución
Obviamente, la gráfica de la función $y=y(x)$ corta al eje $x=0$ en el punto $(0,y(0))$, siendo la pendiente de la gráfica en ese punto igual a $y'(0)$.
  1. $y=2e^x+xe^{-x}$ corta al eje $x=0$ en el punto $P(0,2)$, con pendiente $y'(0)=3$:
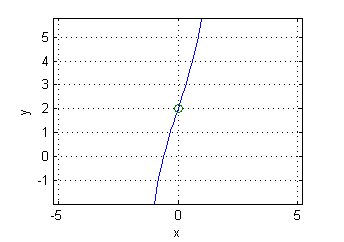
    Gráfica 
    x=-1:.1:1;
plot(x,2*exp(x)+x.*exp(-x),0,2,'o')
grid on
axis equal
xlabel('x');ylabel('y');
  2. $y=x(\cos x-\mbox{sen}\, x)$ corta al eje $x=0$ en el punto $P(0,0)$, con pendiente $y'(0)=1$:
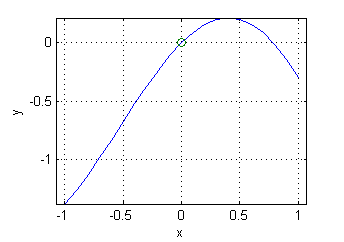
    Gráfica 
    x=-1:.1:1;
plot(x,x.*(cos(x)-sin(x)),0,0,'o')
grid on
axis equal
xlabel('x');ylabel('y');
  3. Cada una de las gráficas de las funciones de la forma $y=e^{3x}(C_1+C_2x)$ corta al eje $x=0$ en el punto $P(0,C_1)$, pendiente $3C_1+C_2$. Por ejemplo, puedes ver las gráficas entre $x=-0.2$ y $x=0.2$ de las siete funciones correspondientes a $C_2=0.6$ y a $C_1$ entre $-0.3$ y $0.3$ con paso $0.1$:
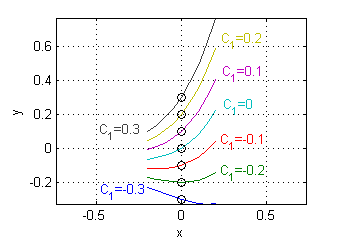
    Gráfica
    La pendiente en cada punto de corte con el eje $x=0$ es $3C_1+0.6$ 
      x=-.2:.05:.2;
  [X,C1]=meshgrid(x,-.3:.1:.3);
  Y=exp(3*X).*(C1+.6*X);
  plot(x,Y)
  hold on
  plot(zeros(1,7),-.3:.1:.3,'ok')
  hold off
  grid on
  axis equal
  xlabel('x');ylabel('y');
  4. Cada una de las gráficas de las funciones de la forma $y=e^{-x}(C_1\cos x+C_2\,\mbox{sen}\, x)$ corta al eje $x=0$ en el punto $P(0,C_1)$, con pendiente $C_2-C_1$. Por ejemplo, puedes ver las gráficas entre $x=-1$ y $x=1$ de las seis funciones correspondientes a $C_2=1$ y a $C_1$ entre $-1$ y $1$ con paso $0.4$:
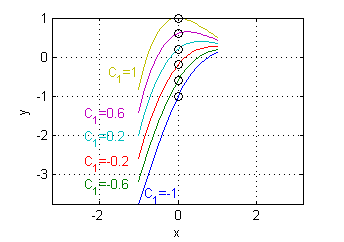
    Gráfica
    La pendiente en cada punto de corte con el eje $x=0$ es $1-C_1$ 
    x=-1:.05:1;
[X,C1]=meshgrid(x,-1:.4:1);
Y=exp(-X).*(C1.*cos(X)+sin(X));
plot(x,Y)
hold on
plot(zeros(1,6),-1:.4:1,'ok')
hold off
grid on
axis equal
xlabel('x');ylabel('y');

Ejercicio 7

Verdadero o falso: hay dos funciones $y=y(x)$ distintas, definidas en el intervalo $(-1,1)$, que cortan al eje $x=0$ en el mismo punto y con la misma pendiente y que cumplen que $y''-y'\,\mbox{sen}\, x+y=x$.
Pista
Solución
Debes utilizar el teorema de existencia y unicidad de solución para un problema de tipo $$y''+p(x)y'+q(x)y=g(x)\ ,\ \ y(x_0)=y_0\ ,\ \ y'(x_0)=y_1$$ Este teorema establece que la continuidad de las funciones $p(x)$, $q(x)$ y $g(x)$ en un intervalo $(a,b)$, que contiene a $x_0$, garantiza que el problema anterior tiene solución única en ese intervalo.
El enunciado es falso, pues este problema cumple el teorema de existencia y unicidad de solución: Si dos soluciones pasaran por el mismo punto $(0,y_0)$ con las misma pendiente, significaría que cumplen las mismas condiciones para $x=0$ y eso no puede ocurrir en base a la unicidad de solución del problema $$y''-y'\,\mbox{sen}\, x +y=x\ ,\ \ y(0)=y_0\ ,\ \ y'(0)=y_1$$

Ejercicio 8

  1. ¿Pueden ser $y_1(x)=e^{-x}$, $y_2(x)=e^x$ e $y_3(x)=e^{2x}$ soluciones de la misma e.d.o. lineal de segundo orden homogénea?
  2. ¿Pueden serlo $y_1(x)=\cos x$, $y_2(x)=\cos 2x$ e $y_3(x)=\cos 3x$?
  3. ¿Cuántas funciones que no sean combinación lineal unas de otras pueden ser soluciones de la misma e.d.o. lineal de segundo orden homogénea?
Solución
  1. No, pues forman un sistema de funciones linealmente independiente: ninguna de las tres puede escribirse como combinación lineal de las otras dos.
  2. No, por la misma razón del apartado anterior.
  3. Dos, por ser éste el orden de la ecuación diferencial.

Ejercicio 9

  1. ¿Puede ser $y=xe^{2x}$ solución de una e.d.o. lineal de segundo orden homogénea de coeficientes constantes?
  2. ¿Puede serlo $y=x^2e^{2x}$?
  3. ¿Puede ser $y=\log x$ solución de una e.d.o. lineal de segundo orden homogénea?¿Y si es de coeficientes constantes?
Pista
Solución
Ten en cuenta cómo se construye la solución general de una e.d.o. lineal de segundo orden homogénea de coeficientes constantes.
  1. $y=xe^{2x}$ es solución de una e.d.o. lineal de segundo orden homogénea de coeficientes constantes en el caso en que $r=2$ sea raíz doble de la ecuación característica.
  2. $y=x^2e^{2x}$ no puede serlo. Lo sería de una ecuación de tercer orden, en el caso en que $r=2$ fuera raíz triple de su ecuación característica.
  3. $y=\log x$ puede ser solución de una e.d.o. lineal de segundo orden homogénea, pero únicamente si no es de coeficientes constantes.

Ejercicio 10

¿Podemos escribir la ecuación característica de una e.d.o. lineal homogénea de coeficientes no constantes?
Solución
No. La ecuación característica se escribe únicamente para las ecuaciones de coeficientes constantes.

Ejercicio 11

Si los números $p$ y $q$ cumplen que $p^2<4q$,
  1. ¿cuál es la parte imaginaria de las raíces de la ecuación $r^2+pr+q=0$?
  2. ¿cuál es la solución general de la ecuación $y''+py'+qy=0$?
Pista
Solución
Ten en cuenta cómo se construye la solución general de una e.d.o. lineal de segundo orden homogénea de coeficientes constantes.
Si $p^2<4q$ la parte imaginaria de las raíces de la ecuación $r^2+pr+q=0$ es $$\frac{1}{2}\sqrt{4q-p^2}$$ La ecuación característica asociada a $y''+py'+qy=0$ es $r^2+pr+q=0$ luego la solución general de $y''+py'+qy=0$ en caso de que $p^2<4q$ es $$y=e^{-p x/2}\left[C_1\cos\left(\frac{x}{2}\sqrt{4q-p^2}\right)+C_2\,\mbox{sen}\left(\frac{x}{2}\sqrt{4q-p^2}\right)\right]$$

Ejercicio 12

¿Cuál de los siguientes p.v.i. es equivalente al sistema de ecuaciones siguiente? $$\left\{\begin{array}{ll} x'_1(t)=x_2(t) & x_1(0)=1 \\ x'_2(t)=t-x_1(t)+2tx_2(t) & x_2(0)=-1 \end{array}\right.$$
  1. $y''-2ty'+y=t$, $y(0)=1$, $y'(0)=-1$
  2. $y''+2ty'-y=t$, $y(0)=1$, $y'(0)=-1$
Pista
Solución
Llama $y=x_1$
De la primera ecuación del sistema, $$x'_1=y'=x_2\hspace{1cm} \mbox{y} \hspace{1.2cm} x'_2=y''$$ Escribiendo la segunda ecuación en términos de $y$, $y'$ e $y''$ obtenemos la ecuación del apartado a).

Ejercicio 13

Explica si es verdadero o falso:
  1. El método de diferencias finitas permite aproximar la solución de un p.v.f. porque reduce el orden de la ecuación.
  2. El método de diferencias finitas permite hallar la solución de un p.v.f. de forma exacta.
Solución
Las dos afirmaciones son falsas. El método de diferencias finitas permite aproximar (no calcular de forma exacta) los valores que toma la solución de un p.v.f. sobre un conjunto finito de puntos; esta aproximación se realiza a través de un sistema de ecuaciones algebraico (no se reduce el orden de la ecuación).

Ejercicio 14

Selecciona de entre las siguientes las expresiones que son dimensionalmente correctas, si $Q_i$ son masas, $C_0$ es una concentración (Masa/Volumen), $t$ es tiempo, $F_i$ son flujos (Volumen/Tiempo) y $V_i$ son volúmenes:
  1. $\frac{dQ_1}{dt}=-F_1V_1Q_1+F_2V_2Q_2+F_3C_0$
  2. $\frac{dQ_1}{dt}=-\frac{F_1}{V_1}Q_1+\frac{F_2}{V_2}Q_2+F_3C_0$
  3. $dQ_1=-\frac{F_1}{V_1}Q_1+\frac{F_2}{V_2}Q_2+F_3C_0\, dt$
  4. $dQ_1=(-\frac{F_1}{V_1}Q_1+\frac{F_2}{V_2}Q_2+F_3C_0)\, dt$
  5. $dQ_1=(-\frac{Q_1}{V_1}+\frac{Q_2}{V_2}+(F_3+F_2-F_1)C_0)\, dt$
Solución
Sólo son dimensionalmente correctas las expresiones b) y d).