Disolución de la sal de una sustancia

Enunciado

Una sustancia indisoluble contiene en sus poros 5 kilos de sal. Para eliminar esa sal se sumerge la sustancia en 60 litros de agua limpia y se observa que durante 1 hora se disuelve la mitad de la sal. La velocidad de disolución es proporcional a la cantidad de sal no disuelta y a la diferencia entre la concentración en el instante dado y la concentración de la disolución saturada (1 kilo para 3 litros). (El factor de proporcionalidad es constante siempre que las condiciones en las que se está produciendo la disolución no varíen, pero no depende del volumen utilizado)

Traza una gráfica de la cantidad de sal disuelta frente al tiempo en esa primera hora.

¿Cuánta sal se disolvería en el mismo tiempo si se hubiera utilizado el doble de agua?

Traza una gráfica de la cantidad de sal disuelta en 1 hora respecto del volumen de agua utilizado, tomando ese volumen entre 60 y 300 litros.

Resolución del primer apartado

Para trazar esa gráfica hemos de conocer la cantidad de sal disuelta respecto del tiempo. Para hallar esta cantidad debemos dar los pasos que se presentan a continuación desordenados:

A) encontrar la solución general de la ecuación
B) si en la ecuación hay un parámetro (por ejemplo en este caso tendremos la constante de proporcionalidad), determinarlo con el dato que proporciona el enunciado
C) establecer los nombres de las variables y constantes del problema
D) escribir el problema de valor inicial (ecuación + condición inicial) que verifica la cantidad de sal disuelta
E) imponer la condición particular

El orden que debemos seguir es

C), D), E), A), B)

C), B), D), E), A)

C), D), A), E), B)

No es correcto.

Así es, ese el orden correcto. Sólo los dos últimos pasos podrían ser intercambiables, aunque es más aconsejable el orden propuesto:

establecer los nombres de las variables y constantes del problema
escribir el problema de valor inicial (ecuación + condición inicial) que verifica la cantidad de sal disuelta
encontrar la solución general de la ecuación
imponer la condición particular
si en la ecuación hay un parámetro (por ejemplo en este caso tendremos la constante de proporcionalidad), determinarlo con el dato que proporciona el enunciado

Paso 1

Establecemos la siguiente notación

$t$: tiempo en horas
$x(t)$: cantidad de sal ya disuelta, en función del tiempo

Paso 2

Que 'la velocidad de disolución es proporcional a la cantidad de sal no disuelta y a la diferencia entre la concentración en el instante dado y la concentración de saturación' se escribe con la siguiente e.d.o.:

$$\frac{dx}{dt}=k(5-x)(x-\frac{1}{3})$$

$$\frac{dx}{dt}=kx(\frac{x}{60}-\frac{1}{3})$$

Ninguna de las opciones presentadas es correcta.

$$\frac{dx}{dt}=kx(\frac{5-x}{60}-\frac{1}{3})$$

$$\frac{dx}{dt}=k(5-x)(\frac{x}{60}-\frac{1}{3})$$

No es correcto, esa expresión no es dimensionalmente correcta.

Esta expresión es dimensionalmente correcta, pero no recoge la condición.

Sí hay una correcta.

Esta expresión es dimensionalmente correcta, pero no recoge la condición.

En efecto, ésta es la correcta, pues la cantidad no disuelta es la diferencia entre la cantidad inicial (5 Kg.) y la cantidad ya disuelta ($x$ Kg), mientras que la concentración en el instante dado es el cociente entre la cantidad disuelta y el volumen:

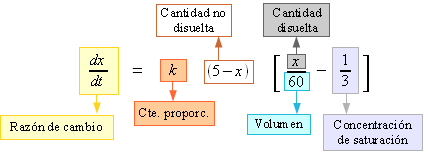
Gráfica

Escribe ahora el problema de valor inicial y pulsa en 'Continuar'.

Puesto que inicialmente el agua está limpia, el problema de valor inicial es $$\frac{dx}{dt}=k(5-x)(\frac{x}{60}-\frac{1}{3}) \hspace{1cm},\hspace{1cm} x(0)=0$$

Paso 3

La ecuación que debemos resolver es

Lineal

De variables separables y también lineal

De variables separables

Esta no es la propuesta correcta.

En efecto, se trata de una ecuación separable, que podemos escribir como $$\frac{dx}{(x-5)(x-20)}=-\frac{k}{60}\hspace{1cm},\hspace{1cm}x=5\hspace{1cm},\hspace{1cm}x=20$$ Las soluciones singulares no nos interesan en este caso, pues no cumplen la condición inicial. Encuentra la solución general de la ecuación y pulsa en 'Continuar'

La primitiva del miembro de la izquierda es de tipo racional, con dos raíces simples: $$\frac{1}{(x-5)(x-20)}=\frac{1}{15}\left(-\frac{1}{x-5}+\frac{1}{x-20}\right)$$ Luego la solución general debe cumplir $$\frac{1}{15}\log\left|\frac{x-20}{x-5}\right|=-\frac{k}{60}t+C_1$$ o bien $$\frac{x-20}{x-5}=Ce^{-\frac{k}{4}t}$$

Paso 4

De esa familia de soluciones nos interesa aquella que cumpla $x(0)=0$: $$x(0)=0 \hspace{1cm}\Rightarrow \hspace{1cm} \frac{-20}{-5}=4=Ce^0=C$$ es decir $$\frac{x-20}{x-5}=4e^{-\frac{k}{4}t}$$

Paso 5

Sólo falta aplicar la otra condición que da el enunciado, que nos conducirá al valor de la constante de proporcionalidad para este caso. Determina la solución y pulsa en 'Ver' cuando lo tengas.

Ver

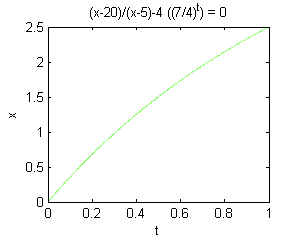
$$x(1)=\frac{5}{2} \hspace{1cm}\Rightarrow \hspace{1cm} \frac{5-40}{-5}=4e^{-\frac{k}{4}} \hspace{1cm}\Rightarrow \hspace{1cm} e^{-\frac{k}{4}}=\frac{7}{4}$$ Así que finalmente la cantidad de sal disuelta en función del tiempo es $$\frac{x-20}{x-5}=4\left(\frac{7}{4}\right)^t$$ Escribe ahora el código con el que representas en el ordenador la gráfica de $x(t)$ frente a $t$ entre $t=0$ y $t=1$. Pulsa en 'Continuar' cuando lo tengas.

% x(t) es la cantidad de sal disuelta actuando con 60 l de agua
f=@(t,x) (x-20)./(x-5)-4*((7/4).^t);
ezplot(f,[0 1 0 2.5])

Gráfica

Resolución del segundo apartado

Igual que en el apartado anterior, hemos de conocer la expresión que relaciona la cantidad de sal disuelta y el tiempo, para así saber cuál es la cantidad que se ha disuelto en una hora. Para ello hemos de establecer de nuevo cuál es la razón de cambio de esa cantidad de sal disuelta respecto del tiempo. Escribe esa ecuación y pulsa en 'Ver'

Ver

Puesto que el volumen es 120 litros, la ecuación resulta $$\frac{dx}{dt}=k(5-x)(\frac{x}{120}-\frac{1}{3})$$ siendo $k$ tal que $$e^{-\frac{k}{4}}=\frac{7}{4}$$ Esto es así porque el valor de la constante de proporcionalidad, $k$, no depende de cuál sea el volumen de agua con el que se esté actuando, así que debemos tomar el obtenido en el apartado anterior. Encuentra la solución general y pulsa en 'Continuar'.

Siguiendo una resolución paralela a la realizada en el primer apartado se obtiene como solución general $$\frac{x-40}{x-5}=Ce^{-\frac{7k}{24}t}$$ Aplicando la condición inicial, $x(0)=0$, determinamos el valor de $C$ que nos lleva a la solución particular siguiente $$\frac{x-40}{x-5}=8e^{-\frac{7k}{24}t}$$ Teniendo en cuenta que $e^{-\frac{k}{4}}=\frac{7}{4}$, $$e^{-\frac{k}{4}}=\frac{7}{4} \hspace{1cm}\Rightarrow \hspace{1cm} e^{-\frac{7k}{24}}=(e^{-\frac{k}{4}})^\frac{7}{6}=(\frac{7}{4})^\frac{7}{6}$$ la expresión de la solución es $$\frac{x-40}{x-5}=8(\frac{7}{4})^{\frac{7}{6}t}$$

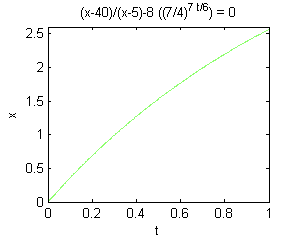
Gráfica

Utiliza esta expresión para hallar la cantidad disuelta en una hora. Pulsa en 'Ver' cuando lo tengas.

Ver

Para $t=1$, $$\frac{x(1)-40}{x(1)-5}=8(\frac{7}{4})^\frac{7}{6} \hspace{1cm}\Rightarrow \hspace{1cm} x(1)=40\frac{1-a}{1-8a}$$ donde $$a=(\frac{7}{4})^\frac{7}{6}$$ Utilizando calculadora u ordenador calculamos una expresión decimal de $x(1)$, $$x(1)\approx 2.5641$$ Así pues la diferencia entre actuar con 60 litros de agua o con el doble es sólo de 64 gramos más de sal disueltos (en una hora).

Resolución del tercer apartado

Para trazar una gráfica de la cantidad de sal disuelta en 1 hora respecto del volumen de agua utilizado, debemos determinar la función que relaciona esas dos magnitudes. El proceso que se siguió en el apartado anterior con un volumen de 120 litros debemos seguirlo ahora para un volumen cualquier, sea $V$. La ecuación diferencial es ... escríbela y pulsa en 'Ver'.

Ver

$$\frac{dx}{dt}=k(5-x)(\frac{x}{V}-\frac{1}{3}) \hspace{1cm} \mbox{siendo} \hspace{1cm} e^{-\frac{k}{4}}=\frac{7}{4}$$ o bien $$\frac{dx}{(x-5)(x-V/3)}=\frac{-k}{V}\, dt$$ Busca los coeficientes $A$ y $B$ de la descomposición $$\frac{1}{(x-5)(x-V/3)}=\frac{A}{x-5}+\frac{B}{x-V/3}$$ y pulsa en 'Continuar'.

Tenemos que $$\frac{1}{(x-5)(x-V/3)}=\frac{1}{V/3-5}\left(\frac{-1}{x-5}+\frac{1}{x-V/3}\right)$$ Por tanto, la solución general de la ecuación anterior es $$\frac{x-V/3}{x-5}=Ce^{-kMt}$$ donde se ha llamado $$M=\frac{V/3-5}{V}=\frac{1}{3}-\frac{5}{V}$$ Busca ahora la solución particular correspondiente a $x(0)=0$.

Ver

$$x(0)=0 \hspace{1cm} \Rightarrow \hspace{1cm} \frac{V}{15}=C \hspace{1cm} \Rightarrow \hspace{1cm} \frac{x-V/3}{x-5}=\frac{V}{15}e^{-kMt}$$ Puesto que $e^{-\frac{k}{4}}=\frac{7}{4}$, $$e^{-k}=(\frac{7}{4})^4$$ y sustituyendo en la expresión de la solución, $$\frac{x-V/3}{x-5}=\frac{V}{15}(\frac{7}{4})^{4Mt}$$ Ahora podemos determinar la cantidad de sal disuelta en 1 hora para cualquier volumen $V$. Halla la expresión de esa cantidad en función de $V$ y pulsa en 'Continuar'.

$x(1)$ cumple $$\frac{x(1)-V/3}{x(1)-5}=\frac{V}{15}(\frac{7}{4})^{4Mt}$$ despejando, $$x(1)=\frac{V/3-5b}{1-b} \hspace{1cm} \mbox{con} \hspace{1cm} b=\frac{V}{15}(\frac{7}{4})^{4M}$$ Podemos representar esta cantidad frente al volumen $V$ con el siguiente código

% Q(V) es la cantidad de sal disuelta actuando con V litros de agua
M=@(V) 1/3-5./V;
b=@(V) V.*(7/4).^(4*M(V))/15;
Q=@(V)(V/3-5*b(V))./(1-b(V));
vV=60:10:300;
vQ=Q(vV);
plot(vV,vQ)
xlabel('V');ylabel('Q')

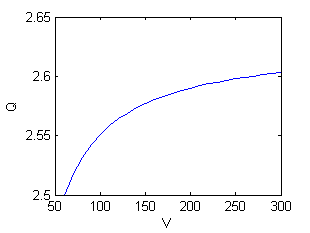
Gráfica

Observando los valores de la cantidad de sal disuelta concluimos que se gana muy poco aumentando la cantidad de agua, como ya habíamos visto en el segundo apartado al duplicarla. De hecho, el límite de la función $Q(V)$ es 2.6291. Podemos calcular este límite con el código

%%%%%%% límite de la cantidad de sal disuelta en una hora
syms v
m=1/3-5/v;
b=v*((7/4)^(4*m))/15;
q=(v/3-5*b)/(1-b);
double(limit(q,v,Inf))

Para disolver más cantidad de sal, debería dejarse actuar el agua durante más tiempo. Por ejemplo, con 60 litros de agua, la cantidad de sal disuelta en 2 horas es $$x(2)=\frac{20-5*b}{1-b}\hspace{1cm} \mbox{con} \hspace{1cm} b=4(\frac{7}{4})^{8M} \hspace{1cm} \mbox{y} \hspace{1cm} M=\frac{15}{60}=\frac{1}{4}$$ es decir, $$x(2)=\frac{20-5*49/4}{1-49/4}\approx 3.6667$$

Índice de tema