Enunciado
Según la ley de Newton, la velocidad de enfriamiento de un cuerpo en el aire es proporcional a la diferencia entre la temperatura del cuerpo y la temperatura del aire. Si la temperatura del aire es de 10 grados y el cuerpo se enfría en 3 minutos desde 40 a 25 grados,
- ¿cuánto tiempo más ha de pasar para que su temperatura descienda hasta los 15 grados?
- ¿cuándo estará a temperatura ambiente? (Para contestar a esta pregunta considera que la variación admisible de la temperatura ambiente es de 1 centésima de grado)
- Representa la función temperatura del cuerpo respecto del tiempo.
Resolución del primer apartado
Para contestar a la pregunta de este primer apartado hemos de conocer la expresión de la función temperatura respecto del tiempo. Para hallar esta expresión debemos:
- establecer los nombres de las variables y constantes del problema
- escribir el problema de valor inicial (ecuación + condición inicial) que verifica la temperatura del cuerpo
- encontrar la solución general de la ecuación
- imponer la condición particular
- si en la ecuación hay un parámetro (por ejemplo en este caso tendremos la constante de proporcionalidad), determinarlo con el dato que proporciona el enunciado
Paso 1
Establecemos la siguiente notación- $t$: tiempo en minutos
- $T(t)$: temperatura en grados centígrados del cuerpo en función del tiempo
- $T_m$: temperatura ambiente en grados centígrados (constante)
Paso 2
Escribe el hecho de que la temperatura cambie proporcionalmente a su diferencia con la temperatura ambiente en forma de ecuación diferencial. Piensa también cuál es la condición inicial. Pulsa en 'Ver' cuando lo tengas.
Ver
Si tomamos el criterio de que $k$ sea positiva, escribiremos
$$\frac{dT}{dt}=-k(T-T_m)$$
ecuación que acompañamos con la condición inicial $T(0)=40$.
Paso 3
La solución general de la ecuación diferencial anterior es
$T-T_m=e^{-kt}+C$
$T-T_m=-ke^{t}+C$
Ninguna de las dos opciones es correcta.
No es correcto, revisa el cálculo.
No es correcto, revisa el cálculo.
En efecto, ninguna de las dos opciones es correcta:
$$\frac{dT}{dt}=-k(T-T_m) \hspace{1cm}\Rightarrow \hspace{1cm} \frac{dT}{T-T_m}=-k\, dt
\hspace{1cm}\Rightarrow \hspace{1cm} \log|T-T_m|=-Kt+C_1
\hspace{1cm}\Rightarrow \hspace{1cm} $$
$$\hspace{1cm}\Rightarrow \hspace{1cm} |T-T_m|=e^{C_1}e^{-Kt} \hspace{1cm}\Rightarrow \hspace{1cm} T-T_m=Ce^{-Kt}\hspace{.4cm},\hspace{.5cm} C\in{\bf R}$$
Puesto que en este caso $T_m=10$, la solución general es $$T=10+Ce^{-Kt}$$
Paso 4
Aplica la condición inicial para determinar el valor de la constante $C$. Pulsa en 'Continuar' cuando lo tengas.
$$T(0)=40=10+C \hspace{1cm}\Rightarrow \hspace{1cm} C=30$$
y la solución particular es $$T=10+30e^{-Kt}$$
Todavía no está completamente determinada pues no conocemos el valor de la constante de proporcionalidad. Para saberlo debemos aplicar el dato del enunciado que todavía no ha sido utilizado. Inténtalo y pulsa en 'Ver'.
Ver
La temperatura del cuerpo es de 25 grados para $t=3$ luego
$$T(3)=10+30e^{-3k}=25\hspace{1cm}\Rightarrow \hspace{1cm} e^{-3k}=\frac{1}{2}
\hspace{1cm}\Rightarrow \hspace{1cm} e^{-k}=2^{-1/3}$$
Observa que no es preciso calcular $k$, sino que es mejor introducir directamente el factor $e^{-k}$ en la expresión de la solución:
$$T=10+30e^{-Kt}=10+30\cdot 2^{-t/3}$$
Paso 5
Ahora ya podemos calcular el tiempo necesario para que la temperatura del cuerpo sea de 15 grados. Si $t_f$ es ese valor del tiempo, $$10+30\cdot 2^{-t_f/3}=15 \hspace{1cm}\Rightarrow \hspace{1cm} 2^{t_f/3}=6 \hspace{1cm}\Rightarrow \hspace{1cm} t_f=3\frac{\log 6}{\log 2}=3\left(1+\frac{\log 3}{\log 2}\right)$$ por lo que el tiempo que debe pasar desde los tres minutos es $$t=3\frac{\log 3}{\log 2}\approx 4.75$$Resolución del segundo apartado
Del apartado anterior sabemos que la función temperatura del cuerpo respecto del tiempo es $$T(t)=10+30\cdot 2^{-t/3}$$ La temperatura ambiente es de 10 grados. ¿Existe algún valor de $t$ para el cual $T(t)=10$?
Sí.
No.
No es cierto, pues el factor $2^{-t/3}$ no se anula para ningún valor de $t$. La función temperatura decrece asintóticamente hacia 10.
En efecto, pues el factor $2^{-t/3}$ no se anula para ningún valor de $t$. La función temperatura decrece asintóticamente hacia 10. El cuerpo se va enfriando tendiendo su temperatura a la ambiente.
Pero en la realidad, se considera que dos temperaturas son iguales si su diferencia es menor que un cierto umbral. En el enunciado se plantea la igualdad cuando la diferencia es de una centésima o menor. Busca con este criterio el valor del tiempo en que consideraremos que el cuerpo está a temperatura ambiente. Pulsa en 'Continuar' cuando lo tengas.
Puesto que $T(t)$ tiende a 10 superiormente, pondremos
$$T(t)=10+30\cdot 2^{-t/3}=10+10^{-2}$$
de donde $$2^{t/3}=3000$$
y de aquí $$t=3\frac{\log 3000}{\log 2}\approx 34.65$$
Resolución del tercer apartado
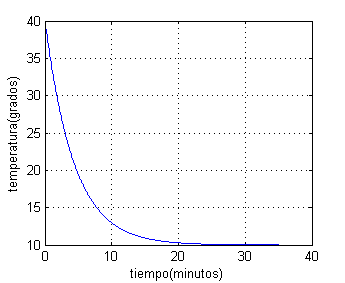
Escribe el código con el que trazas la gráfica de la función temperatura frente al tiempo tomando desde $t=0$ a $t=35$. Pulsa en 'Ver' cuando lo tengas.
Ver
%%% gráfica de la función temperatura T=10+30/2^(t/3)
figure(1)
t=0:.1:35;
plot(t,10+30./2.^(t/3))
grid on
xlabel('tiempo(minutos)');ylabel('temperatura(grados)')
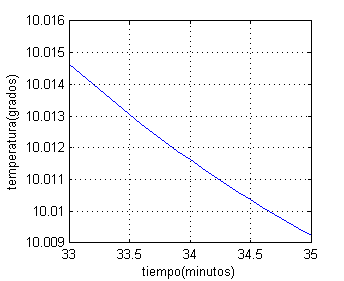
Traza ahora, en otra ventana de figuras, el detalle de la gráfica anterior en los últimos tres minutos, es decir, tomando $t$ desde 33 a 35. Pulsa en 'Ver' cuando lo tengas.
Ver
%%% detalle de la misma función en los últimos 3 minutos
figure(2)
t=33:.1:35;
10+30./6.^(t/3)
plot(t,10+30./2.^(t/3))
grid on
xlabel('tiempo(minutos)');ylabel('temperatura(grados)')