Enunciado
Un depósito cilíndrico de eje vertical y sección transversal $S$, tiene un orificio en su fondo de área $s$, cerrado por una tapa. El recipiente contiene agua hasta una altura $h$. En el instante $t=0$, la tapa comienza a abrirse de manera que el área abierta es proporcional al tiempo transcurrido desde que empezó a abrise. Si $T$ es el tiempo que tarda en abrise completamente el orificio, expresa en función de $T$ la altura de agua en ese momento.
En primer lugar establecemos la notación que utilizaremos en toda la resolución:
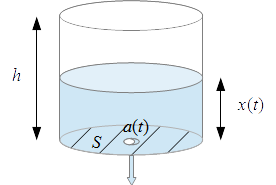
- $S$: área de la base del depósito;
- $s$: área del orificio de salida;
- $T$: tiempo que tarda en abrise el orificio de salida.
- $t$: tiempo (variable independiente del modelo);
- $x(t)$: altura de agua en el depósito en el momento $t$;
- $V(t)$: volumen de agua en el depósito en el momento $t$;
- $a(t)$: area de salida abierta en el momento $t$;
- la tasa de entrada de agua al depósito es nula, pues en el enunciado no se indica entrada de agua;
- la tasa de salida de agua del depósito se establece teniendo en cuenta que
- el volumen que sale por unidad de tiempo es el producto de la velocidad de salida por el área de salida abierta y
- la velocidad de salida es la misma que si el agua cayera desde el nivel de agua hasta el orificio (Ley de Torricelli): $\sqrt{2g x(t)}$, siendo $g$ la aceleración de la gravedad.
Ver
$$\frac{dV}{dt}=-a(t)\sqrt{2g x(t)}$$
Ahora debemos poner todo en términos de $x(t)$ y de $t$, para lo cual es preciso escribir $V(t)$ en función de $x(t)$. Por una parte, puesto que el depósito es cilíndrico sabemos que $V(t)=S x(t)$
El enunciado establece que $a(t)$ es proporcional a $t$, luego existe $k$ tal que $a(t)=kt$; pero puesto que para $t=T$ el orificio ya está completamente abierto, tendremos $a(T)=s$, es decir, $kT=s$, de donde $k=s/T$ y por tanto $$a(t)=\frac{s}{T}t$$ Así pues el problema de valor inicial que debe verificar la función $x(t)$ es, ... escríbelo y pulsa en 'Ver'.
Ver
$$\frac{dx}{dt}(t)=-\frac{s}{ST}\sqrt{2g}t\sqrt{x(t)}\ \ ,\ \ x(0)=h$$
Resuélvelo y pulsa en 'Continuar'.
La solución del problema es
$$\sqrt{x(t)}=\frac{-s}{4ST}\sqrt{2g}\,t^2+\sqrt{h}$$ Cuando $t=T$, se cumplirá que
$$\sqrt{x_T}=\frac{-s}{4S}\sqrt{2g}\,T+\sqrt{h}$$
De aquí ya podemos deducir cuánto vale $x_T$.
Hacen falta más datos.
$x_T$ no puede deducirse sin más, hay distintos casos que analizar debido a que $\sqrt{x_T}$ no puede ser negativo.
En efecto, hay dos casos que analizar debido a que $\sqrt{x_T}$ no puede ser negativo:
- Si $\sqrt{h}-\frac{s}{4S}\sqrt{2g}\,T$ es positivo, entonces $H=\left(\sqrt{h}-\frac{s}{4S}\sqrt{2g}T\right)^2$
- Si $\sqrt{h}-\frac{s}{4S}\sqrt{2g}\,T$ es negativo o nulo, entonces $H=0$, es decir, el depósito se vacía antes de que el orifico termina de abrirse.
Podríamos definir un valor $T_c$ crítico tal que
$\sqrt{h}-\frac{s}{4S}\sqrt{2g}\,T_c=0$, es decir $$T_c=\frac{4S\sqrt{h}}{s\sqrt{2g}}$$
de manera que
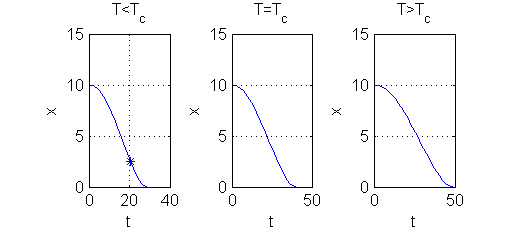
- Si $T< T_c$, entonces hay agua hasta después de $T$:
- la altura de agua cuando el orificio se abre del todo es $H=\left(\sqrt{h}-\frac{s}{4S}\sqrt{2g}T\right)^2$
- el agua se terminaría para $t_f=\sqrt{T_cT}>T$
- Si $T=T_c$, entonces hay agua hasta justo el momento $T$
- Si $T>T_c$, entonces el agua se termina antes de $T$, en el momento $t_f=\sqrt{T_cT}<T$
- Si por ejemplo tomamos $T=T_c-20$, entonces $H=2.45$ es la altura de agua cuando se termina de abrir el orificio ($t=20.39$) y el depósito se vacía para $t_f=28.7$;
- Si $T=T_c=40.39$, entonces hay agua hasta justo hasta que el orificio termina de abrirse;
- Si $T=T_c+20$, entonces el agua se termina en el momento $t_f=49.38$