Enunciado
La velocidad de una bola perforada en movimiento vertical sujeto a amortiguamiento viscoso (es decir, el rozamiento depende de la velocidad) está dada por la e.d.o. de primer orden
$$\frac{dv}{dt}=-g-\frac{k}{m}v$$
donde $g$, $k$ y $m$ son constantes positivas: $g$ es la aceleración de la gravedad, $k$ es la constante de viscosidad y $m$ es la masa.
- Modifica la magnitud de las variables de estado y tiempo de modo que la e.d.o. carezca de esas constantes.
- Resuelve la nueva e.d.o.
- Representa en el ordenador al menos nueve de esas soluciones.
- Si el movimiento empieza a altura 0, representa las alturas que toma la bola para las nueve funciones velocidad anteriores.
- ¿Cual es la velocidad límite de la e.d.o original?
Resolución del primer apartado
Para eliminar las constantes de la ecuación hemos de
- plantear un cambio de variables del tipo $$t=c_1x \hspace{1cm},\hspace{1cm} v=c_2y$$
- obtener $\frac{dv}{dt}$ en función de $\frac{dy}{dx}$
- sustituirlo en la ecuación
- forzar a que la nueva ecuación no tenga parámetros para obtener la expresión de $c_1$ y $c_2$.
Puesto que $$t=c_1x \hspace{1cm},\hspace{1cm} v=c_2y$$
aplicando la regla de la derivación compuesta o regla de la cadena, sabemos que
$v$ es función de $y$ que a su vez es función de $t$, luego
$$\frac{dv}{dt}=\frac{dv}{dy}\frac{dy}{dt}$$
$v$ es función de $y$ y también es función de $t$ y ambas son función de $x$, luego
$$\frac{dv}{dt}=\frac{dv}{dy}\frac{dy}{dx}+\frac{dv}{dt}\frac{dt}{dx}$$
Ninguna de las propuestas es correcta.
$v$ es función de $y$, que es función de $x$ que a su vez depende de $t$, luego
$$\frac{dv}{dt}=\frac{dv}{dy}\frac{dy}{dx}\frac{dx}{dt}$$
Es correcto, pero incompleto. Recuerda que debemos escribir $\frac{dv}{dt}$ en función de $\frac{dy}{dx}$.
Eso no tiene ningún sentido.
Sí hay una opción correcta.
En efecto, puesto que debemos expresar $\frac{dv}{dt}$ en función de $\frac{dy}{dx}$, la cadena de dependencia correcta es la de esta propuesta; ahora
$$\frac{dv}{dy}=c_2 \hspace{.5cm}, \hspace{.5cm} \frac{dx}{dt}=\frac{1}{c_1}
\hspace{1cm} \Rightarrow \hspace{1cm} \frac{dv}{dt}=\frac{c_2}{c_1}\frac{dy}{dx}$$
y la e.d.o. inicial se convierte en
$$\frac{dy}{dx}=-\frac{c_1}{c_2}g-\frac{k}{m}c_1y$$
Paso 2
Para que esta ecuación no tenga parámetros, debemos hacer
$-\frac{c_1}{c_2}g=1$ y $-\frac{k}{m}c_1=1$
Las dos opciones propuestas son correctas.
$\frac{c_1}{c_2}g=1$ y $\frac{k}{m}c_1=1$
Así la e.d.o. carecerá en efecto de constantes, pero es preferible que la nueva variable $x$ represente al tiempo y la nueva velocidad, $y$ tenga el mismo signo que la $v$; esto no se cumple si $c_1$ y $c_2$ son negativas.
Hay una mejor que la otra.
En efecto ésta es la mejor opción, pues siendo $c_1$ y $c_2$ positivas la variable $x$ es el tiempo y la $y$ es la velocidad del mismo signo que $v$. Obtén las expresiones de $c_1$ y $c_2$ en función de los parámetros $m$, $k$ y $g$; pulsa en 'Continuar' cuando lo tengas.
Tenemos $$c_1=\frac{m}{k} \hspace{.5cm}, \hspace{.5cm} c_2=\frac{m}{k}g$$
luego el cambio de variables buscado es
$$t=\frac{m}{k}x \hspace{.5cm}, \hspace{.5cm} v=\frac{m}{k}g y$$
y la nueva ecuación es $$\frac{dy}{dx}=-1-y$$
Resolución del segundo apartado
Hemos de resolver la ecuación anterior. Se trata de una ecuación de variables separables, equivalente a $$\frac{dy}{y+1}=-dx \hspace{.5cm} \mbox{o} \hspace{.5cm} y=-1 $$ Encuentra la solución general y pulsa en 'Ver' cuando la tengas.
Ver
La solución general es $$y(x)=Ce^{-x}-1$$
Tomando $C$ cualquier número real, esta familia incluye a la solución singular $y=-1$.
Resolución del tercer apartado
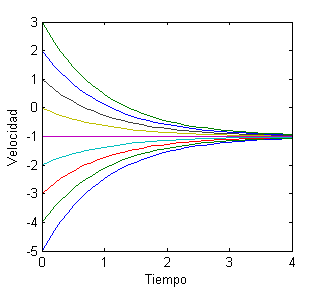
En este apartado hay que representar nueve curvas de esa familia de soluciones. Podemos representar las correspondientes a $C$ desde $-4$ a $4$ en el intervalo $[0,4]$ con el siguiente código:
x=0:.1:4;
c=-4:4;
[X,C]=meshgrid(x,c);
Y=C.*exp(-X)-1;
plot(x,Y)
xlabel('Tiempo');ylabel('Velocidad')
Resolución del cuarto apartado
Debemos representar ahora nueve funciones del espacio recorrido por la bola. Puesto que conocemos las funciones velocidad, para encontrar las funciones espacio hemos de ... piénsalo y pulsa en 'Ver'
Ver
Obtendremos la familia de funciones espacio integrando la familia de velocidades:
$$s(x)=\int y(x)\, dx=\int (Ce^{-x}-1)\, dx=-Ce^{-x}-x+K$$
Puesto que se parte del reposo,
$$s(0)=0 \hspace{1cm}\Rightarrow \hspace{1cm} -C+K=0 \hspace{1cm}\Rightarrow \hspace{1cm}
s(x)=C(1-e^{-x})-x$$
Representamos ahora las correspondientes a $C$ desde $-4$ a $4$ en el intervalo $[0,4]$. Escribe un código con ese efecto y pulsa en 'Ver'.
Ver
Podemos escribir
x=0:.1:4;
c=-4:4;
[X,C]=meshgrid(x,c);
S=C.*(1-exp(-X))-X;
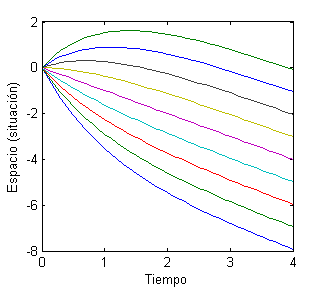
plot(x,S)
xlabel('Tiempo');ylabel('Espacio (situación)')
A la figura resultante le adjuntamos a la derecha la figura con las velocidades para poder observar mejor la correspondencia entre las curva espacio y velocidad:
|

|
Del comportamiento de estas curvas deducimos que si la velocidad (variable $y$) inicial es negativa, siempre permanece negativa, tendiendo a $y=-1$; si la bola comienza cayendo seguirá siempre cayendo con velocidad decreciente en valor absoluto. Si la bola comienza su movimiento hacia arriba, en un momento dado se parará y empezará a descender.