Método de Euler

El método de las tangentes o método de Euler nos da una primera aproximación de los valores que toma la solución del problema de valor inicial $$\left\{\begin{array}{ll} y'=f(x,y)\\ y(x_0)=y_0\end{array}\right.$$ sobre un conjunto de puntos dados.

Lo primero que debemos hacer es asegurnos de que este problema tiene solución única $y=y(x)$ en un intervalo centrado en $x_0$. Se fija $h>0$ y se consideran los puntos $$x_n=x_0+nh\ ,\ \ n=0,\, 1,\, 2,\, \ldots$$ La recta tangente a la solución $y=y(x)$ en el punto $(x_0,y_0)$ tiene pendiente igual a $f(x_0,y_0)$, luego su ecuación es $$y=y_0+(x-x_0)f(x_0,y_0)$$ en particular, para el punto $x_1=x_0+h$ el valor de la recta tangente resulta $$y_1=y_0+hf(x_0,y_0)$$ y proporciona la aproximación lineal del valor $y(x_1)$ desconocido. Nos situamos ahora en el punto $(x_1,y_1)$, consideramos la recta con pendiente dada por $f(x_1,y_1)$ y la evaluamos en $x_2=x_1+h$, para obtener $$y_2=y_1+hf(x_1,y_1)$$ como aproximación del valor $y(x_2)$ desconocido. De esta manera se ha calculado una aproximación para el valor de la solución en $x_2$ utilizando la aproximación calculada para $x_1$. Así obtenemos las siguientes fórmulas recursivas:

$$\left\{\begin{array}{l}y_{n+1}=y_{n}+hf(x_n,y_n) \\ x_{n+1}=x_n+h\end{array}\right.\ ,\ \ n=0,\, 1,\, 2,\, \ldots$$ Estas fórmulas determinan los vértices de una línea poligonal que aproxima la solución del problema de valor inicial sobre los puntos $x_n$. Si se desea aproximar la solución del problema en $x=c$, deberemos hallar el paso $h$ tal que $x_0+nh=c$ para algún entero $n$.

Método de Euler mejorado

Los errores en la aproximación conseguida con las fórmulas anteriores disminuyen tomando un valor menor para $h$, pero eso supone más operaciones y por tanto mayor riesgo de errores de redondeo.

Un método de búsqueda de una solución aproximada $y(x;h)$ para la solución exacta $\phi(x)$ converge si $\lim_{h\rightarrow 0}y(x;h)=\phi(x)$ y es de orden $p$ (o su velocidad de convergencia es $p$) si $\phi(x)-y(x;h)=O(h^p)$.

La velocidad de convergencia del método de Euler presentado antes es $p=1$; esto significa que por ejemplo, para conseguir un error menor que $10^{-2}$ se necesitarán normalmente más de $100$ pasos. Una mejora sencilla es el llamado Método de Euler mejorado. La mejora radica en que para estimar $y(x_1)$ utilizaremos no sólo la pendiente en $(x_0,y_0)$, sino la media entre las pendientes en $(x_0,y_0)$ y en $(x_1,y_0+hf(x_0,y_0))$; nótese que $y_0+hf(x_0,y_0)$ es el valor estimado para la solución $y(x)$ en $x=x_1=x_0+h$ por el método de Euler.

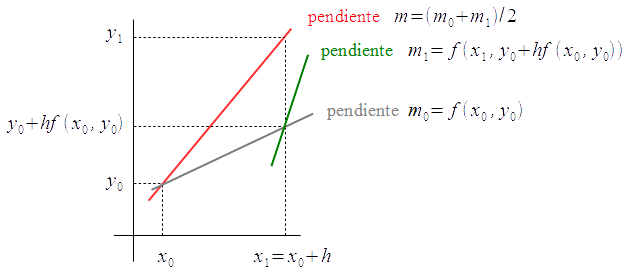
La recta que pasa por $(x_0,y_0)$ con pendiente $$m=\frac{1}{2}[f(x_0,y_0)+f(x_1,y_0+hf(x_0,y_0))]$$ es $$y=y_0+\frac{1}{2}[f(x_0,y_0)+f(x_1,y_0+hf(x_0,y_0))](x-x_0)$$ La ordenada de esta recta para $x=x_1=x_0+h$, $$y_1=y_0+\frac{h}{2}[f(x_0,y_0)+f(x_1,y_0+hf(x_0,y_0))]\ \ \ ,\ \ \ \mbox{con} \ \ x_1=x_0+h$$ es una aproximación de la solución $y(x)$ en $x=x_1$. Este es el primer paso por el cual se ha obtenido la aproximación de $y(x_1)$; este proceso se va repitiendo sucesivamente, siguiendo la fórmula recursiva

$$y_{n+1}=y_{n}+\frac{h}{2}\left[f(x_n,y_n)+f(x_n+h,y_n+hf(x_n,y_n))\right]\ ,\ \ n=0,\, 1,\, 2,\, \ldots$$

Como se verá en los ejercicios, con esta fórmula se gana mucha precisión respecto del primer método. De hecho, se puede demostrar que el método de Euler mejorado converge con velocidad $p=2$.