La base de los métodos de Runge-Kutta es mejorar la aproximación de la solución del problema $$\left\{\begin{array}{ll} y'=f(x,y)\\ y(x_0)=y_0\end{array}\right.$$ sin tener que recurrir a las derivadas de orden superior a uno. En ellos se recurre a una media ponderada de los valores de $f$ en distintos puntos. La elección de esos puntos y de los coeficientes de la combinación genera una gran familia de métodos. Describiremos aquí el método de Runge-Kutta clásico de orden 4. Su formulación es

$$x_{n+1}=x_n+h\ \ \ ,\ \ \ y_{n+1}=y_n+\frac{h}{6} (K_1+2K_2+2K_3+K_4)$$ donde \begin{eqnarray*} K_1 &=& f(x_n,y_n) \\ K_2 &=& f(x_n+\frac{h}{2},y_n+\frac{h}{2}K_1) \\ K_3 &=& f(x_n+\frac{h}{2},y_n+\frac{h}{2}K_2) \\ K_4 &=& f(x_n+h,y_n+hK_3) \end{eqnarray*}

El origen de estas fórmulas es el siguiente:

1. Se calcula la pendiente en el punto $(x_n,y_n)$ $$K_1 = f(x_n,y_n)$$

   

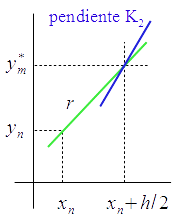
2. Se toma la recta tangente en $(x_n,y_n)$ $$r: \ y=y_n+K_1(x-x_n)$$ y se evalúa en $x=x_n+\frac{h}{2}$; sea $$y_m^*=y_n+\frac{h}{2}K_1$$ $y_m^*$ es una estimación del valor de la solución en $x=x_n+\frac{h}{2}$

   

3. Se evalúa $f$ en $(x_n+\frac{h}{2},y_m^*)$: $$K_2 = f(x_n+\frac{h}{2},y_n+\frac{h}{2}K_1)$$

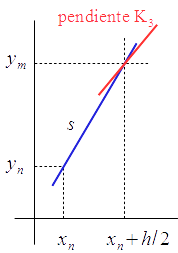
4. Se revisa la estimación $y_m^*$ utilizando $K_2$: $$y_m=y_n+\frac{h}{2}K_2$$ es la ordenada de la recta que pasa por $(x_n,y_n)$ con pendiente $K_2$, $$s: \ y=y_n+K_2(x-x_n)$$ correspondiente a $x=x_n+\frac{h}{2}$

5. Se evalúa $f$ en $(x_n+\frac{h}{2},y_m)$: $$K_3 = f(x_n+\frac{h}{2},y_n+\frac{h}{2}K_2)$$

   

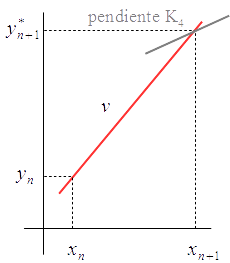
6. Utilizando la recta que pasa por $(x_n,y_n)$ con pendiente $K_3$, $$v: \ y=y_n+K_3(x-x_n)$$ se hace una primera estimación del valor de la solución en $x_{n+1}$, $$y_{n+1}^*=y_n+hK_3$$

7. Se evalúa $f$ en $(x_{n+1},y_{n+1}^*)$: $$K_4 = f(x_n+h,y_n+hK_3)$$