Disolución en un tanque

Se considera un tanque o depósito con un volumen inicial dado, $V_0$ litros (L) de una cierta disolución. Inicialmente la cantidad de soluto es $Q_0$. En el momento $t=0$ se comienza a verter disolución con una concentración dada por $C_e$ Kg/L a razón de $F^e$ L/min.\ y a dejar salir disolución a razón de $F^s$ L/min. El balance de masa de soluto en el depósito es $$\mbox{Masa acumulada}=\mbox{Masa entrante}-\mbox{Masa saliente}$$ Si llamamos $C(t)$ a la concentración de soluto en el tanque en el momento $t$ y $V(t)$ es el volumen, la masa en el momento $t$ será $Q(t)=V(t)C(t)$. Así pues, obtener un modelo para la concentración o hacerlo para la masa son problemas equivalentes. Para un incremento $\Delta t$ del tiempo, el balance de masas es $$\Delta Q=C_eF^e\Delta t -\frac{Q}{V}F^s\Delta t$$ Podemos escribir esta relación en términos de diferenciales, $$dQ=(C_eF^e-\frac{Q}{V}F^s)\, dt$$ o bien $$\frac{dQ}{dt}=C_eF^e-\frac{Q}{V}F^s$$ ambos miembros de esta ecuación tienen unidades de Masa entre Tiempo, en este caso Kg/min; cada uno de los factores del miembro derecho llega a esas unidades como resultado de multiplicar Kg/L por L/min (concentración por flujo). Esta es la ecuación que habríamos obtenido partiendo de la relación entre las tasas o razones de cambio de la masa: $$\mbox{Tasa acumulación}=\mbox{Tasa de entrada}-\mbox{Tasa de salida}$$

Demanda bioquímica de oxígeno

Los ríos y arroyos contienen microorganismos que utilizan materia orgánica, como por ejemplo aguas residuales, para crecer. Por acción bioquímica aerobia, el oxígeno es utilizado para descomponer la materia orgánica. La DBO (BOD en inglés) es la cantidad de oxígeno necesaria para descomponer la materia orgánica presente. Esta medida resulta esencial en el estudio de la calidad del agua, mayor DBO indica mayor contaminación por materia orgánica.

Supongamos que se ha producido un vertido de aguas residuales; en los primeros días aumentarán los microorganismos existentes en la corriente junto con la demanda de oxígeno; pasados unos días de este proceso de oxidación, comenzamos a analizar la cantidad demandada de oxígeno (sea $L(t)$) en función del tiempo (t). Se puede comprobar que, supuesta la temperatura constante, $$\frac{dL}{dt}=-kL$$ donde $k$ es la constante de desoxigenación. Esta constante define las características propias del agua residual y puede oscilar de $0.12$ a $0.70$ $\mbox{días}^{-1}$. Un valor típico es $k=0.23\, \mbox{días}^{-1}$, para aguas contaminadas y residuales a $20^o\mbox{C}$. La ecuación anterior se acompaña de la condición $L=L_0$ para $t=0$, siendo $L_0$ la DBO total.

Reacción química simple

En las reacciones químicas más simples, la razón de cambio en que una sustancia $A$ se transforma en otra es proporcional a la cantidad de $A$ existente. Si llamamos $x(t)$ a la cantidad inicial de $A$, esta característica se escribe $$\frac{dx}{dt}=-kx$$ donde la constante $k$ introduce en la ecuación lo rápido que se produce la reacción. Este valor $k$ es propio de la sustancia $A$ y las condiciones en que se esté desarrollando la reacción. Si su valor no es conocido, serán precisos dos datos de cantidad de $A$, en $t=0$ y en otro valor del tiempo:

• La cantidad inicial, $x(0)$, acompañará a la ecuación para formar un problema de valor inicial y se utilizará para encontrar la forma de su solución particular.

• El dato en otro valor de tiempo se impondrá a la solución anterior para determinar el valor de $k$ y con ello la función $x(t)$.

Esta formulación la encontraremos por ejemplo en reacciones radioactivas y en otros procesos como la datación con carbono o modelos simples de población, en los que la variación de la variable dependiente es proporcional a su valor.

Cambio de temperatura de un objeto

Experimentalmente se ha comprobado que la temperatura de un cuerpo cambia proporcionalmente a la diferencia entre su temperatura y la del medio en que se encuentra. Esta es una formulación básica de la ley de enfriamiento de Newton. Si para el momento en que se empieza a estudiar el proceso, $t=0$, la temperatura del cuerpo es $T(0)=T_0$, y la temperatura del medio es $T_m$, la propiedad anterior es $$\frac{dT}{dt}=-k(T-T_m)$$ La ecuación irá acompañada de la condición inicial $T(0)=T_0$ y deberemos contar con otro dato de la temperatura para determinar el valor de la constante $k$ al igual que ocurría en la aplicación anterior.

Modelos simple y logístico de población

En el modelo simple para la población (número de individuos en un área determinada) se supone que no hay interacción con la propia ni con otras especies y que no hay cambios por migración. La ecuación obtenida bajo esos supuestos es la de la aplicación 'Reacción química simple', únicamente cambia el significado de las variables. Sin embargo, si suponemos competencia entre los individuos obtenemos una ecuación logística $$\frac{dp(t)}{dt}=ap-bp^2$$ donde $a$ y $b$ son parámetros que habrá que calcular utilizando los datos propios de cada caso.

Flujo del calor en una dimensión en estado estacionario

El flujo de calor en una dimensión se gobierna por la ecuación $$H=kA\frac{dT}{dr}$$ donde $H$ es la cantidad de calor fluyendo a través de un material (en cal$/$seg), $k$ es el coeficiente de conductividad térmica (en cal$/$($^o$C cm seg), $A$ es el área perpendicular al flujo del calor (en cm$^2$), $T$ es la temperatura (en $^o$C) y $r$ es la distancia (en cm).

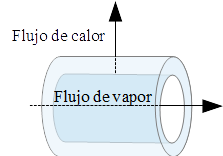
Por una tubería de sección transversal circular por la que está circulando vapor, el flujo de calor es perpendicular al flujo de vapor. Supondremos tanto simetría axial como radial. Si tomamos una porción de tubería de 1 cm de longitud, el área de la superficie para un radio $r$ es $2\pi r$. La variable $r$ varía desde el radio interno (sea $r_0$) hasta el radio externo; llamaremos $T_0$ a la temperatura del vapor en $r_0$, es decir, en la pared interna del tubo. Si la tasa de flujo, $H$, y el coeficiente $k$ de conductividad térmica son conocidos, la ecuación anterior modela la distribución de temperatura hacia el exterior de la pared de esa parte del tubo: $$\frac{dT}{dr}=\frac{H}{2\pi r k}$$ junto con la condición $T=T_0$ en $r=r_0$.

Vaciado de un depósito

El objetivo en este tipo de problemas suele ser establecer un modelo para el nivel de líquido de un depósito con un orificio de salida en su fondo. Para ello utilizamos la expresión del volumen en función de la altura, que dependerá de la forma del depósito, y la ley de Torricelli; esta ley establece que la velocidad de salida del agua por un orificio en el fondo de un depósito es la misma que si cayera libremente desde el nivel del agua hasta el orificio. De esta manera, si llamamos $x(t)$ a la altura de agua en el momento $t$, la velocidad de salida será $$v(t)=\sqrt{2gx(t)}$$ donde $g$ es la aceleración de la gravedad; si $s$ es el área del orificio, la tasa de salida de líquido (o tasa de volumen saliente) es $$s\sqrt{2gx(t)}$$ La razón de cambio del volumen en el depósito es la diferencia entre la tasa de entrada de líquido al depósito y esa tasa de salida.

Caída de un cuerpo

La segunda ley del movimiento de Newton $$\frac{dp}{dt}=F(t,x,\frac{dx}{dt})$$ donde $p(t)=m(t)v(t)$ es la cantidad de movimiento del cuerpo en el instante $t$ y $F(t,x,\frac{dx}{dt})$ es la fuerza resultante de todas las que actúan sobre el cuerpo en el tiempo $t$, en la posición $x$ y a velocidad $\frac{dx}{dt}$.

En la mayoría de las aplicaciones la masa permanece constante, así que la segunda ley de Newton se puede expresar como $$m\frac{dv}{dt}=F(t,x,v(t))$$ que será una ecuación diferencial de primer orden en $v(t)$ siempre que $F$ no dependa de $x$.

Si en el movimiento de caída la masa permanece constante y las únicas fuerzas que actúan sobre el objeto son la gravedad y la resistencia del aire, supuesta proporcional a la velocidad, esta ecuación será $$m\frac{dv}{dt}=mg-kv(t)$$