Un número complejo queda determinado por dos componentes, primera y segunda si está escrito en cartesianas o parte real e imaginaria si lo está en forma binómica. Estas formas de escribir un complejo se basan en el sistema de referencia cartesiano en el plano. Hay otros modos de representar un complejo, basadas también en dos medidas que trataremos en esta sección: el módulo y el argumento.

Módulo de un complejo

El módulo de $z=(a,b)$ es $$|z|=\sqrt{z\overline{z}}=\sqrt{a^2+b^2}$$

• Si $z$ cumple que $\mbox{Im}\, z=0$ (se trata por tanto de un número real), su módulo coincide con su valor absoluto: $|a+0i|=|a|$

• Si $z$ cumple que $\mbox{Re}\, z=0$ (se trata por tanto de un número imaginario), su módulo coincide con el valor absoluto de la parte imaginaria: $|0+bi|=|b|$

• El módulo de $z$ es la distancia de $z$ al origen de coordenadas. Todos los puntos de la circunferencia de centro $(0,0)$ y radio $R$ son afijos de complejos del mismo módulo, $R$. Y viceversa, todos los complejos que tienen cierto módulo, $R$, están en la circunferencia de centro $(0,0)$ y radio $R$.

Módulo como distancia

Igual que $|z|$ es la distancia de $z$ al $(0,0)$, para un complejo dado $z_0$, el número $|z-z_0|$ es la distancia entre los afijos de $z$ y $z_0$: si $z_0=(x_0,y_0)$ y $z=(x,y)$, $$|z-z_0|=\sqrt{(x-x_0)^2+(y-y_0)^2}$$ Los complejos $z$ tales que $|z-z_0|=R$ forman la circunferencia de centro $z_0$ y radio $R$.

Argumento de un complejo

Si el punto $P$ del plano es el afijo del complejo $z$, el ángulo medido en radianes que forma el vector $OP$ con el eje real positivo se llama argumento del número complejo $z$ y se denota por $\mbox{arg}\,z$: $$\cos \varphi=\frac{\mbox{Re}\, z}{|z|}\hspace{.2cm},\hspace{.2cm} \mbox{sen}\, \varphi=\frac{\mbox{Im}\, z}{|z|}$$

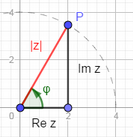
Llamaremos valor principal del argumento al comprendido entre $-\pi$ y $\pi$: $$-\pi < \mbox{arg}\, z\leq \pi$$

Determinaciones del argumento

Hay infinitos ángulos que cumplen estas dos condiciones, $$\cos \varphi=\frac{\mbox{Re}\, z}{|z|}\hspace{.2cm},\hspace{.2cm} \mbox{sen}\, \varphi=\frac{\mbox{Im}\, z}{|z|}$$ cualquiera que resulte de sumar al argumento en valor principal, $\varphi$, un múltiplo entero de $2\pi$ (número entero de vueltas completas): $$\ldots\ \varphi-4\pi\ \ ,\ \ \varphi-2\pi\ \ ,\ \ \varphi+2\pi\ \ ,\ \ \varphi+4\pi\ \ldots$$ Elegir un intervalo de longitud $2\pi$ donde tomar el argumento es elegir una determinación del argumento. Las más habituales son $(-\pi,\pi]$ (determinación principal) o $[0,2\pi)$.

Si un ángulo está entre 0 y $\pi$, se encuentra tanto en la determinación $[0,2\pi)$ como en la $(-\pi,\pi]$. Si en cambio está entre $\pi$ y $2\pi$, se encuentra en la determinación $[0,2\pi)$ pero no en la $(-\pi,\pi]$; para pasarlo a ésta determinación (y ponerlo así en valor principal), debemos restarle $2\pi$. Por ejemplo,

$\frac{7\pi}{4}$ en valor principal es $\frac{-\pi}{4}$, $\frac{11\pi}{6}$ en valor principal es $\frac{-\pi}{6}$, $\frac{4\pi}{3}$ en valor principal es $\frac{-2\pi}{3}$, $\frac{7\pi}{6}$ en valor principal es $\frac{-5\pi}{6}$, $\ldots$

Uso de la función arcotangente

La ventaja de utilizar el valor principal del argumento es que los complejos situados en el semiplano $y>0$ (parte imaginaria positiva) tendrán argumento positivo mientras que los situados en el semiplano $y<0$ (parte imaginaria negativa) tendrán argumento negativo. Eso es útil a la hora de utilizar la arcotangente para hallar el argumento, pues $$\left.\begin{array}{l}\cos \varphi=\frac{\mbox{Re}\, z}{|z|}\\ \mbox{sen}\, \varphi=\frac{\mbox{Im}\, z}{|z|}\end{array}\right\}\ \Rightarrow\ \ \begin{array}{l} \varphi=\mbox{arctg}\frac{\mbox{Im}\, z}{\mbox{Re}\, z}\\ \\ \mbox{signo}(\varphi)=\mbox{signo}(\mbox{Im}\, z)\end{array}$$

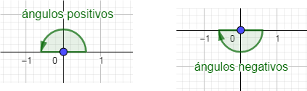
Recuerda que hay dos ángulos entre $-\pi$ y $\pi$ con la misma tangente:

• uno en el primer cuadrante y otro en el tercero si $\frac{\mbox{Im}\, z}{\mbox{Re}\, z}$ es positivo

• uno en el segundo cuadrante y otro en el cuarto si $\frac{\mbox{Im}\, z}{\mbox{Re}\, z}$ es negativo

Sobre todo si utilizas la calculadora debes fijarte en el signo de la parte imaginaria para saber cuál es el correcto en cada caso.