Fórmula de Euler y expresiones de un complejo
Fórmula de Euler
Para cualquier $x$ real se cumple que $$e^{ix}=\cos x+i\mbox{sen}\, x$$ El complejo $\cos x+i\mbox{sen}\, x$ tiene módulo 1 $$|\cos x+i\mbox{sen}\, x|=\sqrt{\cos^2 x+\mbox{sen}^2 x}=1$$ es decir, está en la circunferencia de centro $(0,0)$ y radio 1, y viceversa, cualquier punto de esa circunferencia es de la forma $P(\cos x,\mbox{sen}\, x)$ siendo $x$ el ángulo que forma del segmento $OP$ con el semieje positivo. Por ejemplo, $$e^{i\pi/4}=\cos\frac{\pi}{4}+i\mbox{sen}\frac{\pi}{4}=\frac{\sqrt{2}}{2}(1+i)$$ $$e^{i\pi/2}=\cos\frac{\pi}{2}+i\mbox{sen}\frac{\pi}{2}=i$$ $$e^{i3\pi/4}=\cos\frac{3\pi}{4}+i\mbox{sen}\frac{3\pi}{4}=\frac{\sqrt{2}}{2}(-1+i)$$ $$e^{i\pi}=\cos\pi+i\mbox{sen}\,\pi=-1$$ $$e^{-i\pi/4}=\cos\frac{-\pi}{4}+i\mbox{sen}\frac{-\pi}{4}=\frac{\sqrt{2}}{2}(1-i)$$ $$e^{-i\pi/2}=\cos\frac{-\pi}{2}+i\mbox{sen}\frac{-\pi}{2}=-i$$ $$e^{-i3\pi/4}=\cos\frac{-3\pi}{4}+i\mbox{sen}\frac{-3\pi}{4}=-\frac{\sqrt{2}}{2}(1+i)$$
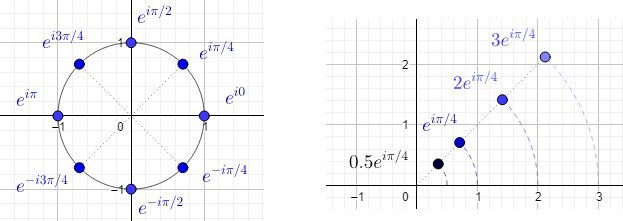
En la figura de la izquierda vemos representados los afijos de esos ocho complejos, todos ellos situados en la circunferencia de radio 1 y centro $(0,0)$, como corresponde a complejos de módulo 1. En la figura de la derecha vemos el efecto de multiplicar un número por una constante positiva. Si la constante fuera negativa, estaríamos sumando $\pi$ al argumento inicial.
OBSERVACIÓN: Todas las expresiones de la forma $e^{(x+2k\pi)i}$ representan al mismo número sea cual sea $k$ entero, pues $$e^{(x+2k\pi)i}=\cos (x+2k\pi)+i\mbox{sen} (x+2k\pi)=\cos x+i\mbox{sen}\, x$$
Forma polar, trigonométrica y exponencial
Con frecuencia es recomendable expresar los complejos utilizando su módulo y su argumento. Si $|z|=r$ y $\varphi=\mbox{arg}\,z$, tenemos varias alternativas para escribir $z$:
Forma polar: $z=r_\varphi$
Forma trigonométrica: $z=r(\cos\varphi+i\,\mbox{sen}\,\varphi)$
Forma exponencial: $z=re^{i\varphi}$