Conjunto de números complejos

Se denota por ${\bf C}$ y es el conjunto $${\bf R}^2=\{(a,b)\, /\, a,\, b\in{\bf R}\}$$ con las operaciones suma y producto siguientes $$(a,b)+(c,d)=(a+c,b+d)$$ $$(a,b)(c,d)=(ac-bd,ad+bc)$$

Afijo de un complejo

El afijo del complejo $(a,b)$ es el punto del plano de coordenadas $(a,b)$. Los afijos de los complejos de la forma $(a,0)$ forman el eje $0X$ y los afijos de los complejos de la forma $(0,b)$ forman el eje $0Y$. Con frecuencia asimilamos el complejo a su afijo, refiriéndonos al complejo cuando hablamos del afijo.

IMPORTANTE: Los números reales pueden ordenarse, se identifican con puntos en una recta. En los números complejos, que se identifican con puntos del plano, no es posible establecer un orden total entre ellos.

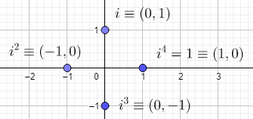
Unidad imaginaria y sus potencias

Es el complejo $(0,1)$ y se denota por $i$ o por $j$. Siguiendo la fórmula para multiplicar complejos, tendremos que $$i^2=(0,1)(0,1)=(-1,0)$$ y puesto que un número complejo de la forma $(a,0)$ es el número real $a$, tendremos $i^2=-1$. Cada complejo $(0,b)$ se expresa como $bi$. Las potencias naturales de $i$ repiten siempre los cuatro valores: $i$, $-1$, $-i$ y 1 ya que $$i^1=i\ ,\ i^2=-1\ ,\ i^3=-i\ , \ i^4=1$$

Introducir la unidad imagina permite escribir los complejos como binomios, lo que resulta una ventaja en muchas de las operaciones.

Forma binómica

Puesto que $(a,b)=(a,0)+(0,b)$, el complejo $z=(a,b)$ se representa en forma binómica como $z=a+bi$.

Conjugado de un complejo

El conjugado del número complejo $z=a+bi$ es $$\overline{z}=a-bi$$ Verifica las siguientes propiedades

• $\overline{\overline{z}}=z$

• $\overline{z+w}=\overline{z}+\overline{w}$

• $\overline{zw}=\overline{z}\,\overline{w}$

• $z\overline{z}$ es un número real positivo: $z\overline{z}=a^2+b^2$

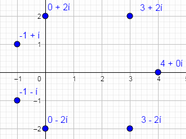
Geométricamente, el afijo de un complejo y el de su conjugado son simétricos respecto del eje $0X$. Así como el producto de un número complejo no nulo por sí mismo es siempre un número real positivo, igualmente la suma de un número complejo con su conjugado es también un número real. Por ejemplo la suma de $-1+i$ con su conjugado es $-2$. Si lo que hacemos es restar un número y su conjugado, entonces se obtendrá un número imaginario (parte real nula); por ejemplo la resta de $-1+i$ y su conjugado es $2i$.

Partes real e imaginaria

La parte real de $z=a+bi$ es $a$ y su parte imaginaria es $b$. Se denotan por $$a=\mbox{Re}\, z \hspace{.2cm}, \hspace{.2cm} b=\mbox{Im}\, z$$ se pueden expresar utilizando el conjugado: $$\mbox{Re}\, z=\frac{z+\overline{z}}{2}\hspace{.2cm}, \hspace{.2cm}\mbox{Im}\, z=\frac{z-\overline{z}}{2i}$$