Ejercicios preliminares e instantáneos. Integral de línea (segunda parte)
Ejercicio 1
Observa que los arcos
$$a) \hspace{.3cm}\left\{ \begin{array}{l} x=t \\ y=t^2\end{array} \right. \hspace{.3cm}t\in [0,1]
\hspace{.3cm}, \hspace{.3cm}
b) \hspace{.3cm} \left\{ \begin{array}{l} x=1-t \\ y=(1-t)^2\end{array} \right. \hspace{.3cm} t\in [0,1]$$
tienen orientación opuesta. Encuentra para cada uno la expresión del vector tangente unitario, ${\bf T}(t)$. Dibuja los correspondientes a $t=0$, $t=1/2$ y $t=1$.
Pista
Solución
Dos curvas tienen orientaciones opuestas si ocupan el mismo lugar geométrico del plano o del espacio y en cada punto los vectores tangentes tienen signo opuesto.
$(t,t^2)$ para $t\in[0,1]$ recorre los puntos de la parábola $y=x^2$ desde el punto $(0,0)$ hasta el punto $(1,1)$, mientras que $(1-t,(1-t)^2)$ con $t\in[0,1]$ recorre los mismos puntos pero empezando en el $(1,1)$ y terminando en el $(0,0)$. Podemos comprobar que los vectores tangentes tienen signos opuestos:
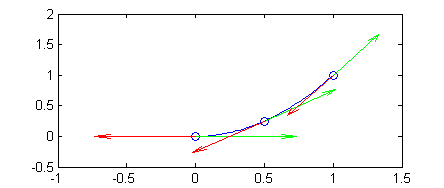

- en $P(0,0)$, los vectores tangentes son $(1,0)$ y $(-1,0)$
- en $P(\frac{1}{2},\frac{1}{4})$, los vectores tangentes son $\frac{1}{\sqrt{2}}(1,1)$ y $-\frac{1}{\sqrt{2}}(1,1)$
- en $P(1,1)$, los vectores tangentes son $\frac{1}{\sqrt{5}}(1,2)$ y $-\frac{1}{\sqrt{5}}(1,2)$
Ejercicio 2
Encuentra ${\bf F}(x(t),y(t))$ siendo ${\bf F}(x,y)=(x^2+y, -1)$ y $(x(t),y(t))$ las coordenadas dadas por
- ${\bf r}(t)=(x(t),y(t))=(2t, t^2-1)$
- ${\bf r}(t)=(x(t),y(t))=(\cos t, 2\,\mbox{sen}\, t)$
- ${\bf r}(t)=(x(t),y(t))=(1-t, 2)$
Comentario
Solución
${\bf F}(x,y)$ es una magnitud vectorial, como un campo de fuerzas o de velocidades, definida en una región del plano y $(x(t),y(t))$ son las coordenadas de un alambre plano situado en esa región; el resultado de componerlas es una función vectorial, de dimensión dos, de una variable.
- ${\bf F}(x(t),y(t))=(5t^2-1,-1)$;
- ${\bf F}(x(t),y(t))=(\cos^2 t+2\,\mbox{sen}\, t,-1)$;
- ${\bf F}(x(t),y(t))=((1-t)^2+2,-1)$
Ejercicio 3
Encuentra ${\bf F}(x(t),y(t),z(t))$ siendo ${\bf F}(x,y,z)=(-z,x+y, x)$ y $(x(t),y(t),z(t))$ las coordenadas dadas por
- ${\bf r}(t)=(x(t),y(t),z(t))=(2t, t^2, t^3)$
- ${\bf r}(t)=(x(t),y(t),z(t))=(t, e^t, t+1)$
- ${\bf r}(t)=(x(t),y(t),z(t))=(\mbox{sen}\, t, \cos t, \mbox{sen}\, 2t)$
Comentario
Solución
${\bf F}(x,y,z)$ es una magnitud vectorial, como un campo de fuerzas o de velocidades, definida en una región del espacio y $(x(t),y(t),z(t))$ son las coordenadas de un alambre situado en esa región; el resultado de componerlas es una función vectorial, de dimensión tres, de una variable.
- ${\bf F}({\bf r}(t))=(-t^3,2t+t^2,2t)$;
- ${\bf F}({\bf r}(t))=(-t-1,t+e^t,t)$;
- ${\bf F}({\bf r}(t))=(-\mbox{sen}\, 2t,\mbox{sen}\, t+\cos t,\mbox{sen}\, t)$.
Ejercicio 4
Determina el elemento diferencial $d{\bf r}=(dx,dy,dz)=(x'(t),y'(t),z'(t))\, dt$ para cada una de la curvas siguientes:
- ${\bf r}(t)=(x(t),y(t),z(t))=(2t, t^2, t^3)$
- ${\bf r}(t)=(x(t),y(t),z(t))=(t, e^t, t+1)$
- ${\bf r}(t)=(x(t),y(t),z(t))=(\mbox{sen}\, t, \cos t, \mbox{sen}\, 2t)$
Pista
Solución
El elemento diferencial de curva, $d{\bf r}$, es un función vectorial formada por los diferenciales de cada componente de la curva.
- $d{\bf r}=(2,2t,3t^2)\, dt$;
- $d{\bf r}=(1,e^t,1)\, dt$;
- $d{\bf r}=(\cos t,-\mbox{sen}\, t,2\cos 2t)\, dt$.
Ejercicio 5
Si ${\bf V}(x,y,z)$ es el vector de velocidades (en m/sg) de una partícula moviéndose por la curva $C$ dada por ${\bf r}(t)=(x(t),y(t),z(t))$ (las longitudes medidas en m.), indica en qué unidades se mide
- $d{\bf r}=(dx,dy,dz)$
- ${\bf V}\cdot d{\bf r}$
- $\int_C {\bf V}\cdot d{\bf r}$
Pista
Solución
Recuerda que podemos interpretar la diferencial de una variable como una diferencia entre valores de esa variable.
- $d{\bf r}=(dx,dy,dz)$ se mide en (m.,m.,m.);
- ${\bf V}\cdot d{\bf r}$ se mide en $\mbox{m}^2/\mbox{sg}$ pues es un flujo;
- $\int_C {\bf V}\cdot d{\bf r}$ se mide en $\mbox{m}^2/\mbox{sg}$ pues es un flujo.
Ejercicio 6
Indica cuáles de las siguientes curvas planas son cerradas:
- ${\bf r}(t)=(1+\,\mbox{sen}\, t,\cos t)$ para $t\in[0,2\pi]$
- $y=1-x^2$ para $x\in[-1,1]$
- arco unión de $y=1-x^2$ con $y=x^2-1$ para $x\in[-1,1]$
- $2x^2+3y^2=8$ para $x\in[-2,2]$
Pista
Solución
De cara a aplicar el teorema de Green, es imprescindible saber si la curva es cerrada o no lo es. Para saber si una curva es cerrada no es necesario dibujarla; basta comprobar que el punto correspondiente al primer valor del parámetro es el mismo que el correspondiente al último valor del parámetro. (En un caso más complicado podría ser que el punto fuera el mismo para un valor intermedio y a partir de éste hasta el final del intervalo se repitieran los mismos puntos)
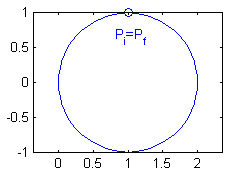
- ${\bf r}(t)=(1+\,\mbox{sen}\, t,\cos t)$ para $t\in[0,2\pi]$: puesto que ${\bf r}(0)={\bf r}(2\pi)$, la curva es cerrada:
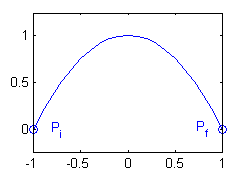
- $y=1-x^2$ para $x\in[-1,1]$: el punto inicial es $(-1,0)$ y el final $(1,0)$, luego no es cerrada:
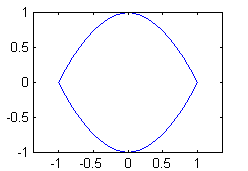
- arco unión de $y=1-x^2$ con $y=x^2-1$ para $x\in[-1,1]$: cada uno de los arcos no es cerrado, pero sí su unión:
- $2x^2+3y^2=8$ para $x\in[-2,2]$: si el punto inicial es $(-2,0)$, éste es también el punto final:
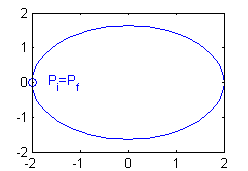
Ejercicio 7
En cada caso, sombrea la región encerrada entre las curvas que se indican
- circunferencias $x^2+y^2=1$, $x^2+y^2=2$, sobre la recta $2y=-x$;
- parábola $(x-1)^2=2-y$ y eje $y=0$;
- parábola $(x-1)^2=2-y$ y recta $3y=2x-6$.
Solución
- circunferencias $x^2+y^2=1$, $x^2+y^2=2$, sobre la recta $2y=-x$:
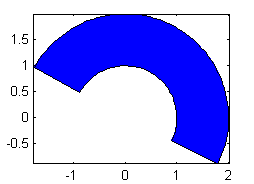
a=atan(-.5); t=a:.05:a+pi; tv=t(end:-1:1); fill([cos(t) 2*cos(tv)],[sin(t) 2*sin(tv)],'b') axis equal
- parábola $(x-1)^2=2-y$ y eje $y=0$:
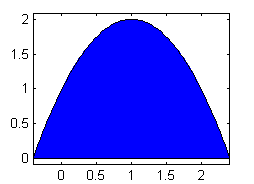
x=1-sqrt(2):sqrt(2)/40:1+sqrt(2); fill(x,2-(x-1).^2,'b') axis equal
- parábola $(x-1)^2=2-y$ y recta $3y=2x-6$:
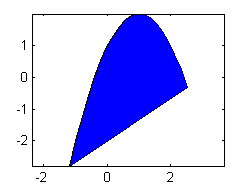
[x,y] = solve('(x-1)^2=2-y','3*y=2*x-6'); x=double(x); xv=linspace(min(x),max(x),20); fill(xv,2-(xv-1).^2,'b') axis equal
Ejercicio 8
Analiza si la orientación de las siguientes curvas planas cerradas es positiva o negativa, en ambos casos $t\in[0,2\pi]$:
$$ \mbox{a)}\hspace{.3cm} {\bf r}(t)=(\mbox{sen}\, t,\cos t) \hspace{1cm} \mbox{b)}\hspace{.3cm}{\bf r}(t)=(1+\cos t,2-\,\mbox{sen}\, t)$$
Pista
Solución
Recuerda que en una curva plana se considera orientación positiva la orientación antihoraria.
Ambas tienen orientación negativa:
- para $t=0$, el punto es $P(0,1)$; para $t=\frac{\pi}{2}$, el punto es $Q(1,0)$;
- para $t=0$, el punto es $P(2,2)$; para $t=\frac{\pi}{2}$, el punto es $Q(1,1)$;
Ejercicio 9
Encuentra la expresión de la función $N'_x-M'_y$ para
- $${\bf F}(x,y)=M(x,y)\,{\bf i}+N(x,y)\,{\bf j}=(3x^2-xy)\,{\bf i}+\mbox{arctg}\frac{y}{x}\,{\bf j}$$
- $${\bf F}(x,y)=(M(x,y),N(x,y))=(\mbox{sen}\, (xy), \frac{xy}{x+1})$$
Comentario
Solución
Esta combinación de parciales es importante porque es la función de dos variables que se integra en el interior de una curva cerrada cuando aplicamos el teorema de Green. Es la función que es nula si el campo es conservativo.
- $$N'_x-M'_y=\frac{-y}{x^2+y^2}+x$$
- $$N'_x-M'_y=\frac{y^2}{(x+y)^2}-x\cos (xy)$$