Ejercicios preliminares e instantáneos. Integral de línea (primera parte)
Ejercicio 1
- Determina cuáles de los siguientes lugares geométricos son curvas y en caso afirmativo analiza si son cerradas. Las que sean curvas dibújalas después en el ordenador.
- puntos imagen de ${\bf r}(t)=(\cos t, \mbox{sen}\, t)$, para $t\in[0,2\pi]$
- puntos imagen de ${\bf r}(t)=(\cos t, \mbox{sen}\, t,t)$, para $t\in[0,2\pi]$
- puntos imagen de ${\bf r}(u,v)=(\cos u, \mbox{sen}\, u,v)$, para $u\in[0,2\pi]$ y $v\in[0,1]$
- intersección de $x^2+y^2=1$ con $x+y+z=2$
- intersección de $z=x^2+y^2$ con $z=0$
- proyección de $z=1-(x^2+y^2)$ en el plano $z=0$
- proyección de $x^2+z^2=4$ en el plano $y=0$
Pista
Solución
Recuerda que una curva es la imagen de una función de una única variable. Para movernos por ella sólo tenemos un grado de libertad.
- ${\bf r}(t)=(\cos t, \mbox{sen}\, t)$, para $t\in[0,2\pi]$ es la circunferencia de centro $(0,0)$ y radio 1, por tanto es una curva cerrada. La dibujamos con
t=0:pi/50:2*pi; plot(cos(t),sin(t)) axis equal
- ${\bf r}(t)=(\cos t, \mbox{sen}\, t,t)$, para $t\in[0,2\pi]$ es una espira de hélice, por tanto es una curva no cerrada. La dibujamos con
t=0:pi/50:2*pi; plot3(cos(t),sin(t),t) grid on axis equal
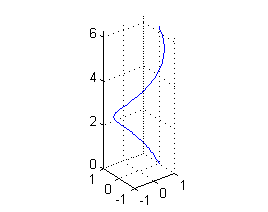
- ${\bf r}(u,v)=(\cos u, \mbox{sen}\, u,v)$, para $u\in[0,2\pi]$ y $v\in[0,1]$ es una porción de superficie;
- $x^2+y^2=1$ interseca a $x+y+z=2$ en una curva cerrada, que podríamos parametrizar con $(\cos t,\mbox{sen}\, t,2-\cos t-\mbox{sen}\, t)$, $t\in[0,2\pi]$ y dibujarla con
t=0:pi/50:2*pi; plot3(cos(t),sin(t),2-cos(t)-sin(t)) grid on axis equal
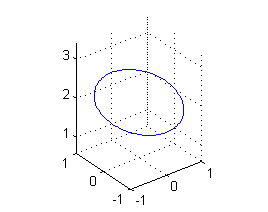
- $z=x^2+y^2$ sólo interseca a $z=0$ en el punto $(0,0,0)$;
- la proyección de $z=1-(x^2+y^2)$ en el plano $z=0$ es un disco, no una curva;
- la proyección de $x^2+z^2=4$ en el plano $y=0$ es la circunferencia de centro $(0,0,0)$ y radio 2, por tanto curva cerrada, que podríamos parametrizar con $(2\cos t,0,2\,\mbox{sen}\, t)$, $t\in[0,2\pi]$ y dibujarla con
t=0:pi/50:2*pi; plot3(2*cos(t),zeros(size(t)),2*sin(t)) grid on axis equal
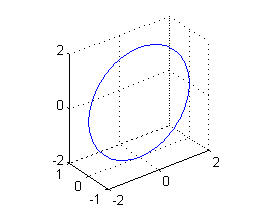
Ejercicio 2
Comprueba que las dos parametrizaciones siguientes lo son del mismo arco ($x^2+y=3$, para $1<x<2$):
$$\left\{ \begin{array}{l} x(t)=\frac{t}{2} \\ y(t)=3-\frac{t^2}{4} \end{array}\right.
\ \ ,\ \ 2<t<4
\hspace{1cm} ; \hspace{1cm} \left\{ \begin{array}{l} x(u)=\sqrt{3-u} \\ y(u)=u \end{array}\right.
\ \ ,\ \ -1<u<2$$
Pista
Debes comprobar que en ambos casos la primera coordenada está entre 1 y 2 y que la suma del cuadrado de la primera con la segunda vale 3.
Ejercicio 3
En cada caso, encuentra el valor de $t$ para el cual ${\bf r}(t)=(2t^2,2+\cos t)$ es el vector de posición de
- $A(0,3)$
- $B(\frac{\pi^2}{2},2)$
- $C(9\frac{\pi^2}{2},2)$
- $D(2\pi^2,1)$
Solución
- $t=0$ pues ${\bf r}(0)=(0,3)$;
- $t=\frac{\pi}{2}$ pues ${\bf r}(\frac{\pi}{2})=(\frac{\pi^2}{2},2)$;
- $t=\frac{3\pi}{2}$ pues ${\bf r}(\frac{3\pi}{2})=(9\frac{\pi^2}{2},2)$;
- $t=\pi$ pues ${\bf r}(\pi)=(2\pi^2,1)$
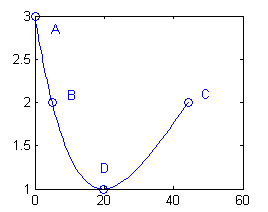
t=0:pi/50:3*pi/2; plot(2*t.^2,2+cos(t)) hold on t=0:pi/2:3*pi/2; plot(2*t.^2,2+cos(t),'o') hold off
Ejercicio 4
¿Cuáles de los siguientes son puntos del arco dado por ${\bf r}(t)=(1+\cos t)\, {\bf i}+(\mbox{sen}\, 2t) \, {\bf j}$? Después de averiguarlo, dibuja el arco y los puntos en el ordenador.
- $A(2,0)$
- $B(1,1)$
- $C(0,1)$
- $O(0,0)$
- $D(1,0)$
Solución
- sí, para $t=0$;
- no;
- no;
- sí, para $t=\pi$;
- sí, para $t=\pi/2$.
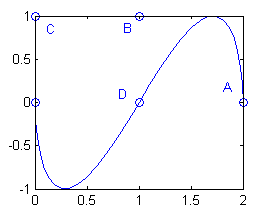
t=0:pi/30:pi; plot(1+cos(t),sin(2*t)) hold on plot([2,1,0,0,1],[0,1,1,0,0],'o') hold off
Ejercicio 5
Para cada ${\bf r}(t)$, halla el vector tangente, ${\bf r'}(t)$, en el punto correspondiente al valor de $t$ indicado; representa a mano esos vectores tangentes y calcula los correspondientes vectores ${\bf T}(t)$ (normaliza a uno el vector ${\bf r'}(t)$); por último dibuja un arco de la curva y el vector tangente calculado en el ordenador:
- ${\bf r}(t)=(\cos 2t, 1+\mbox{sen}\, t)$, $t=0$
- ${\bf r}(t)=(t\,\mbox{sen}\, t, t^2)$, $t=\pi/2$
- ${\bf r}(t)=(\log t, 2t-1)$, $t=1$
Pista
Solución
Recuerda que la derivada de ${\bf r}(t)=(x(t),y(t))$ es ${\bf r'}(t)=(x'(t),y'(t))$.
- Si ${\bf r}(t)=(\cos 2t, 1+\mbox{sen}\, t)$,
$${\bf r'}(0)=(x'(0),y'(0))=(0,1)$$ y $${\bf T}(0)=(0,1)$$
es el vector tangente unitario en el punto $P(1,1)$
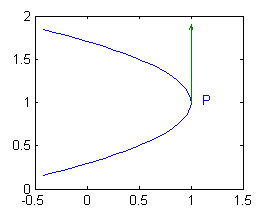
t=-1:.05:1; plot(cos(2*t),1+sin(t)) hold on quiver(1,1,0,1) hold off
- Si ${\bf r}(t)=(t\,\mbox{sen}\, t, t^2)$,
$${\bf r'}\left(\frac{\pi}{2}\right )=\left(x'\left(\frac{\pi}{2}\right),y'\left(\frac{\pi}{2}\right ) \right )=(1,\pi)$$ y $${\bf T}\left(\frac{\pi}{2} \right )=\frac{1}{\sqrt{1+\pi^2}}(1,\pi)$$ es el vector tangente unitario en $P(\frac{\pi}{2},\frac{\pi^2}{4})$
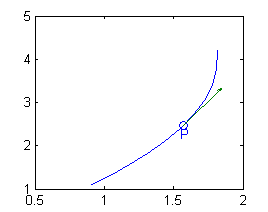
t=pi/3:.1:2*pi/3; plot(t.*sin(t),t.^2) hold on plot(pi/2,pi^2/4,'o') quiver(pi/2,pi^2/4,1/sqrt(1+pi^2),pi/sqrt(1+pi^2)) hold off
- Si ${\bf r}(t)=(\log t, 2t-1)$
$${\bf r'}(1)=(x'(1),y'(1))=(1,2)$$ y $${\bf T}(1)=\frac{\sqrt{5}}{5}(1,2)$$ es el vector tangente unitario en $P(0,1)$
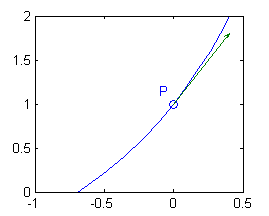
t=.5:.1:1.5; plot(log(t),2*t-1) hold on plot(0,1,'o') quiver(0,1,1/sqrt(5),2/sqrt(5)) hold off
Ejercicio 6
Para las mismas curvas y mismos puntos del ejercicio anterior, encuentra un vector normal unitario (en cada punto, podrá elegirse entre dos sentidos para la dirección normal):
- ${\bf r}(t)=(\cos 2t, 1+\mbox{sen}\, t)$, $t=0$
- ${\bf r}(t)=(t\,\mbox{sen}\, t, t^2)$, $t=\pi/2$
- ${\bf r}(t)=(\log t, 2t-1)$, $t=1$
Pista
Solución
Recuerda que dos vectores son normales si su producto escalar es nulo. De manera que tanto $(u_2,-u_1)$ como $(-u_2,u_1))$ son normales a $(u_1,u_2)$. Si este vector es de módulo 1, también $(u_2,-u_1)$ y $(-u_2,u_1)$ lo son.
- ${\bf n}(0)=(1,0)$
- ${\bf n}(\frac{\pi}{2})=\frac{1}{\sqrt{1+\pi^2}}(\pi,-1)$
- ${\bf n}(1)=\frac{\sqrt{5}}{5}(-2,1)$
Ejercicio 7
Si $t$ se mide en segundos (sg.) y $x(t)$, $y(t)$ y $\rho(\theta)$ en milímetros (mm.), indica en qué unidades se miden
- $x'(t)$ e $y'(t)$
- $\sqrt{x'(t)^2+y'(t)^2}$
- $ds=\sqrt{x'(t)^2+y'(t)^2}\, dt$
- $\rho'(\theta)$
- $\sqrt{\rho(\theta)^2+\rho'(\theta)^2}$
- $ds=\sqrt{\rho(\theta)^2+\rho'(\theta)^2}\, d\theta$
Pista
Solución
Recuerda que la derivada es el límite de un cociente, luego su dimensión será el cociente de las dimensiones de la variable que se deriva entre la variable respecto de la que se deriva; la diferencial de una variable no es más que una diferencia entre valores de esa variable; por lo tanto si, por ejemplo, la variable es una longitud, su diferencial también lo será.
- $x'(t)$ e $y'(t)$ se miden en mm/sg;
- $\sqrt{x'(t)^2+y'(t)^2}$ se mide en mm/sg;
- $ds=\sqrt{x'(t)^2+y'(t)^2}\, dt$ se mide en mm;
- $\rho'(\theta)$ se mide en mm;
- $\sqrt{\rho(\theta)^2+\rho'(\theta)^2}$ se mide en mm;
- $ds=\sqrt{\rho(\theta)^2+\rho'(\theta)^2}\, d\theta$ se mide en mm.
Ejercicio 8
Analiza la suavidad de los arcos de curva siguientes
- ${\bf r}(t)=(\cos t, t^2)$, $t\in [-1,1]$
- ${\bf r}(t)=(\cos t, \mbox{sen}\, t)$, $t\in [-1,1]$
- ${\bf r}(t)=(\log t, t^2,t)$, $t\in [1,2]$
Pista
Solución
Recuerda que una curva $(x(t),y(t))$ es suave en un punto $(x(t_0),y(t_0))$ si $x'(t_0)^2+y'(t_0)^2\neq 0$, de manera que está garantizada la existencia de vector tangente a la curva en ese punto.
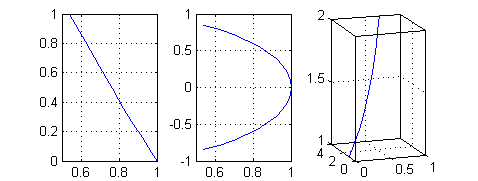
- ${\bf r}(t)=(\cos t, t^2)$ es suave en todos los puntos de $[-1,1]$ salvo en ${\bf r}(0)$, que es el punto $P(1,0)$;
- ${\bf r}(t)=(\cos t, \mbox{sen}\, t)$ es suave en todos sus puntos;
- ${\bf r}(t)=(\log t, t^2,t)$, $t\in [1,2]$ es suave.
t=-1:.1:1; subplot(1,3,1); plot(cos(t),t.^2);grid on subplot(1,3,2); plot(cos(t),sin(t));grid on t=1:.1:2; subplot(1,3,3); plot3(log(t),t.^2,t) box on grid on
Ejercicio 9
Encuentra $f(x(t),y(t))$ siendo $f(x,y)=x^2+y$ y $(x(t),y(t))$ las coordenadas dadas por
- ${\bf r}(t)=(x(t),y(t))=(2t, t^2-1)$
- ${\bf r}(t)=(x(t),y(t))=(\cos t, 2 \mbox{sen}\, t)$
- ${\bf r}(t)=(x(t),y(t))=(1-t, 2)$
Comentario
Solución
$f(x,y)$ es una magnitud escalar, como la densidad o la temperatura, definida en una cierta región del plano y $(x(t),y(t))$ son las coordenadas de, por ejemplo, un alambre en el plano; el resultado de componerlas es una función, escalar, de una variable.
- $f(x(t),y(t))=5t^2-1$;
- $f(x(t),y(t))=\cos^2 t+2\, \mbox{sen}\, t$;
- $f(x(t),y(t))=t^2-2t+3$
Ejercicio 10
Encuentra $f(x(t),y(t),z(t))$ siendo $f(x,y,z)=xy-z$ y $(x(t),y(t),z(t))$ las coordenadas dadas por
- ${\bf r}(t)=(x(t),y(t),z(t))=(2t, t^2, t^3)$
- ${\bf r}(t)=(x(t),y(t),z(t))=(t, e^t, t+1)$
- ${\bf r}(t)=(x(t),y(t),z(t))=(\mbox{sen}\, t, \cos t, \mbox{sen}\, 2t)$
Comentario
Solución
$f(x,y,z)$ es una magnitud escalar, como la densidad o la temperatura, definida en una cierta región del espacio y $(x(t),y(t),z(t))$ son las coordenadas de, por ejemplo, un alambre situado en esa región del espacio; el resultado de componerlas es una función, escalar, de una variable.
- $f(x(t),y(t),z(t))=t^3$;
- $f(x(t),y(t),z(t))=te^t-(t+1)$;
- $f(x(t),y(t),z(t))=-\mbox{sen}\, t \cos t$
Ejercicio 11
- Divide el intervalo $[0,\pi]$ en seis subintervalos iguales.
- Dibuja el arco $C$ dado por ${\bf r}(t)=(2\cos t, 2\,\mbox{sen}\, t)$, $t\in[0,\pi]$ dividido en los seis subarcos correspondientes.
- Encuentra $\Delta s=|{\bf r}'(t)|\Delta t$ (ten en cuenta que $\Delta t$ es la longitud de cada uno de los subintervalos en que se dividió $[0,\pi]$)
Solución
- $$[0,\pi]=[0,\frac{\pi}{6}]\cup [\frac{\pi}{6},\frac{\pi}{3}]\cup [\frac{\pi}{3},\frac{\pi}{2}]\cup [\frac{\pi}{2},2\frac{\pi}{3}]\cup [2\frac{\pi}{3},5\frac{\pi}{6}]\cup [5\frac{\pi}{6},\pi]$$
-
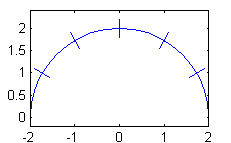
- $|{\bf r'}(t)|=2$ e $\Delta t=\frac{\pi}{6}$, luego $\Delta s=\frac{\pi}{3}$
Ejercicio 12
Continuando con el ejercicio anterior, en el que se dividió el arco
${\bf r}(t)=(2\cos t, 2\,\mbox{sen}\, t)$, $t\in[0,\pi]$ en seis subarcos, toma en cada subarco de $C$ el punto situado más a la izquierda; esos puntos son $(x(t_i),y(t_i))$ para $i=1$ hasta $i=6$; calcula la suma $$\sum_{i=1}^6 f(x(t_i),y(t_i))\Delta s_i$$ para la función $f(x,y)=x-y$.
Solución
Los puntos son $P_1(\sqrt{3},1)$, $P_2(1,\sqrt{3})$, $P_3(0,2)$, $P_4(-1,\sqrt{3})$, $P_5(-\sqrt{3},1)$ y $P_6(-2,0)$:
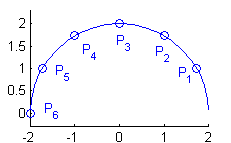

La suma pedida es $-\frac{2\pi}{3}(3+\sqrt{3})$
Ejercicio 13
Si $x$, $y$ y $z$ se miden en cm., $\delta (x,y,z)$ en gr$/$cm y $C$ es una curva, indica en qué unidades se mide
- $\delta (x,y,z)\, ds$
- $I=\int_C \delta (x,y,z)\, ds$
- $\frac{I}{\mbox{longitud}(C)}$
Solución
- $\delta (x,y,z)\, ds$ se mide en gr.;
- $I=\int_C \delta (x,y,z)\, ds$ se mide en gr.;
- $\frac{I}{\mbox{longitud}(C)}$ se mide en gr/cm.
Ejercicio 14
Si $x$, $y$ y $f(x,y)$ se miden en mm., indica en qué unidades se mide
- $f(x,y)\, ds$
- $\int_C f (x,y)\, ds$
Solución
- $f(x,y)\, ds$ se mide en $\mbox{mm}^2$;
- $\int_C f (x,y)\, ds$ se mide en $\mbox{mm}^2$