Longitud de una curva
Si para una curva plana $C$ se integra el campo constante
$f(x,y) = 1$ o si para
la curva en el espacio se integra el campo constante $f(x,y,z) =
1$, se
obtendrá la longitud de $C$.
$${\kern 1pt} longitud{\kern 1pt} (C) = \int_C ds$$
$${\kern 1pt} longitud{\kern 1pt} (C) = \int_C ds$$
Área de una valla
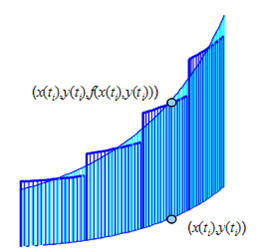
Como se justificó en la interpretación geométrica, el área de la
valla construida sobre una curva plana $C$, con altura $f$ en cada punto, es la
integral $f(x,y)$ de sobre $C$.
Masa y densidad de un alambre
Si $C$ tiene la forma de un alambre, o elemento de una única
dimensión significativa, y el campo $f$ da el valor de la densidad
lineal en cada punto del alambre, es decir $f\left( {x,y,z}
\right) = \delta \left( {x,y,z} \right)$, será
$${\kern 1pt} masa{\kern 1pt} \;total(C) = \int_C \,\delta \left( {x,y,z} \right)\,ds$$
$$densidad\;media(C) = {{\int_C \,\delta \left( {x,y,z} \right)\,ds} \over {\int_C \,ds}}$$
$${\kern 1pt} masa{\kern 1pt} \;total(C) = \int_C \,\delta \left( {x,y,z} \right)\,ds$$
$$densidad\;media(C) = {{\int_C \,\delta \left( {x,y,z} \right)\,ds} \over {\int_C \,ds}}$$
Temperatura media de un alambre
Si $C$ tiene la forma de un alambre, o elemento de una única dimensión
significativa, y el campo $f$ da el valor de la temperatura en cada
punto del alambre, es decir $f\left( {x,y,z} \right) = T\left(
{x,y,z} \right)$, tendremos
$$temperatura\;media(C) = {{\int_C \,T\left( {x,y,z} \right)\,ds} \over {\int_C \,ds}}$$
$$temperatura\;media(C) = {{\int_C \,T\left( {x,y,z} \right)\,ds} \over {\int_C \,ds}}$$
