Enunciado
- Si ${\cal L}[f(t)]=F(s)$ y ${\cal L}[g(t)]=G(s)$, demuestra formalmente (suponiendo que se cumplen las suficientes condiciones para realizar todos los pasos precisos) que
$$\int_0^\infty F(x)g(x)\, dx =\int_0^\infty f(x)G(x)\, dx$$
- Aplica esa propiedad para hallar el valor de $$\int_0^\infty \frac{\mbox{sen}\, ax}{x}\, dx$$
- Elige un valor de $a$ y dibuja para $x\in[0,20]$ las curvas $$y=\frac{\mbox{sen}\, ax}{x} \hspace{.4cm} \mbox{e} \hspace{.4cm} y=\frac{a}{x^2+a^2}$$
Resolución del primer apartado
Para demostrar la expresión del enunciado seguiremos los siguientes pasos:
- Escribimos la definición de $F(x)$
- La sustituimos en el primer miembro de la expresión $\int_0^\infty F(x)g(x)\, dx =\int_0^\infty f(x)G(x)\, dx$
- Cambiamos el orden de la integral doble resultante
- Utilizamos la expresión de la transformada de Laplace de $g(t)$
Ver
Puesto que $$F(x)=\int_0^\infty e^{-xt}f(t)\, dt$$
$$\int_0^\infty F(x)g(x)\, dx = \int_0^\infty\left(\int_0^\infty e^{-xt}f(t)\, dt \right) g(x)\, dx=
\int_0^\infty \int_0^\infty e^{-xt} f(t) g(x)\, dt\, dx=\ldots$$
Cambiando el orden de integración de esta integral doble,
$$\ldots=\int_0^\infty \int_0^\infty e^{-xt} f(t) g(x)\, dx\, dt=
\int_0^\infty f(t) \left(\int_0^\infty e^{-xt}g(x)\, dx \right) dt=\int_0^\infty f(t) G(t)\, dt$$
donde, para llegar a la última expresión, se ha utilizado la definición de transformada aplicada a la función $g(x)$.
Resolución del segundo apartado
Para poder aplicar la propiedad del primer apartado, hemos de buscar $F(x)$ y $g(x)$ que nos permitan escribir $\frac{\mbox{sen}\, ax}{x}$ como el producto $F(x)g(x)$:
$F(x)=\mbox{sen}\, ax$ y $g(x)=\frac{1}{x}$
Ninguna de las dos propuestas es adecuada.
$F(x)=\frac{1}{x}$ y $g(x)=\mbox{sen}\, ax$
Teniendo en cuenta la tabla básica de transformadas, ¿crees que ésa es una buena elección?
Sí hay una apropiada.
En efecto, si $F(x)={\cal L}[f(t)]=\frac{1}{x}$, entonces $f(t)=1$; y si $g(t)=\mbox{sen}\, at$ entonces $G(x)={\cal L}[g(t)]=\frac{a^2}{x^2+a^2}$, luego
$$\int_0^\infty \frac{\mbox{sen}\, ax}{x}\, dx=\int_0^\infty \frac{a^2}{x^2+a^2}\, dx=
\left[\mbox{arctg} \frac{x}{a}\right]_0^\infty=\frac{\pi}{2}$$
Resolución del tercer apartado
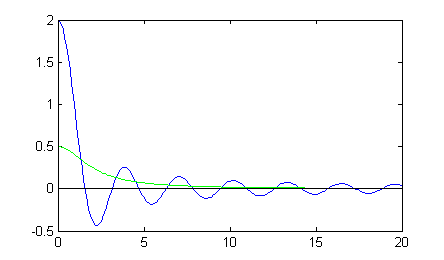
Tomamos aquí $a=2$. Escribe las líneas con las que dibujas las curvas dadas por $$y=\frac{\mbox{sen}\, ax}{x} \hspace{.4cm} \mbox{e} \hspace{.4cm} y=\frac{a}{x^2+a^2}$$ en el ordenador y pulsa en 'Ver'.
Ver
x=0:.1:20; a=2; plot(x,sin(a*x)./x,x,a./(x.^2+a^2),'g',[0,20],[0 0],'k')Donde a las dos gráficas requeridas hemos añadido un eje horizontal en negro (eje $0X$):