Índice de tema

 

Enunciado

  1. Sea $f(t)$ una función definida en $[0,\infty)$, seccionalmente continua y de orden exponencial. Comprueba que si $f(t)$ es $T$-periódica, es decir, si $f(t+T)=f(t)$ para cualquier $t$, entonces $${\cal L}[f(t)]=\frac{1}{1-e^{-Ts}}\int_0^T e^{-st}f(t)\, dt$$
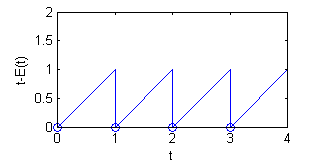
  2. Halla la transformada de Laplace de $f(t)=t-E(t)$, siendo $E(t)$ la función parte entera de $t$.
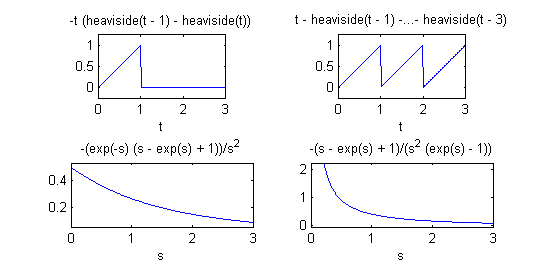
  3. Representa la función $g(t)$ que vale $t$ en $[0,1]$ y cero en el resto; representa también la función $f(t)$ del apartado anterior y las transformadas de Laplace de $f(t)$ y de $g(t)$; dispón las cuatro gráficas en una matriz de gráficos de dimensión 2x2.

Resolución del primer apartado

Paso 1

Escribir la definición de transformada de Laplace de $f(t)$ y expresar la integral como suma de la integral en un periodo y la integral en el resto: $${\cal L}[f(t)]=\int_0^\infty e^{-st} f(t)\, dt=\int_0^T e^{-st} f(t)\, dt+\int_T^\infty e^{-st} f(t)\, dt$$

Paso 2

Realizar un cambio de variable en la segunda de estas integrales que sitúe el intervalo de integración de nuevo entre 0 e infinito. Piensa cuál será ese cambio y pulsa en 'Ver'.
Ver
Si hemos de pasar el extremo izquierdo de $T$ a $0$, tomaremos $$u=t-T$$ y así $$\int_T^\infty e^{-st} f(t)\, dt=\int_0^\infty e^{-s(u+T)}f(u+T) \, du=e^{-sT}\int_0^\infty e^{-su}f(u+T) \, du$$ pero puesto que la función $f$ es $T$-periódica, la última expresión es $$e^{-sT}\int_0^\infty e^{-su}f(u) \, du=e^{-sT}{\cal L}[f]$$ Volviendo a la expresión inicial para ${\cal L}[f]$, $${\cal L}[f(t)]=\int_0^T e^{-st} f(t)\, dt+e^{-sT}{\cal L}[f]$$ de donde despejamos ${\cal L}[f(t)]$, $${\cal L}[f(t)]=\frac{1}{1-e^{-sT}}\int_0^T e^{-st} f(t)\, dt$$

Resolución del segundo apartado

Una opción para encontrar la transformada de $t-E(t)$ es hacer previamente la de $E(t)$ escribiéndola como suma infinita de escalones $U(t-k)$ con $k$ variando en los naturales. Otra opción, que es la que seguiremos aquí, es utilizar el resultado del apartado anterior, puesto que $t-E(t)$ es una función periódica. Analiza de qué periodo y luego pulsa en 'Ver'.
Ver
Observamos que $E(t)$ cumple que $E(t+1)=1+E(t)$

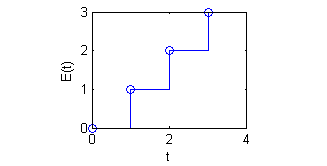
Gráfica

Así que la función $f(t)=t-E(t)$ cumplirá $$f(t+1)=t+1-E(t+1)=t+1-(1+E(t))=t-E(t)=f(t)$$

Gráfica

Por tanto para encontrar su transformada podemos utilizar la propiedad del apartado anterior, ... hazlo tú y pulsa en 'Continuar'.
$${\cal L}[f(t)]=\frac{1}{1-e^{-s}}\int_0^1 e^{-st}f(t)\, dt=\frac{1}{1-e^{-s}}\int_0^1 e^{-st}t\, dt$$ Esta integral la hallamos integrando por partes ($u=t$, $dv=e^{-st}\, dt$). Resulta $$\int_0^1 e^{-st}t\, dt=\frac{1}{s^2}(1-e^{-s})-\frac{e^{-s}}{s}$$ de donde $${\cal L}[f(t)]=\frac{1}{s^2}-\frac{e^{-s}}{s(1-e^{-s})}=\frac{e^s-1-s}{s^2(e^s-1)}\ \ ,\ \ s>0$$

Resolución del tercer apartado

Para dibujar la función $g(t)$, que vale $t$ entre 0 y 1, y se anula en el resto, podemos escribir 
syms t s
figure(1)
subplot(2,2,1)
g=t*(heaviside(t)-heaviside(t-1));
ezplot(g,[0,3])
axis equal
de cuya ejecución se obtiene

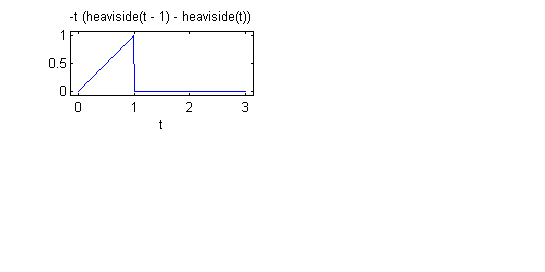
Gráfica

Añade el resto de las líneas necesarias para dibujar las otras tres funciones que se piden en el enunciado. Pulsa en 'Ver' cuando lo tengas.
Ver
El fichero completo sería 
syms t s
figure(1)
subplot(2,2,1)
g=t*(heaviside(t)-heaviside(t-1));
ezplot(g,[0,3])
axis equal
subplot(2,2,2)
f=t-(heaviside(t-1)+heaviside(t-2)+heaviside(t-3));
ezplot(f,[0,3])
axis equal
F=(exp(s)-1-s)/(s^2*(exp(s)-1));
G=(exp(s)-1-s)/(s^2*exp(s));
subplot(2,2,3)
ezplot(G,[0,3])
subplot(2,2,4)
ezplot(F,[0,3])

Gráfica