Ejercicios preliminares e instantáneos. Transformada de Laplace.
Ejercicio 1
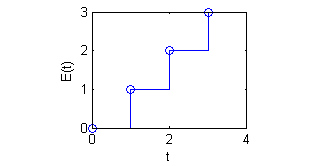
¿Es la función parte entera de $t$ (se suele denotar $E(t)$ y asigna a $t$ el mayor entero menor que $t$) una función seccionalmente continua en $[0,\infty)$?
Pista
Solución
Recuerda que una función es seccionalmente continua en $[0,\infty)$ si lo es en cada intervalo de la forma $[0,A)$, con $A>0$. Una función es seccionalmente continua en un intervalo $[a,b]$ si es continua en todos los puntos de $[a,b]$ salvo quizá en un número finitos de puntos, en los cuales deben existir límites laterales finitos.
$E(t)$ es seccionalmente continua en $[0,\infty)$ pues lo es en cada intervalo de la forma $[0,A)$, con $A>0$: en cada intervalo $[0,A)$, con $A>0$, la función es continua salvo en los enteros menores que $A$, donde la discontinuidad es de salto, existiendo por tanto límites laterales finitos.
Ejercicio 2
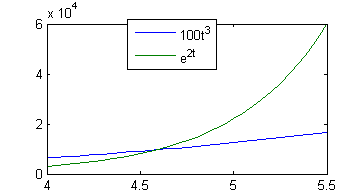
- ¿Existe un valor $t_0$ a partir del cual (es decir, para $t>t_0$) se cumpla que $100\,t^3<e^{2t}$?
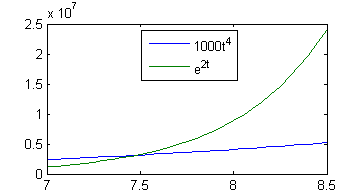
- ¿Y si fuera $1000\, t^4<e^{2t}$?
Solución
- Sí, por ejemplo $t_0=5$;
- Sí, con $t_0=8$.
Ejercicio 3
¿Cuál es el límite de $e^{Ax}$ cuando $x\rightarrow \infty$?
Solución
- Si $A<0$, el límite es 0.
- Si $A=0$, el límite es 1.
- Si $A>0$, el límite es $\infty$.
Por ejemplo:
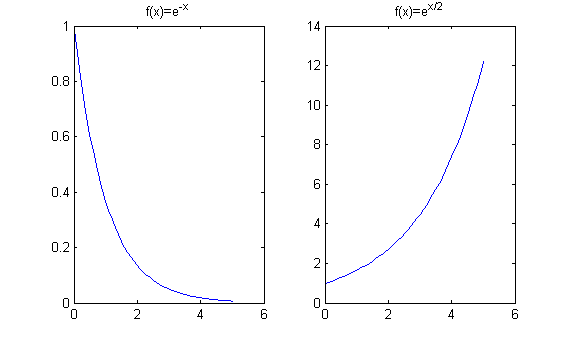
x=0:.1:5;
subplot(1,2,1)
plot(x,exp(-x))
title('f(x)=e^{-x}')
subplot(1,2,2)
plot(x,exp(.5*x))
title('f(x)=e^{x/2}')
Ejercicio 4
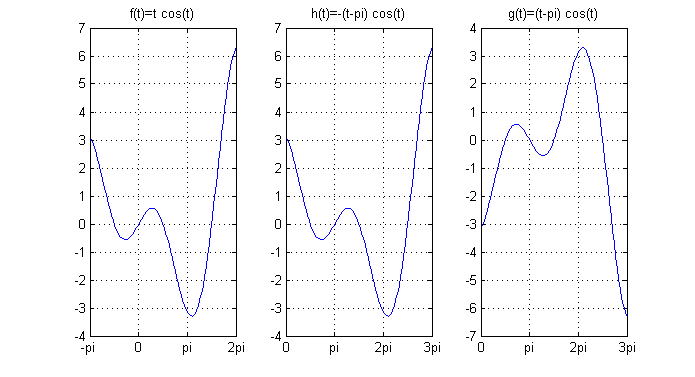
¿Cuál es la relación entre $f(t)=t\cos t$ y $g(t)=(t-\pi)\cos t$?
Solución
Puesto que $\cos(t-\pi)=-\cos(t)$, se tiene que $g(t)=-f(t-\pi)$, es decir, $g(t)$ se obtiene trasladando $\pi$ unidades a la derecha $f(t)$ y haciendo después el opuesto:
Ejercicio 5
¿Cuánto vale la función $f(t)=U(t-1)-U(t-3)$ en $t=2$?
Pista
Solución
Recuerda que $U(t)$ vale cero en $t$ negativo y uno en $t$ positivo.
$f(2)=1$, puesto que en $t=2$, $U(t-1)$ vale $U(1)=1$ y $U(t-3)$ vale $U(-2)=0$. De hecho $f(t)$ vale uno entre $t=1$ y $t=3$ y cero en el resto.
Ejercicio 6
- ¿Hay alguna diferencia entre las siguientes funciones? $$f(t)=U(t-\pi)\,\mbox{sen}\, t \ \ \ \ ,\ \ \ \ g(t)=U(t-\pi)\,\mbox{sen}\, (t-\pi)$$
- Idem para las funciones $$f(t)=U\left(t-\frac{\pi}{2}\right)\, \mbox{sen}\, t \ \ \ \ ,\ \ \ \ g(t)=U\left(t-\frac{\pi}{2}\right)\, \mbox{sen}\left(t-\frac{\pi}{2}\right)$$
Solución
- Sí la hay, $f(t)$ y $g(t)$ son opuestas, ya que $\mbox{sen}\, (t-\pi)=-\mbox{sen}\, t$: $$f(t)=\left\{\begin{array}{lll} 0 & \mbox{si} & t< \pi \\ \mbox{sen}\, t & \mbox{si} & t> \pi \end{array}\right. \hspace{.8cm} \mbox{y} \hspace{.8cm} g(t)=\left\{\begin{array}{lll} 0 & \mbox{si} & t< \pi \\ -\mbox{sen}\, t & \mbox{si} & t> \pi \end{array}\right.$$
- Sí la hay, puesto que $\mbox{sen}(t-\pi/2)=-\cos t$, $$f(t)=\left\{\begin{array}{lll} 0 & \mbox{si} & t< \frac{\pi}{2} \\ \mbox{sen}\, t & \mbox{si} & t> \frac{\pi}{2} \end{array}\right. \hspace{.8cm} \mbox{y} \hspace{.8cm} g(t)=\left\{\begin{array}{lll} 0 & \mbox{si} & t< \frac{\pi}{2} \\ -\cos t & \mbox{si} & t> \frac{\pi}{2} \end{array}\right.$$
Ejercicio 7
Verdadero o falso:
- el número $\int_0^\infty g(t)\, dt$ es el límite de los números $\int_0^b g(t)\, dt$ para $b\rightarrow \infty$
- $\int_0^{\infty} g(s,t)\, dt$ es una función de $s$
- sólo las funciones seccionalmente continuas en $[0,\infty)$ y de orden exponencial admiten transformada de Laplace
Solución
- Verdadero, por definición de integral impropia de primera especie.
- Verdadero
- Falso, eso son condiciones suficientes para la existencia de la transformadas, pero no son necesarias. Por ejemplo, la función $1/\sqrt{t}$ no es seccionalmente continua en $[0,\infty)$ y sin embargo, admite transformada de Laplace.
Ejercicio 8
¿Puede ocurrir que $$I_s=\int_0^{\infty} e^{-st}f(t)\, dt$$ exista y sea finita para $s=0$ y no para $s=1$?¿Y a la inversa?
Pista
Solución
La existencia de esa integral se relaciona con el orden exponencial de la función $f(t)$.
Eso no puede ocurrir; si existe para $s=0$, deberá existir también para cualquier $s>0$. A la inversa sí puede ocurrir.
Ejercicio 9
Sea $F(s)=1/(s-2)={\cal L}[e^{2t}]$. Escribe una integral entre 0 e $\infty$ cuyo valor sea $1$.
Pista
Solución
Utiliza la definición de transformada de Laplace:
$${\cal L}[f(t)]=\int_0^{\infty} e^{-st}f(t)\, dt$$
Puesto que $${\cal L}[e^{2t}]=F(s)=\frac{1}{s-2}=\int_0^{\infty} e^{-st}e^{2t}\, dt$$
tenemos $$1=F(3)=\int_0^{\infty} e^{-3t}e^{2t}\, dt=\int_0^{\infty} e^{-t}\, dt$$
Ejercicio 10
Sabiendo que ${\cal L}[\cos t]=s/(s^2+1)$, para $s>0$, escribe las transformadas de
- $f(t)=e^{-t}\cos t$
- $f(t)=e^{2t}\cos t$
- $f(t)=e^{4t}\cos t$
Pista
Solución
Utiliza la propiedad de traslación en $s$:
$$F(s)={\cal L}[f(t)] \ \mbox{para} \ s>\alpha \hspace{.8cm} \Rightarrow \hspace{.8cm} F(s-a)={\cal L}[e^{at}f(t)] \ \ \ \mbox{para} \ \ s>\alpha+a$$
- $${\cal L}[e^{-t}\cos t]=\frac{s+1}{s^2+2s+2} \hspace{.4cm} \mbox{para} \ \ s>-1$$
- $${\cal L}[e^{2t}\cos t]=\frac{s-2}{s^2-4s+5} \hspace{.4cm} \mbox{para} \ \ s>2$$
- $${\cal L}[e^{4t}\cos t]=\frac{s-4}{s^2-8s+17} \hspace{.4cm} \mbox{para} \ \ s>4$$
>> syms t >> laplace(exp(-t)*cos(t)) ans = (s + 1)/((s + 1)^2 + 1)y representar estas funciones con
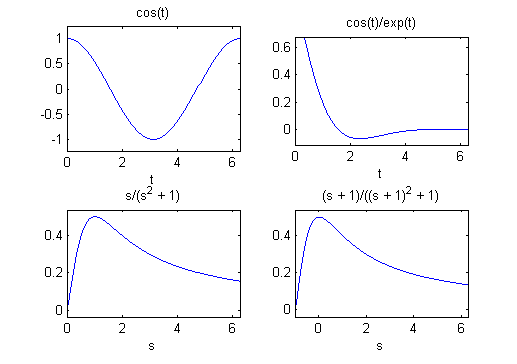
syms t subplot(2,2,1) ezplot(cos(t),[0,2*pi]) subplot(2,2,2) ezplot(exp(-t)*cos(t),[0,2*pi]) subplot(2,2,3) ezplot(laplace(cos(t)),[0,2*pi]) subplot(2,2,4) ezplot(laplace(exp(-t)*cos(t)),[-1,2*pi])
Ejercicio 11
Completa cuadrados en los siguientes polinomios
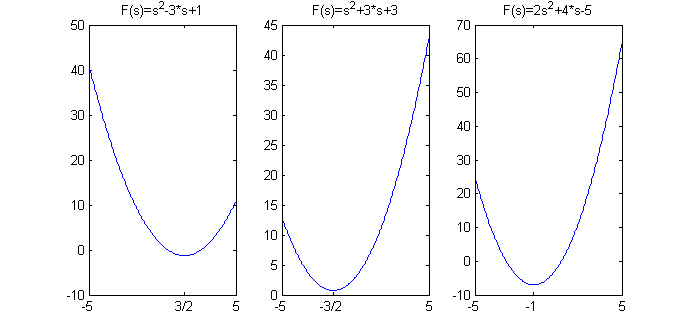
- $s^2-3s+1$
- $s^2+3s+3$
- $2s^2+4s-5$
Solución
- $$s^2-3s+1=\left(s-\frac{3}{2}\right)^2-\frac{5}{4}$$
- $$s^2+3s+3=\left(s+\frac{3}{2}\right)^2+\frac{3}{4}$$
- $$2s^2+4s-5=2(s+1)^2-7$$
s=-5:.05:5;
subplot(1,3,1)
plot(s,s.^2-3*s+1)
set(gca,'XTick',[-5,3/2,5])
set(gca,'XTickLabel',{'-5','3/2','5'})
title('F(s)=s^2-3*s+1')
subplot(1,3,2)
plot(s,s.^2+3*s+3)
set(gca,'XTick',[-5,-3/2,5])
set(gca,'XTickLabel',{'-5','-3/2','5'})
title('F(s)=s^2+3*s+3')
subplot(1,3,3)
plot(s,2*s.^2+4*s-5)
set(gca,'XTick',[-5,-1,5])
set(gca,'XTickLabel',{'-5','-1','5'})
title('F(s)=2s^2+4*s-5')
Ejercicio 12
Sabiendo que ${\cal L}[\mbox{sen}\, bt]=b/(s^2+b^2)$, para $s>0$, escribe las transformadas inversas de
- $$F(s)=\frac{2}{s^2-2s+2} \hspace{.4cm}, \hspace{.4cm} s>1$$
- $$F(s)=\frac{2}{-7+4s-s^2}\hspace{.4cm}, \hspace{.4cm} s>2$$
- $$F(s)=\frac{1}{2s^2+4s+3}\hspace{.4cm}, \hspace{.4cm} s>-1$$
Pista
Solución
Completa cuadrados y utiliza la propiedad de traslación en $s$:
$$F(s)={\cal L}[f(t)] \hspace{.4cm} \mbox{para} \ s>\alpha \hspace{.8cm} \Rightarrow \hspace{.8cm} F(s-a)={\cal L}[e^{at}f(t)] \hspace{.4cm} \mbox{para} \ s>\alpha+a$$
- $${\cal L}^{-1}[F(s)]=2e^t\,\mbox{sen}\, t$$
- b) $${\cal L}^{-1}[F(s)]=-\frac{2}{\sqrt{3}}\, e^{2t}\,\mbox{sen}\, \sqrt{3}t$$
- c) $${\cal L}^{-1}[F(s)]=\frac{1}{\sqrt{2}}\, e^{-t}\,\mbox{sen}\, \frac{t}{\sqrt{2}}$$
>> syms s >> ilaplace(2/(s^2-2*s+2))
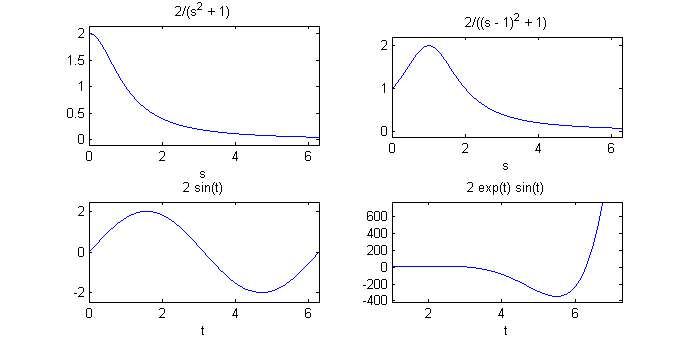
syms s subplot(2,2,1) ezplot(2/(s^2+1),[0,2*pi]) subplot(2,2,2) ezplot(2/((s-1)^2+1),[0,2*pi]) subplot(2,2,3) ezplot(ilaplace(2/(s^2+1)),[0,2*pi]) subplot(2,2,4) ezplot(ilaplace(2/((s-1)^2+1)),[1,2*pi+1])
Ejercicio 13
¿Cuáles de las siguientes funciones se pueden descomponer en fracciones simples?
- $$\frac{2}{s(s+1)}$$
- $$\frac{e^s}{s(s+1)}$$
- $$\frac{\mbox{sen}\, s}{s(s+1)}$$
Solución
Sólo $\frac{2}{s(s+1)}$ puede descomponerse en fracciones simples; las otras no, pues no son funciones racionales (un polinomio dividido entre otro).
Ejercicio 14
Utilizando que ${\cal L}[t^2]=\frac{2}{s^3}$ para $s>0$, escribe las transformadas de
- $f(t)=(t-1)^2U(t-1)$
- $f(t)=5(t-2)^2U(t-2)$
- $f(t)=-(t-3)^2U(t-3)$
Pista
Solución
Utiliza la propiedad de traslación en la variable $t$: si $c$ es un número real positivo,
$${\cal L}[U(t-c)f(t-c)]=e^{-cs}{\cal L}[f(t)]$$
- $${\cal L}[(t-1)^2U(t-1)]=\frac{2}{s^3}\, e^{-s} \ \ \mbox{para} \ \ s>0$$
- $${\cal L}[5(t-2)^2U(t-2)]=\frac{10}{s^3}\, e^{-2s} \ \ \mbox{para} \ \ s>0$$
- $${\cal L}[-(t-3)^2U(t-3)]=-\frac{2}{s^3}\, e^{-3s} \ \ \mbox{para} \ \ s>0$$
>> syms t >> laplace((t-1)^2*heaviside(t-1))y representarlas:
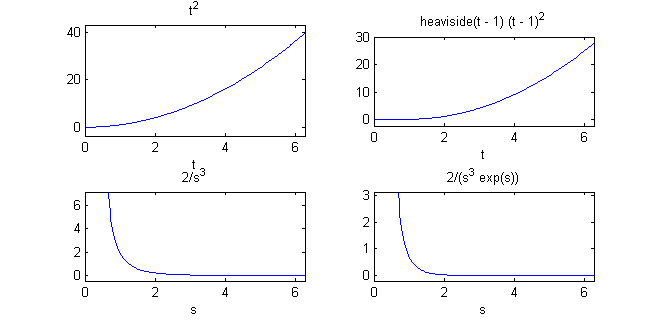
syms t subplot(2,2,1) ezplot(t^2,[0,2*pi]) subplot(2,2,2) ezplot((t-1)^2*heaviside(t-1),[0,2*pi]) subplot(2,2,3) ezplot(laplace(t^2),[0,2*pi]) subplot(2,2,4) ezplot(laplace((t-1)^2*heaviside(t-1)),[0,2*pi])
Ejercicio 15
Utilizando que ${\cal L}[t^n]=n!/s^{n+1}$, para $s>0$ y $n$ natural, escribe las transformadas inversas de
- $$F(s)=\frac{e^{-2s}}{s^2} \hspace{.4cm}, \hspace{.4cm} s>0$$
- $$F(s)=\frac{e^{-s}}{s^3}\hspace{.4cm}, \hspace{.4cm} s>0$$
- $$F(s)=\frac{e^{-3s}}{s^4}\hspace{.4cm}, \hspace{.4cm} s>0$$
Pista
Solución
Utiliza la propiedad de traslación en la variable $t$: si $c$ es un número real positivo,
$${\cal L}[U(t-c)f(t-c)]=e^{-cs}{\cal L}[f(t)]$$
- puesto que ${\cal L}^{-1}[1/s^2]=t$ $${\cal L}^{-1}[F(s)]=(t-2)U(t-2)$$
- puesto que ${\cal L}^{-1}[1/s^3]=t^2/2$ $${\cal L}^{-1}[F(s)]=\frac{1}{2}(t-1)^2U(t-1)$$
- puesto que ${\cal L}^{-1}[1/s^4]=t^3/6$ $${\cal L}^{-1}[F(s)]=\frac{1}{6}(t-3)^3U(t-3)$$
>> syms s
>> ilaplace(exp(-s)/s^3)
ans =
(heaviside(t - 1)*(t - 1)^2)/2
y podemos dibujar las funciones transformadas y sus inversas:
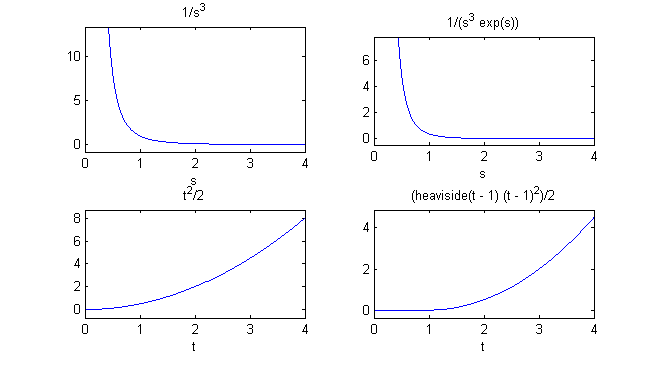
subplot(2,2,1) ezplot(1/s^3,[0,4]) subplot(2,2,2) ezplot(exp(-s)/s^3,[0,4]) subplot(2,2,3) ezplot(ilaplace(1/s^3),[0,4]) subplot(2,2,4) ezplot(ilaplace(exp(-s)/s^3),[0,4])
Ejercicio 16
Si $f$ y $g$ son funciones definidas únicamente en el semieje positivo, ¿Cuáles de las siguientes funciones son $f*g(t)$?
- $\int_0^tf(u)\, g(u-t)\, du$
- $\int_0^tf(u)\, g(t-u)\, dt$
- $\int_0^tf(u)\, g(t-u)\, du$
- $\int_{-t}^tf(x)\, g(t-x)\, dx$
- ${\cal L}^{-1}[{\cal L}[f]{\cal L}[g]](t)$
Solución
- No lo es;
- No lo es, pues no es correcta la variable de integración;
- Ésta sí es la convolución de $f(t)$ con $g(t)$
- No lo es, es incorrecto el intervalo de integración;
- Ésta sí es la convolución de $f(t)$ con $g(t)$, en base a la propiedad de la transformada de Laplace de la convolución: la transformada de la convolución es el producto de las transformadas.
Ejercicio 17
Utilizando que ${\cal L}[\delta^{(n}(t)]=s^n$, $n=0,\, 1,\,\ldots$ encuentra la inversa de
- $F(s)=s^3+2s^2-s+5$
- $F(s)=s^4-3$
- $F(s)=s^3-3s$
Solución
Debido a la linealidad,
- $${\cal L}^{-1}[s^3+2s^2-s+5]=\delta'''(t)+2\delta''(t)-\delta'(t)+5\delta(t)$$
- $${\cal L}^{-1}[s^4-3]=\delta^{(4}(t)-3\delta(t)$$
- $${\cal L}^{-1}[s^3-3s]=\delta'''(t)-3\delta'(t)$$
Ejercicio 18
Escribe, utilizando la función generalizada Delta de Dirac, las derivadas respecto de $t$ de
- $U(t-1)$
- $U(2-t)$
- $U'(t-3)$
Pista
Solución
Recuerda que $\frac{d}{dt}U(t)=\delta(t)$ y observa que $U(a-t)=1-U(t-a)$
- $$\frac{d}{dt}U(t-1)=\delta(t-1)$$
- $$\frac{d}{dt}U(2-t)=-\delta(t-2)$$
- $$\frac{d^2}{dt^2}U(t-3)=\delta'(t-3)$$
Ejercicio 19
Opera:
- $t\,\delta(t-3)$
- $(t^2-1)\,\delta(t)$
- $\delta(t)\,\cos t$
- $\delta(t-\pi)\,\cos t$
Pista
Solución
Utiliza que si $f(t)$ es continua en $t=t_0$,
$$\delta(t-t_0)f(t)=f(t)\delta(t-t_0)=f(t_0)\delta(t-t_0)$$
- $t\,\delta(t-3)=3\delta(t-3)$ ya que $f(t)=t$ es continua en $t=3$
- $(t^2-1)\,\delta(t)=-\delta(t)$ ya que $f(t)=t^2-1$ es continua en $t=0$
- $\delta(t)\,\cos t=\delta(t)$ ya que $f(t)=\cos t$ es continua en $t=0$
- $\delta(t-\pi)\,\cos t=-\delta(t-\pi)$ ya que $f(t)=\cos t$ es continua en $t=\pi$
Ejercicio 20
Expresa las siguientes funciones generalizadas en función de $\delta(t)$:
- $\delta(2t)$
- $\delta(-4t)$
- $\delta(t/10)$
Pista
Solución
Recuerda que $$\delta(at)=\frac{1}{|a|}\delta(t)$$
- $\delta(2t)=\delta(t)/2$
- $\delta(-4t)=\delta(t)/4$
- $\delta(t/10)=10\delta(t)$
Ejercicio 21
Halla la función de transferencia de las siguientes ecuaciones
- $y''+2y'-y=0$
- $y''+2y'=U(t)$
- $y''-3y=\delta(t)$
Pista
Solución
La función de transferencia de la ecuación diferencial $ay''+by'+cy=g(t)$ es la función $$H(s)=\frac{1}{as^2+bs+c}$$
- $$H(s)=\frac{1}{s^2+2s-1}$$
- $$H(s)=\frac{1}{s^2+2s}$$
- $$H(s)=\frac{1}{s^2-3}$$